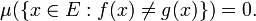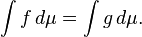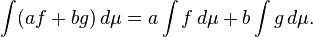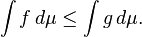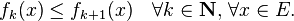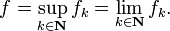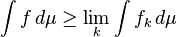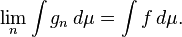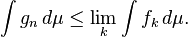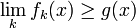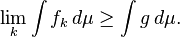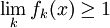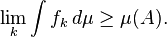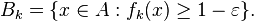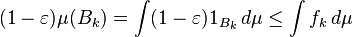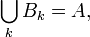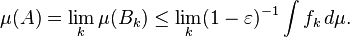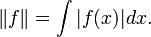Integración de Lebesgue
Antecedentes
SOS Children produjo este sitio web para las escuelas, así como este sitio web video sobre África . Haga clic aquí para obtener información sobre el apadrinamiento de niños.
En las matemáticas , la integral de un no negativo función puede ser considerada en el caso más sencillo como el área entre el . gráfica de esa función y la integración eje x Lebesgue es una construcción matemática que se extiende la integral a una clase más amplia de funciones; sino que también se extiende a la dominios en los que estas funciones se pueden definir. Desde hace tiempo se había entendido que para que las funciones no negativas con un gráfico lo suficientemente suave (tal como funciones continuas en cerrado delimitada intervalos) el área bajo la curva se podrían definir como la integral y calculan utilizando técnicas de aproximación de la región por polígonos . Sin embargo, como la necesidad de considerar las funciones más irregulares surgió (por ejemplo, como resultado de las limitantes procesos de análisis matemático y la matemática teoría de la probabilidad ) se hizo evidente que serían necesarias técnicas de aproximación más cuidadosas para definir una integral adecuado. También, puede ser que deseen integrar en espacios más generales de la línea real; la integral de Lebesgue ofrece las abstracciones correctas necesarias para realizar este importante trabajo.
La integral de Lebesgue juega un papel importante en la rama de las matemáticas llamado análisis real y en muchos otros campos de las ciencias matemáticas, y lleva el nombre de Henri Lebesgue (1875-1941) quien introdujo la integral en (Lebesgue 1904). También es una parte fundamental de la teoría axiomática de la probabilidad.
El término "integración Lebesgue" puede referirse tanto a la teoría general de la integración de una función con respecto a un general medir, introducido por Lebesgue, o para el caso específico de la integración de una función definida en un subdominio de la recta real con respecto a Medida de Lebesgue.
Introducción
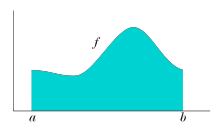
La integral de una función f entre los límites A y B puede ser interpretado como el área bajo la gráfica de f. Esto es fácil de entender para las funciones familiares como polinomios , pero ¿qué significa para las funciones más exóticos? En general, ¿cuál es la clase de funciones para las que "área bajo la curva" tiene sentido? La respuesta a esta pregunta tiene una gran importancia teórica y práctica.
Como parte de un movimiento general hacia rigor en las matemáticas en el siglo XIX, hubo intentos de poner el cálculo integral sobre una base firme. La Integral de Riemann, propuesta por Bernhard Riemann (1826-1866), es un intento ampliamente adjudicatario la constitución de una fundación tal. La definición de Riemann comienza con la construcción de una secuencia de áreas calculadas fácilmente que convergen a la integral de una función dada. Esta definición tiene éxito en el sentido de que da la respuesta esperada para muchos problemas ya resueltos-y da resultados útiles para muchos otros problemas.
Sin embargo, la integración de Riemann no interactúa bien con la toma de límites de secuencias de funciones, por lo que tales procesos limitantes difíciles de analizar. Esto es de importancia primordial, por ejemplo, en el estudio de Series de Fourier, Transformadas de Fourier y otros temas. La integral de Lebesgue es más capaz de describir cómo y cuándo es posible tomar límites bajo el signo integral. La definición de Lebesgue considera una clase diferente de áreas calculadas fácilmente que la definición de Riemann, que es la razón principal por la integral de Lebesgue un mejor comportamiento. La definición de Lebesgue también hace que sea posible calcular las integrales para una clase más amplia de funciones. Por ejemplo, el Función de Dirichlet, que es 0 en su argumento es irracional y 1 en caso contrario, tiene una integral de Lebesgue, pero no tiene una integral de Riemann.
El enfoque de Lebesgue de integración se resumió en una carta a Paul Montel. Él escribe:
Tengo que pagar una cierta suma, que he recogido en mi bolsillo. Tomo los billetes y monedas de mi bolsillo y les doy a los acreedores en el orden los encuentro hasta que haya alcanzado la suma total. Esta es la integral de Riemann. Pero puedo proceder de manera diferente. Después he tomado todo el dinero de mi bolsillo ordeno los billetes y monedas de acuerdo con valores idénticos y luego tengo que pagar los varios montones, uno tras otro al acreedor. Este es mi integral.- Fuente: (Siegmund-Schultze 2008)
La idea es que uno debe ser capaz de reorganizar los valores de una función libremente preservando al mismo tiempo el valor de la integral. Este proceso de reordenación puede convertir una función muy patológica en una que es "agradable" desde el punto de vista de la integración, y por lo tanto permite tales funciones patológicas que se integra.
Interpretación intuitiva

Para tener una intuición sobre los diferentes enfoques de la integración, imaginemos que se desea encontrar el volumen de una montaña (sobre el nivel del mar).
- El enfoque de Riemann-Darboux
- Divida la base de la montaña en una rejilla de cuadrados de 1 metro. Mida la altura de la montaña en el centro de cada cuadrado. El volumen en un solo cuadrado de la cuadrícula es de aproximadamente 1 × 1 × (altitud), de modo que el volumen total es la suma de las altitudes.
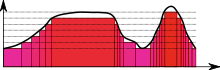
- El enfoque de Lebesgue
- Dibuja un mapa de contorno de la montaña, donde los contornos adyacentes son de 1 metro de altura de diferencia. El volumen de la tierra contenida en un solo contorno es de aproximadamente veces zona de contorno que 1, por lo que el volumen total es la suma de estas áreas veces 1 metro.
Folland resume la diferencia entre el Riemann y Lebesgue enfoques así: "para calcular la integral de Riemann de f, uno particiones del dominio [a, b] en subintervalos", mientras que en la integral de Lebesgue, "uno es, en efecto, la partición de la gama de f ".
Hacia una definición formal
Para definir la integral de Lebesgue requiere formalmente la noción de un medida que, más o menos, asocia a cada conjunto A de los números reales no negativos un número μ (A) que representan el "tamaño" de A. Esta noción de "tamaño" debe estar de acuerdo con la duración habitual de una unión de intervalos o disjuntos de intervalos. Supongamos que f: R → R es una función real no negativo. Uso de la "partición de la gama de f" la filosofía, la integral de f debe ser la suma sobre t de las áreas entre una franja horizontal fina entre y = t y y = t + dt. Esta área es sólo
Dejar
La integral de Lebesgue de f se define entonces por
donde la integral de la derecha es un ordinario inadecuada integral de Riemann (obsérvese que f * es una función positiva estrictamente decreciente, y por lo tanto tiene una inadecuada Riemann bien definida integral). Para una clase adecuada de funciones (la funciones medibles) Esto define la integral de Lebesgue.
Un general (no necesariamente positivo) la función f es integrable Lebesgue si el área entre la gráfica de f y el eje x es finito:
En ese caso, la integral es, como en el caso de Riemann, la diferencia entre el área por encima del eje x y el área debajo del eje x:
donde
Construcción
La discusión que sigue paralela a la expositivo enfoque más común a la integral de Lebesgue. En este enfoque, la teoría de la integración tiene dos partes distintas:
- Una teoría de conjuntos medibles y medidas sobre estos conjuntos.
- Una teoría de funciones medibles e integrales sobre estas funciones.
La función cuya integral se encuentra a continuación, se aproxima por cierto la llamada funciones simples, cuyas integrales puede escribirse en términos de la medida. La integral de la función original es entonces el límite de la integral de las funciones simples.
Teoría de la medida
Teoría de la medida fue creada inicialmente para proporcionar una abstracción útil de la noción de longitud de subconjuntos de la recta real y, más en general, área y volumen de subconjuntos de espacios euclídeos. En particular, se proporciona una respuesta sistemática a la cuestión de que los subconjuntos de R tienen una longitud. Como se ha demostrado por los acontecimientos posteriores en la teoría de conjuntos (véase conjunto no medible), en realidad es imposible asignar una longitud de todos los subconjuntos de R de una manera que conserva algunos de aditividad y la traducción de invariancia propiedades naturales. Esto sugiere que la selección de un clase adecuada de subconjuntos medibles es un requisito esencial.
La integral de Riemann utiliza la noción de longitud de forma explícita. De hecho, el elemento de cálculo de la integral de Riemann es el rectángulo [a, b] × [c, d], cuya área se calcula que (b - a) (d - c). La cantidad b - a es la longitud de la base del rectángulo y d - c es la altura del rectángulo. Riemann sólo podía utilizar rectángulos planos para aproximar el área bajo la curva, porque no había una teoría adecuada para la medición de los conjuntos más generales.
En el desarrollo de la teoría en la mayoría de los libros de texto modernos (después de 1950), el enfoque para medir y la integración es axiomático. Esto significa que una medida es cualquier función μ definida en un cierto X clase de subconjuntos de un conjunto E, que satisface una cierta lista de propiedades. Estas propiedades se pueden mostrar para mantener en muchos casos diferentes.
Integración
Empezamos con una espacio de medida (E, X, μ) donde E es un conjunto , X es una σ-álgebra de subconjuntos de E y μ es una (no negativo) medir en E, definido en los sets de X.
Por ejemplo, E puede ser euclidiano n-espacio R n o algún Lebesgue subconjunto medible de la misma, será el X. σ-álgebra de todos los subconjuntos medibles Lebesgue de E y μ será el Medida de Lebesgue. En la teoría matemática de la probabilidad, nos limitamos nuestro estudio a una probabilidad medida μ, que satisface μ (E) = 1.
En la teoría de Lebesgue, integrales se definen para una clase de funciones llamado funciones medibles. Una función f es medible si el pre-imagen de cada intervalo de la forma (t, ∞) está en X:
Se puede demostrar que esto es equivalente a requerir que el pre-imagen de cualquier Borel subconjunto de R sea en X. Vamos a hacer esta suposición en adelante. El conjunto de funciones medibles es cerrado bajo las operaciones algebraicas, pero lo más importante de la clase se cierra bajo diversos tipos de Pointwise límites secuenciales:
se pueden medir si el k secuencia original (f k), donde k ∈ N, se compone de funciones medibles.
Construimos una integral
para funciones reales medibles f definida en E en etapas:
Indicador Funciones: Para asignar un valor a la integral de la función indicadora 1 S de un conjunto S medible en consonancia con la medida dada μ, la única opción razonable es establecer:
Observe que el resultado puede ser igual a + ∞, a menos que μ es una medida finita.
Funciones simples: Un finito combinación lineal de funciones de los indicadores
donde los coeficientes a k son números reales y los conjuntos S k son medibles, que se llama una medible función simple. Extendemos la integral de linealidad para funciones simples medibles no negativas. Cuando los coeficientes a k no son negativos, establecemos
La convención 0 × ∞ = 0 debe ser utilizado, y el resultado puede ser infinita. Incluso si una función simple se puede escribir de muchas maneras como una combinación lineal de las funciones del indicador, la integral será siempre el mismo; esto se puede demostrar mediante la propiedad de aditividad de las medidas.
Se necesita un cierto cuidado al definir la integral de una función simple de valor real, para evitar la expresión indefinida ∞ - ∞: Se supone que la representación
es tal que μ (S k) <∞ cada vez que un k ≠ 0. Entonces la fórmula anterior para la integral de f tiene sentido, y el resultado no depende de la representación particular de f satisfacer los supuestos.
Si B es un subconjunto medible de E y s es una función simple medible uno define
Las funciones no negativas: Sea f una función medible no negativa en E que permitimos que para alcanzar el valor + ∞, es decir, f toma valores no negativos en la extendida recta numérica real. Definimos
Tenemos que mostrar esto coincide integrales con la anterior, definida en el conjunto de funciones simples. Cuando E es un segmento [a, b], existe también la cuestión de si esto corresponde en modo alguno a una noción de Riemann de la integración. Es posible demostrar que la respuesta a ambas preguntas es sí.
Hemos definido la integral de f para cualquier función real extendida no negativo mensurable en E. Para algunas funciones, esta integral ∫ E f dμ será infinito.
Funciones Firmado: Para manejar las funciones firmados, necesitamos un poco más de las definiciones. Si f es una función medible de la serie E para los reales (incluyendo ± ∞), entonces podemos escribir
donde
Tenga en cuenta que tanto f + f - son funciones medibles no negativas. También tenga en cuenta que
Decimos que existe la integral de Lebesgue de la función medible f, o se define si al menos uno de 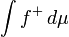 y
y 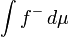 es finito:
es finito:
En este caso definimos
Si
decimos que f es integrable Lebesgue.
Resulta que esta definición da las propiedades deseables de la integral.
Complejas funciones con valores pueden ser integrados de manera similar, teniendo en cuenta la parte real y la parte imaginaria por separado.
Ejemplo
Considera el función de indicador de los números racionales, 1 Q. Esta función es ninguna parte continua.
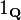 No es-Riemann integrable en [0,1]: No importa cómo se reparte el conjunto [0,1] en subintervalos, cada partición contiene al menos un racional y al menos un número irracional, porque los racionales y los irracionales son a la vez denso en los reales. Por lo tanto la parte superior Sumas Darboux todos serán uno, y las sumas inferiores Darboux todos serán cero.
No es-Riemann integrable en [0,1]: No importa cómo se reparte el conjunto [0,1] en subintervalos, cada partición contiene al menos un racional y al menos un número irracional, porque los racionales y los irracionales son a la vez denso en los reales. Por lo tanto la parte superior Sumas Darboux todos serán uno, y las sumas inferiores Darboux todos serán cero.
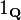 es Lebesgue integrable en [0,1] con la Medida de Lebesgue: De hecho, es la función indicadora de los racionales así por definición
es Lebesgue integrable en [0,1] con la Medida de Lebesgue: De hecho, es la función indicadora de los racionales así por definición
- porque Q es contable.
Dominio de la integración
Un problema técnico en la integración de Lebesgue es que el dominio de la integración se define como un conjunto (un subconjunto de un espacio de medida), sin noción de orientación. En cálculo elemental, se define la integración con respecto a una Orientación:
Generalizando esta a las dimensiones mayores rendimientos integración de formas diferenciales. Por el contrario, la integración de Lebesgue proporciona una generalización alternativa, integrando sobre subconjuntos con respecto a una medida; esto puede ser anotada como
para indicar integración sobre un subconjunto A. Para más detalles sobre la relación entre estas generalizaciones, consulte Forma diferencial: Relación con las medidas.
Limitaciones de la integral de Riemann
Aquí hablamos de las limitaciones de la integral de Riemann y el mayor alcance que ofrece la integral de Lebesgue. Partimos de una comprensión de trabajo de la Integral de Riemann.
Con el advenimiento de Series de Fourier, muchos problemas analíticos relacionados con las integrales acercó cuya solución satisfactoria requiere intercambiar procesos límite y signos integrales. Sin embargo, las condiciones en que las integrales
son iguales resultó bastante difícil de alcanzar en el marco de Riemann. Hay algunas otras dificultades técnicas con la integral de Riemann. Estos están vinculados con la dificultad límite de toma discutido anteriormente.
El fallo de la convergencia monótona. Como se muestra anteriormente, la función indicadora 1 Q en los racionales no es Riemann integrable. En particular, la Teorema de la convergencia monótona falla. Para ver por qué, sea {k} una enumeración de todos los números racionales en [0,1] (que son contable así que esto se puede hacer.) Luego deje
La función g k es cero en todas partes excepto en un conjunto finito de puntos, de ahí su integral de Riemann es cero. La secuencia de g k también es claramente no negativo y monótonamente creciente a 1 Q, que no es Riemann integrable.
Inadecuación para intervalos no acotados. La integral de Riemann sólo puede integrar las funciones en un intervalo acotado. Sin embargo, puede extenderse a intervalos no acotados tomando límites, siempre y cuando esto no da una respuesta como ∞-∞.
La integración en las estructuras distintas de espacio euclidiano. La integral de Riemann está inextricablemente ligada a la estructura de orden de la línea.
Teoremas básicos de la integral de Lebesgue
La integral de Lebesgue no distingue entre las funciones que difieren sólo en un conjunto de μ-medida cero. Para hacer esta precisión, funciones f y g se dice que son iguales en casi todas partes (ae) si
- Si f, g son funciones medibles no negativas (posiblemente asumiendo el valor + ∞) tal que f = g en casi todas partes, a continuación,
A saber, la integral respeta la relación de equivalencia de casi todas partes la igualdad.
- Si f, g son funciones tales que f = g en casi todas partes, entonces f es integrable Lebesgue si y sólo si g es integrable Lebesgue, y las integrales de f y g son los mismos si es que existen.
La integral de Lebesgue tiene las siguientes propiedades:
Linealidad: Si fyg son funciones integrables Lebesgue y a y b son números reales, entonces af + bg es Lebesgue integrable y
Monotonía: Si f ≤ g, a continuación,
Monótono teorema de convergencia: Supongamos que {f k} k ∈ N es una secuencia de funciones medibles no negativas de tal manera que
Entonces, el límite puntual f de f k es Lebesgue integrable y
Nota: El valor de cualquiera de las integrales se le permite ser infinito.
Lema de Fatou: Si {f k} k ∈ N es una secuencia de funciones medibles no negativas, entonces
Una vez más, el valor de cualquiera de las integrales puede ser infinita.
Teorema de convergencia dominada: Supongamos {f k} k ∈ N es una secuencia de complejas funciones medibles con límite de punto a punto f, y no es una función integrable Lebesgue g (es decir, g pertenece a la espacio L 1) tal que | f k | ≤ g para todo k.
Entonces, f es integrable Lebesgue y
Técnicas de prueba
Para ilustrar algunas de las técnicas que se empleen en la teoría de la integración de Lebesgue, esbozamos una prueba de la mencionada Lebesgue convergencia monótona teorema. Sea {f k} k ∈ N es una secuencia no decreciente de funciones medibles no negativas y poner
Por la propiedad de monotonicidad de la integral, es inmediato que:
y existe el límite de la derecha, porque la sucesión es monótona. Ahora probaremos la desigualdad en la otra dirección. Se desprende de la definición de integral que hay una secuencia no decreciente (g n) de funciones simples no negativos tales que g n ≤ f y
Por lo tanto, es suficiente para probar que para cada n ∈ N,
Vamos a demostrar que si g es una función simple y
casi en todas partes, a continuación,
Al romper la función g en sus partes de valor constante, esto reduce al caso en el que g es la función indicadora de un conjunto. El resultado tenemos que demostrar es entonces
Supongamos que A es un conjunto medible y {f k} k ∈ N es una secuencia no decreciente de funciones medibles no negativas en E tal que
para casi todo x ∈ A. Entonces
Para demostrar este resultado, fijar ε> 0 y definir la secuencia de conjuntos medibles
Por monotonicidad de la integral, se deduce que para cualquier k ∈ N,
Debido a que casi todo x estarán en B k para k suficientemente grande, tenemos
hasta un conjunto de medida 0. Así por aditividad numerable de μ, y porque B k aumenta con k,
Como esto es cierto para cualquier ε positivo el resultado sigue.
Formulaciones alternativas
Es posible desarrollar la integral con respecto a la medida de Lebesgue sin depender de la maquinaria completa de teoría de la medida. Uno de tales enfoques es proporcionada por el Daniell integral.
También hay un enfoque alternativo para el desarrollo de la teoría de la integración a través de métodos de análisis funcional. Existe la integral de Riemann para cualquier función f continua de soporte compacto definido en R n (o un subconjunto abierto fijo). Integrales de funciones más generales se pueden construir a partir de estas integrales.
Sea C C el espacio de todas las funciones continuas con soporte compacto con valores reales de R. Definir una norma en C c por
Entonces C c es un espacio vectorial normado (y, en particular, es un espacio métrico.) Todos los espacios métricos tienen Terminaciones Hausdorff, así que vamos L1 ser su finalización. Este espacio es isomorfo al espacio de funciones integrables Lebesgue modulo el subespacio de funciones con cero integral. Además, la integral ∫ Riemann es una uniformemente continua funcional con respecto a la norma en C c, que es denso en L 1. Por lo tanto ∫ tiene una extensión única para todos L1. Esta integral es precisamente la integral de Lebesgue.
Más generalmente, cuando el espacio de medida en la que se definen las funciones es también una localmente compacto espacio topológico (como es el caso con los números reales R), las medidas compatibles con la topología en un sentido adecuado ( Medidas de Radon, de los cuales la medida de Lebesgue es un ejemplo) una integral con respecto a ellos se pueden definir de la misma manera, a partir de las integrales de funciones continuas con soporte compacto. Más precisamente, las funciones de soporte compacto forman un espacio vectorial que lleva un naturales topología, y un (radón) medida se define como un continuo funcional lineal en este espacio. El valor de una medida en una función de soporte compacto es entonces también, por definición, la integral de la función. Uno procede entonces para expandir la medida (la integral) a las funciones más generales por la continuidad, y define la medida de un conjunto como la integral de la función de indicador. Este es el enfoque adoptado por Bourbaki (2004) y un cierto número de otros autores. Para más detalles ver Medidas de Radon.
Limitaciones de la integral de Lebesgue
El objetivo principal de integral de Lebesgue es proporcionar una notación integral donde los límites de integrales tienen bajo supuestos leves. No hay garantía de que cada función es integrable Lebesgue. Puede suceder que existen (Riemann) integrales impropias de funciones que no son de Lebesgue integrable. Un ejemplo sería
Esta función no es integrable Lebesgue como
Por otra parte, existe como una inadecuada integral de Riemann y la integral se puede calcular para ser finito. Un concepto equivalente de integral impropia Lebesgue no existe porque la perspectiva es innecesaria desde el punto de vista de los teoremas de convergencia.
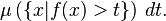
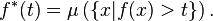
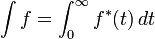
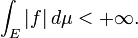
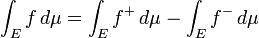

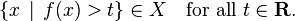
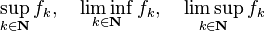
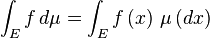
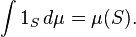
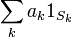
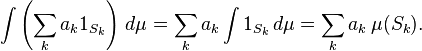
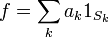
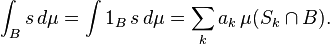
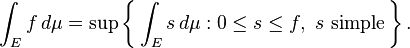
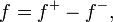
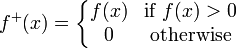
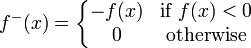
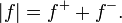

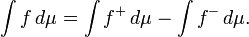
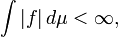
![\ Int _ {[0,1]} 1 _ {\ mathbf Q} \, d \ mu = \ mu (\ mathbf {Q} \ cap [0,1]) = 0,](../../images/2452/245211.png)
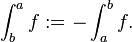
![\ Int_a f \, d \ mu = \ int _ {[a, b]} f \, d \ mu](../../images/2452/245213.png)
![\ Sum_k \ int f_k (x) dx, \ quad \ int \ left [\ sum_k f_k (x) \ right] dx](../../images/2452/245214.png)