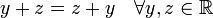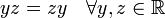Propriedade comutativa

Exemplo mostrando a commutativity de adição (+ 2 3 + 2 = 3)

Comutatividade é amplamente utilizado matemático termo que se refere a capacidade de alterar a ordem dos algo sem alterar o resultado final. É uma propriedade fundamental na maioria dos ramos da matemática e muitas provas dependem dele. A comutatividade das operações simples foi durante muitos anos implicitamente assumidos ea propriedade não foi dado um nome ou atribuídos até o século 19, quando os matemáticos começaram a formalizar a teoria da matemática.

Os usos mais comuns

A propriedade comutativa (ou lei comutativa) é uma propriedade associada operações e binários funções . Da mesma forma, se a propriedade conmutativo prende por um par de elementos sob uma certa operação de binário então diz-se que os dois elementos comutar sob essa operação.

Em grupo e teoria dos conjuntos , muitas estruturas algébricas são chamados comutativa quando certas operandos satisfazer a propriedade comutativa. Em ramos mais altos de matemática, tais como análise e álgebra linear a comutatividade das operações bem conhecidas (como adição e multiplicação com números reais e complexos) é frequentemente utilizado (ou implicitamente) em provas.

Definições matemáticas

O termo "conmutativo" é usado em vários sentidos relacionados.

1. Um operação binária * em um conjunto S é dito ser comutativa se:

x * y = x * y para cada x, y ∈ S

• Uma operação que não satisfaz a propriedade acima é chamado de não-comutativa.

2. Diz-se que x comuta com y sob * se:

x * y = x y *

3. Um função binária F: A X A → B é dito ser conmutativo se:

f (x, y) = f (y, x) para cada x, y ∈ A.

História e etimologia

O primeiro uso conhecido do termo foi em um jornal francês publicou em 1814

Registros do uso implícito da propriedade comutativa voltar aos tempos antigos. Os egípcios usaram a propriedade comutativa da multiplicação para simplificar a computação produtos. Euclides é conhecido por ter assumido a propriedade comutativa da multiplicação em seu livro Elements . Usos formais da propriedade comutativa surgiu no final dos anos 18 e início do século 19, quando os matemáticos começaram a trabalhar em uma teoria de funções. Hoje a propriedade comutativa é uma propriedade bem conhecida e básico usado na maioria dos ramos da matemática. Versões simples da propriedade comutativa são normalmente ensinadas em cursos de matemática começando.

O primeiro uso do termo comutativa real estava em um livro de memórias por Francois Servois em 1814, que usou a palavra commutatives quando descrevendo as funções que têm o que é chamado agora a propriedade comutativa. A palavra é uma combinação da palavra francesa suburbano significado "para substituir ou interruptor" eo significado -ative sufixo "tende a" assim que a palavra significa literalmente "que tende a substituir ou interruptor." O termo, em seguida, apareceu em Inglês Philosophical Transactions, da Royal Society em 1844.

Propriedades relacionadas

Gráfico mostrando a simetria da função de adição

Associatividade

A associatividade está intimamente relacionado com a propriedade comutativa. A propriedade associativa afirma que a ordem em que as operações são executadas não afectam o resultado final. Em contraste, a propriedade conmutativo afirma que a ordem dos termos não afectam o resultado final.

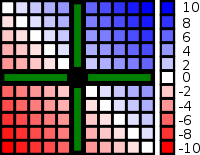
Simetria

Simetria pode ser diretamente ligado a comutatividade. Quando um operador conmutativo está escrito como uma função binária, em seguida, a função resultante é simétrica do outro lado da linha y = x. Como um exemplo, se permitirmos que uma função f representam adição (uma operação conmutativo) de modo a que f (x, y) = x + y então f é uma função simétrica, que pode ser visto na imagem do lado direito.

Exemplos

Operações comutativos na vida cotidiana

• Colocar seus sapatos se assemelha a uma operação comutativa, uma vez que não importa se você colocar o sapato esquerdo ou direito em primeiro lugar, o resultado final (tendo ambos os sapatos), é o mesmo.
• Ao fazer a mudança que nós aproveitar a comutatividade de adição. Não importa que ordem vamos colocar a mudança em, ele sempre acrescenta ao mesmo total.

Operações comutativos em matemática

Exemplo mostrando a comutatividade da multiplicação (3 * 5 * 5 = 3)

Dois exemplos bem conhecidos de operações binárias comutativos são:

• A adição de números reais , que é comutativa desde

Por exemplo 4 + 5 + = 5 4, uma vez que ambos expressões igual 9.

• A multiplicação de números reais , que é comutativa desde

Por exemplo, 3 × 5 × 5 = 3, uma vez que ambas as expressões igual a 15.

• Outros exemplos de operações binárias comutativos incluem adição e multiplicação de números complexos , a adição de vetores , e interseção e união de conjuntos.

Operações Noncommutative na vida cotidiana

Concatenação, o ato de unir cadeias de caracteres juntos, é uma operação comutativa.

• Lavar e secar suas roupas se assemelha a uma operação comutativa, se você seca primeiro e depois lavar, você obtém um resultado significativamente diferente do que se você lavar primeiro e depois seco.
• O Cubo de Rubik é não-comutativa. Por exemplo, torcendo o horário face frontal, a parte superior dos ponteiros do relógio rosto e da face frontal esquerda (FUF ') não produz o mesmo resultado que torcer o rosto no sentido horário da frente, em seguida, sentido anti-horário e, finalmente, torcer o topo no sentido horário (FF'U). As voltas não comutar. Este é estudada em teoria de grupos .

Noncommutative operações em matemática

Algumas operações binárias não comutativos são:

• subtração é comutativa desde
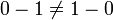
• divisão é não-comutativa desde
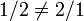
• matriz de multiplicação é comutativa desde

As estruturas matemáticas e comutatividade

• Um grupo abeliano é um grupo cujo funcionamento grupo é comutativa.
• Um anel comutativo é um anel cuja multiplicação é comutativa. (Adição de um anel é, por definição, sempre comutativa.)
• Em um campo tanto adição e multiplicação são comutativa.
• O centro é o maior subconjunto comutativo de um grupo.