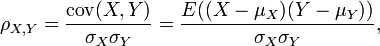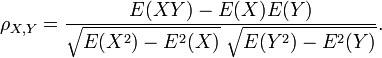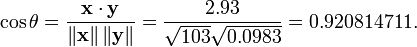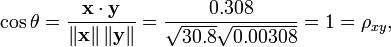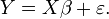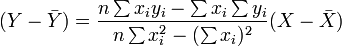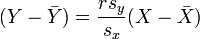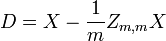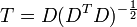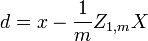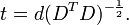Correlação

Assuntos Relacionados: Matemática

Você sabia ...

SOS acredita que a educação dá uma chance melhor na vida de crianças no mundo em desenvolvimento também. Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.

Este artigo é sobre o coeficiente de correlação entre duas variáveis. A correlação termo também pode significar a cross-correlação de duas funções ou correlação de elétrons em sistemas moleculares.

Vários conjuntos de (x, y) pontos, com o coeficiente de correlação de x e y para cada conjunto. Note-se que a correlação reflete o noisiness e direção de uma relação linear (linha superior), mas não a inclinação dessa relação (meio), nem muitos aspectos de relações não-lineares (em baixo). NB: a figura no centro tem uma inclinação de 0, mas, nesse caso, o coeficiente de correlação é indefinido pois a variância de Y é zero.

Em teoria da probabilidade e estatísticas , correlação, (muitas vezes medida como um coeficiente de correlação), indica a força ea direção de uma relação linear entre duas variáveis aleatórias . No uso estatístico geral, correlação ou co-relação refere-se à partida de duas variáveis de independência. Neste sentido lato, há diversos coeficientes, medindo o grau de correlação, adaptados à natureza dos dados.

Um número de coeficientes diferentes são usadas para situações diferentes. O mais conhecido é o Coeficiente de correlação de Pearson, que é obtido através da divisão do covariância das duas variáveis com o produto dos seus desvios padrão . Apesar do nome, que foi introduzido pela primeira vez por Francis Galton.

Coeficiente de produto-momento de Pearson

Propriedades matemáticas

O coeficiente de correlação ρ _{X, Y} entre duas variáveis aleatórias X e Y com valores esperados μ _X e _Y μ e desvio padrão σ _X e _Y σ é definido como:

$\ Rho_ {X, Y} = {\ mathrm {cov} (X, Y) \ over \ sigma_X \ sigma_Y} = {E ((X- \ mu_X) (Y \ mu_Y)) \ over \ sigma_X \ sigma_Y} ,$

onde E é a operador valor esperado e COV meios covariância. Desde μ _X = E (X), _X ² = σ E (X ²⁾ - E ² (X) e do mesmo modo para Y, que podem também escrever

$\ Rho_ {X, Y} = \ frac {E (XY) -E (X) E (Y)} {\ sqrt {E (X ^ 2) -E ^ 2 (X)} ~ \ sqrt {E (Y ^ 2) ^ 2 -E (Y)}}.$

A correlação é definido somente se ambos os desvios padrão são finitos e os dois são diferentes de zero. É um corolário da desigualdade de Cauchy-Schwarz que a correlação não pode exceder 1 em valor absoluto .

A correlação é 1 no caso de um aumento da relação linear, -1 no caso de uma relação linear decrescente, e algum valor no meio em todos os outros casos, que indica o grau de dependência linear entre as variáveis. Quanto mais próximo o coeficiente é de ou -1 ou 1, mais forte é a correlação entre as variáveis.

Se as variáveis são independente, então a correlação é 0, mas o inverso não é verdadeiro porque o coeficiente de correlação detecta apenas dependências lineares entre duas variáveis. Aqui está um exemplo: suponha que a variável aleatória X é uniformemente distribuída no intervalo de -1 a 1, e Y = X ^2. Em seguida, Y é completamente determinada por X, a fim de que X e Y são dependentes, mas a sua correlação é zero; eles são não correlacionadas. No entanto, no caso especial em que X e Y são conjuntamente normal, uncorrelatedness é equivalente a independência.

Uma correlação entre duas variáveis é diluído na presença de erros de medição em torno de estimativas de uma ou ambas as variáveis, caso em que disattenuation proporciona um coeficiente mais precisa.

Interpretação geométrica de correlação

O coeficiente de correlação, também pode ser visto como o co-seno do ângulo entre os dois vectores de amostras retiradas das duas variáveis aleatórias.

Atenção: Este método apenas funciona com dados centrado, isto é, os dados que foram modulados pela média da amostra de modo a ter uma média de zero. Alguns profissionais preferem um coeficiente de correlação uncentered (não-Pearson-compliant). Veja o exemplo abaixo para uma comparação.

Como exemplo, suponha que cinco países são encontrados para ter produtos nacionais brutos de 1, 2, 3, 5 e 8 bilhões de dólares, respectivamente. Suponhamos que estes mesmos cinco países (na mesma ordem) são encontrados a ter 11%, 12%, 13%, 15%, 18% e pobreza. Em seguida, deixou x e y ser encomendado vectores de 5 elementos que contêm os dados acima: x = (1, 2, 3, 5, 8) e y = (0.11, 0.12, 0.13, 0.15, 0.18).

Pelo procedimento habitual para encontrar o ângulo entre dois vetores (ver ponto produto), o coeficiente de correlação é descentrada:

$\ Cos \ theta = \ frac {\ bold {x} \ cdot \ bold {y}} {\ left \ | \ bold {x} \ right \ | \ left \ | \ bold {y} \ right \ | =} \ frac {2.93} {\ sqrt {103} \ sqrt {0,0983}} = 0,920814711.$

Note-se que os dados acima foram deliberadamente escolhido para ser perfeitamente correlacionados: y = 0,10 + 0,01 x. O coeficiente de correlação de Pearson deve, portanto, ser exatamente um. Centrar os dados (deslocando x por E (x) = 3,8 e y por E (y) = 0,138) os rendimentos x = (-2,8, -1,8, -0,8, 1,2, 4.2) e y = (-0,028, -0,018, -0,008, 0,012, 0,042), a partir dos quais

$\ Cos \ theta = \ frac {\ bold {x} \ cdot \ bold {y}} {\ left \ | \ bold {x} \ right \ | \ left \ | \ bold {y} \ right \ | =} \ frac {0,308} {\ sqrt {30,8} \ sqrt {0,00308}} = 1 = \ rho_ {xy},$

como esperado.

A motivação para a forma do coeficiente de correlação

Outra motivação para a correlação vem de inspecionar o método de simples regressão linear . Tal como acima, X é o vector de variáveis independentes, 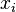$x_i$ E Y das variáveis dependentes, 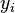$y_i$ E uma relação linear simples entre X e Y é procurado, através de um método de mínimos quadrados na estimativa de Y:

$\ Y = X \ beta + \ varepsilon. \,$

Em seguida, a equação da linha de mínimos quadrados pode ser derivada para ser da forma:

$(Y - \ bar {Y}) = \ frac {n \ soma x_iy_i- \ sum x_i \ sum y_i} {n \ sum x_i ^ 2 - (\ sum x_i) ^ 2} (X - \ bar {X})$

que pode ser reorganizada na forma:

$(Y - \ bar {Y}) = \ frac {r s_y} {} s_x (X- \ bar {X})$

em que r tem a forma familiar mencionado acima: 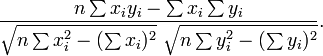$\ Frac {n \ sum x_iy_i- \ sum x_i \ sum y_i} {\ sqrt {n \ sum x_i ^ 2 - (\ sum x_i) ^ 2} ~ \ sqrt {n \ soma y_i ^ 2 - (\ y_i soma) ^ 2}}.$

Interpretação do tamanho de uma correlação

Correlação	Negativo	Positivo
Pequeno	-0.3 Para -0.1	0,1 a 0,3
Médio	-0.5 Para -0.3	0,3 a 0,5
Grande	-1.0 A -0.5	0,5 a 1,0

Vários autores têm oferecido diretrizes para a interpretação de um coeficiente de correlação. Cohen (1988), por exemplo, sugeriu as seguintes interpretações para correlações em pesquisa psicológica, na tabela à direita.

Como o próprio Cohen observou, no entanto, todos estes critérios são, de certa forma arbitrária e não deve ser observado muito estritamente. Isto é porque a interpretação de um coeficiente de correlação depende do contexto e objectivos. A correlação de 0,9 pode ser muito baixa se está a verificar uma lei física por meio de instrumentos de alta qualidade, mas pode ser considerada muito elevada nas ciências sociais em que pode haver uma maior contribuição dos fatores complicadores.

Ao longo desta veia, é importante lembrar que "grandes" e "pequenos" não devem ser tomadas como sinônimos de "bom" e "ruim" em termos de determinar que uma correlação é de um determinado tamanho. Por exemplo, uma correlação de 1,0 ou -1,0 indica que as duas variáveis são analisadas módulo de escalonamento equivalente. Cientificamente, este com mais freqüência indica um resultado trivial do que uma terra tremer um. Por exemplo, considere a descoberta de uma correlação de 1,0 entre quantos pés de altura um grupo de pessoas são eo número de polegadas da parte inferior de seus pés para o alto de suas cabeças.

Coeficientes de correlação não paramétricos

Coeficiente de correlação de Pearson é uma estatística paramétrica e quando as distribuições não são normais, pode ser menos útil do que métodos de correlação não paramétricos, tais como Qui-quadrado, Aponte correlação biserial, Ρ de Spearman e Τ de Kendall. Eles são um pouco menos potente do que os métodos paramétricos se são cumpridos os pressupostos subjacentes ao último, mas são menos propensos a dar resultados distorcidos quando os pressupostos falham.

Outras medidas de dependência entre variáveis aleatórias

Para obter uma medida para mais dependências gerais nos dados (também não-linear), é melhor usar o coeficiente de correlação, que é capaz de detectar quase qualquer dependência funcional, ou a baseada entropia- informação mútua / correlação total que é capaz de detectar mesmo as dependências mais gerais. Estes últimos são por vezes referido como medidas de correlação multi-momento, em comparação com aqueles que consideram apenas segundo momento (em pares ou quadrática) dependência.

O correlação policóricas é outra correlação aplicada a dados ordinal que tem como objetivo estimar a correlação entre variáveis latentes teorizadas.

Cópulas e correlação

A informação dada por um coeficiente de correlação não é suficiente para definir a estrutura de dependência entre variáveis aleatórias; capturá-lo totalmente, devemos considerar uma cópula entre eles. O coeficiente de correlação define completamente a estrutura de dependência apenas em casos muito especiais, por exemplo quando o funções de distribuição cumulativas são o distribuições normais multivariadas. No caso de distribuições elípticas que caracteriza os (hiper) elipses de igual densidade, no entanto, não caracteriza completamente a estrutura de dependência (por exemplo, o grau de distribuição t uma multivariada de liberdade determinar o nível de dependência caudal).

Matrizes de correlação

A matriz de correlação de variáveis aleatórias X n _1, ..., X _n é o n × cuja matriz n i, j é corr entrada (X _i, X _j). Se as medidas de correlação são usados coeficientes de produto-momento, a matriz de correlação é a mesma que a matriz de covariância das variáveis aleatórias padronizados X _i / SD _(i X) para i = 1, ..., n. Por conseguinte, é necessariamente uma matriz positiva-semidefinite.

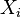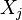A matriz de correlação é simétrica, pois a correlação entre $X_i$ e $X_j$ é o mesmo que a correlação entre 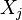$X_j$ e $X_i$ .

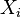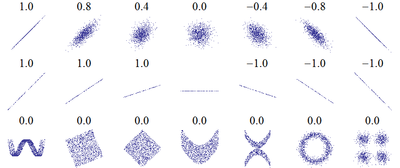
Correlação Remoção

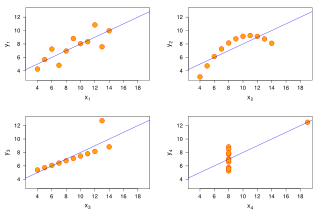
É sempre possível retirar a correlação entre as variáveis aleatórias de zero-média com um linear transformar, mesmo se a relação entre as variáveis não é linear. Suponha que um vetor de variáveis aleatórias n é amostrado m vezes. Seja X uma matriz onde 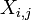$X_ {i, j}$ é variável j th de amostra i. Deixar 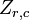$Z_ {r, c}$ ser um r por c matriz com cada elemento 1. Então D é os dados transformados assim que cada variável aleatória tem média zero, e T é os dados transformados de modo todas as variáveis têm média zero, variância unitária, e correlação nula com todas as outras variáveis. As variáveis não correlacionadas serão transformadas, mesmo que eles não podem ser independente.

$D = X - \ frac {1} {m} Z_ {m, m} X$

$T = D (D ^ T D) ^ {- \ frac {1} {2}}$

onde um expoente da -1/2 representa o raiz quadrada da matriz inversa de uma matriz. A matriz de covariância de T será a matriz identidade. Se uma nova amostra de dados x é um vector da linha de n elementos, em seguida, a mesma transformação pode ser aplicada a X para obter os vectores transformados d e t:

$d = x - \ frac {1} {m} Z_ {1, m} X$

$t = d (D ^ T D) ^ {- \ frac {1} {2}}.$

Equívocos comuns sobre correlação

Correlação e causalidade

O dito convencional de que " a correlação não implica causalidade "significa que a correlação não pode ser validamente usado para inferir uma relação causal entre as variáveis. Esta máxima não deve ser entendida no sentido de que as correlações não pode indicar relações causais. No entanto, as causas subjacentes a correlação, se houver, pode ser indirecta e desconhecido. Por conseguinte, o estabelecimento de uma correlação entre duas variáveis não é uma condição suficiente para estabelecer uma relação causal (em qualquer direção).

Aqui está um exemplo simples: tempo quente pode causar tanto o crime e gelados compras. Portanto crime está relacionada com compras de gelados. Mas o crime não causar compras de gelados e as compras de gelados não causam crime.

A correlação entre idade e altura em crianças é bastante causalmente transparente, mas uma correlação entre o humor e saúde nas pessoas é menos. Será melhora do humor liderança para a melhoria da saúde? Ou faz boa vantagem de saúde para bom humor? Ou será que algum outro fator subjacente a ambos? Ou é pura coincidência? Em outras palavras, esta correlação pode ser tomada como evidência de uma possível relação causal, mas não pode indicar que a relação causal, se houver, pode ser.

Correlação e linearidade

Quatro conjuntos de dados com a mesma correlação de 0,81

Embora a correlação de Pearson indica a força de uma relação linear entre duas variáveis, o seu valor por si só pode não ser suficiente para avaliar essa relação, especialmente no caso em que o pressuposto de normalidade é incorrecta.

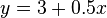A imagem à direita mostra scatterplots de Quarteto de Anscombe, um conjunto de quatro diferentes pares de variáveis criadas por Francis Anscombe. Os quatro $y$ variáveis têm a mesma média (7.5), o desvio padrão (4,12), a correlação (0,81) e da linha de regressão ( $y = 3 + 0.5x$ ). No entanto, como pode ser visto nas parcelas, a distribuição das variáveis é muito diferente. A primeira (superior esquerdo) parece ser distribuído normalmente, e corresponde ao que seria de esperar quando se considera duas variáveis correlacionadas e seguindo a suposição de normalidade. O segundo (canto superior direito) não é distribuído normalmente; enquanto que uma relação evidente entre as duas variáveis pode ser observado, não é linear, e o coeficiente de correlação de Pearson não é relevante. No terceiro caso (canto inferior esquerdo), a relação linear é perfeito, exceto por uma outlier que exerce influência suficiente para diminuir o coeficiente de correlação 1-0,81. Finalmente, o quarto exemplo (inferior direito) mostra um outro exemplo, quando um outlier é suficiente para produzir um coeficiente de correlação elevado, mesmo que a relação entre as duas variáveis não é linear.

Estes exemplos indicam que o coeficiente de correlação, tal como um resumo estatístico, não pode substituir o exame individual dos dados.

Calculando correlação com precisão numa única passagem

O algoritmo seguinte (em pseudocódigo) irá calcular Correlação de Pearson com boa estabilidade numérica.

 sum_sq_x = 0 sum_sq_y = 0 = 0 sum_coproduct mean_x = x [1] mean_y = y [1] para i em 2 a N: varredura = (i - 1.0) / i delta_x = x [i] - mean_x delta_y = y [i ] - mean_y sum_sq_x + = delta_x * * delta_x varredura sum_sq_y + = delta_y * * delta_y varredura sum_coproduct + = delta_x * * delta_y varredura mean_x + = delta_x / i mean_y + = delta_y / i pop_sd_x = sqrt (sum_sq_x / N) pop_sd_y = sqrt (sum_sq_y / N) cov_x_y = sum_coproduct / N correlação = cov_x_y / (pop_sd_x * pop_sd_y)

Retirado de " http://en.wikipedia.org/w/index.php?title=Correlation_and_dependence&oldid=199055311 "