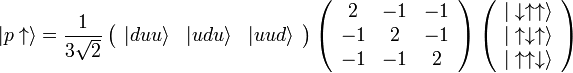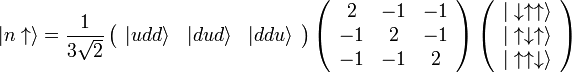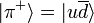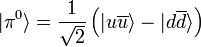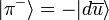Isospin
Fundo para as escolas Wikipédia
SOS acredita que a educação dá uma chance melhor na vida de crianças no mundo em desenvolvimento também. Antes de decidir sobre o patrocínio de uma criança, por que não aprender sobre as diferentes instituições de caridade de patrocínio primeiro ?
| Sabor em física de partículas |
Flavour números quânticos:
Números quânticos relacionados:
Combinações:
|
Em física , e, especificamente, a física de partículas , isospin (spin isotópico, rotação isobaric) é uma número quântico relacionados com a interação forte. Este termo foi derivado de rotação isotópica, mas a rotação isotópica termo é confuso como dois isótopos de um núcleo ter diferentes números de núcleos; Em contraste, as rotações de isospin manter o número de núcleos. Os físicos nucleares preferem rotação isobaric, que é mais preciso em significado. Isospin simetria é um subconjunto do sabor simetria visto de forma mais ampla nas interações de bárions e mésons. Simetria de isospin permanece um conceito importante em física de partículas, e um exame atento desta simetria historicamente levou diretamente para a descoberta e compreensão de quarks e do desenvolvimento de Teoria de Yang-Mills.
Motivação para isospin
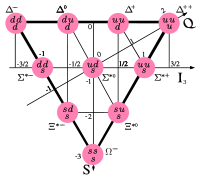

Isospin foi introduzido por Werner Heisenberg em 1932 (apesar de ter sido nomeado por Eugene Wigner em 1937) para explicar simetrias do então recém-descoberto de nêutrons :
- A massa do neutrão e do protão são quase idênticos: eles são quase degenerada, e ambos são assim frequentemente chamada nucleons. Embora o próton tem uma carga positiva, e a neutrões é neutro, que são quase idênticas em todos os outros aspectos.
- A força da forte interacção entre qualquer par de núcleos é a mesma, independentemente de como eles estão interagindo protões ou neutrões como.
Assim, isospin foi introduzido como um conceito bem antes do desenvolvimento na década de 1960 do modelo de quark que fornece a nossa compreensão moderna.
O nucleons, bárions de spin 1/2, foram agrupados juntos porque ambos têm quase a mesma massa e interagir em quase da mesma maneira. Assim, foi conveniente para tratá-los como sendo diferentes estados de uma mesma partícula. Desde um spin 1/2 partícula tem dois estados, os dois estavam a ser dito de isospin 1/2. O próton e do nêutron foram associados com diferentes projeções isospin I z = + 1/2 e - 1/2, respectivamente. Ao construir uma teoria física de forças nucleares, pode-se então simplesmente assumir que ele não depende de isospin.
Estas considerações também revelar-se útil na análise de interacções mesões-nucleônicas após a descoberta da pions em 1947. Os três pions (π +, π 0, π -) poderia ser atribuído a um tripleto com isospin I = 1 e I z = 1, 0 ou -1. Ao assumir que isospin foi conservado por interações nucleares, os novos mesões foram mais facilmente acomodado pela teoria nuclear.
Como outras partículas foram descobertos, que eles foram divididos em multipletos isospin de acordo com o número de diferentes estados de carga visto: um dupleto I = 1/2 de K mesões, um tripleto I = 1 de bariones Σ, um único I = 0 Λ, quatro I = 3/2 Δ bariones, e assim por diante. Esta estrutura foi combinada com multipleto estranheza Murray Gell-Mann Eightfold Way, em última instância, para o modelo de quark e cromodinâmica quântica.
Compreensão moderna da isospin
Observação da luz bariones (aqueles feitos de acima, para baixo e quarks estranhos) nos levam a crer que algumas destas partículas são tão semelhantes em termos da sua interacções fortes que podem ser tratados como diferentes estados da mesma partícula. No entendimento moderno de cromodinâmica quântica, é porque cima e para baixo quarks são muito semelhantes em massa, e têm as mesmas interações fortes. Partículas feitas dos mesmos números de cima e para baixo quark têm massas semelhantes e são agrupados em conjunto. Por exemplos, as partículas conhecido como o Bárions Delta - bárions de rotação 3/2 feita de uma mistura de três quarks up e down - são agrupados juntos, porque todos eles têm quase a mesma massa (aproximadamente 1232 MeV / C 2), e interagir em quase da mesma maneira.
No entanto, porque os quark cima e para baixo têm diferentes taxas de (2/3-E e - 1/3-E, respectivamente), os quatro deltas também têm diferentes taxas (Δ ++ (uuu), Δ + (uud), Δ 0 (UDD ), Δ - (DDD)). Estes deltas poderiam ser tratados como o mesmo partícula e a diferença de carga sendo devido à partícula estar em diferentes estados. Isospin foi concebida como um paralelo a girar para associar uma projeção isospin (denotada I z ou I 3) para cada estado carregado. Desde há quatro Deltas, foram necessários quatro projeções. Porque isospin foi modelado em rotação, as projeções isospin foram feitas para variar em incrementos de 1 e de ter quatro incrementos de 1, você precisava de um valor de isospin de 3/2 (dando a projeções I z = 3/2, 1/2, - 1/2, -. 3/2 Assim, todos os deltas foram dito ter isospin I = 3/2 e cada carga diferente indivíduo teve I Z (por exemplo, o Δ ++ foi associada com I z = + 3/2) .
Depois que o modelo quark foi elaborado, notou-se que a projeção isospin estava relacionada com a cima e para baixo teor de partículas quark. A relação é que eu z = 1/2 (N u - N d) onde N u d e N são o número de quarks up e down, respectivamente.
Na foto isospin, os quatro Deltas e os dois núcleos foram pensados para ser os diferentes estados de duas partículas. No modelo de quark, os Deltas pode ser pensado como os estados excitados dos núcleos.
Simetria de isospin
Na mecânica quântica , quando um Hamiltonian tem uma simetria, simetria que se manifesta através de um conjunto de estados que têm a mesma energia; isto é, os estados são degenerada. Em física de partículas , o próximo mass-degenerescência dos pontos de nêutrons e prótons a uma simetria aproximada do Hamiltoniano descrever as interações fortes. O nêutron tem uma massa ligeiramente superior devido à quebra isospin; isto é devido à diferença nas massas de cima e para baixo quark e os efeitos da interacção electromagnética. No entanto, o aparecimento de uma simetria aproximada é ainda útil, uma vez que as pequenas quebras pode ser descrito por uma teoria de perturbação, o que dá origem a pequenas diferenças entre os estados quase degenerados.
SU (2)
Contribuição de Heisenberg foi notar que a formulação matemática desta simetria foi, em alguns aspectos semelhante à formulação matemática rotação, daí o nome "isospin" deriva. Para ser mais preciso, a simetria de isospin é dada pela invariância da Hamiltoniana das interacções fortes sob a acção do Grupo de Lie SU (2). O neutrões e o protão são atribuídos ao dupleto (o spin 1/2, 2, ou representação fundamental) de SU (2). Os piões são atribuídos ao tripleto (spin-1, 3, ou representação adjunta) de SU (2).
Tal como é o caso para a rotação regular, isospin é descrita por dois números quânticos, eu, o isospin total, e eu z, o componente do vector de rotação em alguma direção.
Relação com sabor
A descoberta e subsequente análise de partículas adicionais, tanto mésons e bárions, deixou claro que o conceito de simetria de isospin poderia ser ampliado para um grupo de simetria ainda maior, chamado agora simetria sabor. Uma vez o kaons e sua propriedade de estranheza se tornou melhor compreendida, começou a ficar claro que estes, também, parecia ser uma parte de uma simetria alargada que continha isospin como um subgrupo. A simetria foi nomeado o maior Maneira de oito vezes por Murray Gell-Mann, e foi prontamente reconhecida para corresponder à representação adjunta de SU (3). Para entender melhor a origem desta simetria, Gell-Mann propôs a existência de cima, para baixo e estranhas quarks que pertencem à representação fundamental do SU (3) simetria sabor.
Embora simetria isospin é muito ligeiramente quebrado, SU (3) simetria é mais mal quebrado, devido ao muito maior massa do quark estranho em comparação com o de cima a baixo. A descoberta de encanto, bottomness e topness poderia levar a novas expansões até SU (6) simetria sabor, mas as grandes massas desses quarks faz essas simetrias quase inútil. Em aplicações modernas, como grade QCD, simetria isospin é muitas vezes tratada como exata enquanto os quarks mais pesados devem ser tratados separadamente.
Conteúdo Quark e isospin
Quarks up e down têm cada isospin I = 1/2, e isospin z-componentes (I z) de 1/2 e - 1/2, respectivamente. Todos os outros têm quark I = 0. Um compósito feito de partículas de quark deve ter eu z igual à soma de I z dos seus quark e inferior ou igual
- Partículas de iso-spin 3/2 só pode ser feita por uma mistura de três u e d quark (Δ de).
- Partículas de isospin 1 são feitos de uma mistura de dois quark u e d quark (Σ de π, 's, ρ' s, etc).
- Partículas de iso-spin 1/2 pode ser feito de uma mistura de três u e d quark (N 's) ou a partir de um u ou d quark (Ξ de, K' s, 's, D, etc.)
- Partículas de isospin 0 pode ser feito de um U e uma d quark (Λ de, η 's, ω' s, etc), ou a partir de qualquer u ou d quark em todos os (de Ω, φ 's, etc).
| Grupo baryon | EU | I z = + 3/2 | I z = 1 | I z = + 1/2 | I z = 0 | I Z = - 1/2 | I z = -1 | I Z = - 3/2 |
|---|---|---|---|---|---|---|---|---|
| Deltas | 3/2 | Δ ++ (uuu) | Δ + (uud) | Δ 0 (UDD) | Δ - (ddd) | |||
| Sigmas | 1 | Σ + (uus) | Σ 0 (uds) | Σ - (DDS) | ||||
| Charmed Sigmas | 1 | Σ ++ c (UUC) | Σ + c (UDC) | Σ 0 c (DDC) | ||||
| Inferior Sigmas | 1 | Σ + b (Uub) | Σ 0 b (UDB) | Σ - b (DDB) | ||||
| Nucleons | 1/2 | p + (uud) | n 0 (UDD) | |||||
| Xis | 1/2 | Ξ 0 (USS) | Ξ - (DSS) | |||||
| Charmed Xis | 1/2 | Ξ + c (USC) | Ξ 0 c (DSC) | |||||
| Duplo Xis encantada | 1/2 | Ξ ++ cc (UCC) | Ξ + cc (DCC) | |||||
| Inferior Xis | 1/2 | Ξ 0 b (USB) | Ξ - b (DSB) | |||||
| Xis inferior Charmed | 1/2 | Ξ + cb (UCB) | Ξ 0 cb (DCB) | |||||
| Duplo Xis fundo | 1/2 | Ξ 0 bb (UBB) | Ξ - bb (DBB) | |||||
| Lambdas | 0 | Λ 0 (uds) | ||||||
| Charmed Lambdas | 0 | Λ + c (UDC) | ||||||
| Inferior Lambdas | 0 | Λ 0 b (UDB) | ||||||
| Omegas | 0 | Ω - (sss) | ||||||
| Charmed Omegas | 0 | Ω 0 c (SSC) | ||||||
| Duplo Omegas encantada | 0 | Ω + cc (SCC) | ||||||
| Omegas de fundo | 0 | Ω - b (SSB) | ||||||
| Omegas inferior Charmed | 0 | Ω 0 cb (SCB) | ||||||
| Duplo Omegas fundo | 0 | Ω - bb (SBB) | ||||||
| Triplo Charmed Omegas | 0 | Ω ++ ccc (ccc} | ||||||
| Duplo Omegas inferior encantada | 0 | Ω + CCB (CCB) | ||||||
| Charmed Omegas duplo fundo | 0 | Ω 0 CBB (CBB) | ||||||
| Omegas triple bottom | 0 | Ω - bbb (bbb) |
Simetria de isospin de quarks
No âmbito do Modelo Padrão , a simetria isospin do próton e do nêutron são reinterpretados como a simetria do isospin -se e quarks para baixo. Tecnicamente, os estados nucleon gibão são vistos como combinações lineares de produtos de 3 partículas estados isospin gibão e estados de spin gibão. Isto é, o (spin-up) de protões função de onda, em termos de auto-estados quark-sabor, é descrito por
eo (spin-up) de nêutrons por
Aqui, 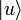 é o quark up sabor eigenstate, e
é o quark up sabor eigenstate, e 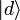 é o para baixo quark sabor eigenstate, enquanto
é o para baixo quark sabor eigenstate, enquanto 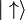 e
e 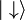 são os auto-estados de
são os auto-estados de 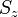 . Embora essas superposições são a maneira tecnicamente correta de denotar um próton e do nêutron em termos de sabor quark e de spin eigenstates, por brevidade, eles são muitas vezes referida como uud e udd. Note também que a derivação acima é exata assume simetria isospin e é modificado por termos SU (2) -breaking.
. Embora essas superposições são a maneira tecnicamente correta de denotar um próton e do nêutron em termos de sabor quark e de spin eigenstates, por brevidade, eles são muitas vezes referida como uud e udd. Note também que a derivação acima é exata assume simetria isospin e é modificado por termos SU (2) -breaking.
Do mesmo modo, a simetria isopsin dos piões são dadas por:
Isospin fraco
Isospin é semelhante, mas não deve ser confundido com isospin fraco. Resumidamente, isospin fraco é o calibre da simetria interação fraca que liga quarks e léptons dupletos de partículas canhotos em todas as gerações; por exemplo, para cima e para baixo quarks, top e bottom quarks, elétrons e neutrinos do elétron. Isospin conecta-se somente quarks up e down, atua em ambos quiralidades (esquerda e direita) e é uma (não um medidor) simetria global.
Simetria isospin aferido
Têm sido feitas tentativas para promover a partir de um isospin global para uma simetria local. Em 1954, Chen Ning Yang e Robert Mills sugeriu que a noção de prótons e nêutrons, que são continuamente giradas em si por isospin, devem ser autorizados a variar de ponto a ponto. Para descrever isso, a direção de prótons e nêutrons no espaço isospin deve ser definido em cada ponto, dando base local para isospin. A conexão calibre, então, descrever como transformar isospin ao longo de um caminho entre dois pontos.
Este Teoria de Yang-Mills descreve interagindo bósons vetores, como o fóton do eletromagnetismo. Ao contrário do fóton, o SU (2) teoria de calibre conteria bósons auto-interagindo. A condição de medidor de invariância sugere que eles têm massa zero, tal como no eletromagnetismo.
Ignorar o problema sem massa, como Yang e Mills fez, a teoria faz uma previsão firme: a partícula vector deveria casal para todas as partículas de um determinado isospin universalmente. O acoplamento para o nucleão seria o mesmo que o acoplamento à kaons. O acoplamento para o piões seria o mesmo que o auto-acoplamento dos bosões vector a si próprios.
Quando Yang e Mills propôs a teoria, não houve Higgs candidato vector. JJ Sakurai em 1960 previu que não deve haver uma enorme Higgs vector que está acoplado a isospin, e previu que mostram acoplamentos universais. O mésons Rho foram descobertos pouco tempo depois, e foram rapidamente identificados como bósons vetores de Sakurai. Os acoplamentos da rho aos núcleos e uns aos outros foram verificados para ser universal, da melhor forma experimento poderia medir. O facto de a corrente de isospin diagonal contém parte da corrente electromagnética levou à previsão de mistura Rho-fotão e o conceito de dominância méson vetor, idéias que levaram às imagens teóricos bem sucedidos de GeV escala fóton-núcleo de espalhamento.
Embora a descoberta dos quarks levou a reinterpretação do méson rho como um vetor vinculado estado de um quark e um antiquark, às vezes é ainda útil para pensar sobre isso como o bóson de calibre de uma simetria local escondido