Computador quântico

Assuntos Relacionados: hardware e infra-estrutura de computação

Você sabia ...

SOS acredita que a educação dá uma chance melhor na vida de crianças no mundo em desenvolvimento também. Patrocinar uma criança para fazer uma diferença real.

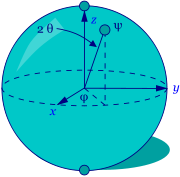
O Esfera Bloch é uma representação de um qubit, o alicerce fundamental dos computadores quânticos.

Um computador quântico é um dispositivo para computação que faz uso direto de distintamente mecânica quântica fenômenos, tais como superposição e entrelaçamento, a executar operações em dados. Em um computador clássica (ou convencional), a informação é armazenada como bits; em um computador quântico, que é armazenado como qubits (qu antum bi ts digi nary). O princípio básico de computação quântica é que as propriedades quânticas pode ser usada para representar e estrutura de dados, e que os mecanismos quânticos pode ser concebido e construído para executar operações com estes dados.

Embora a computação quântica ainda está em sua infância, experimentos foram realizados em que as operações computacionais quânticos foram executados em um número muito pequeno de qubits. Tanto a pesquisa prática e teórica continua com interesse, e muitas agências governamentais de financiamento nacional e militar apoiar a investigação computação quântica para desenvolver computadores quânticos, tanto para fins de segurança civis e nacionais, tais como criptoanálise.

Se computadores quânticos em larga escala pode ser construído, eles serão capazes de resolver certos problemas muito mais rápido do que qualquer um de nossos computadores clássicos atuais (por exemplo Algoritmo de Shor). Os computadores quânticos são diferentes de outros computadores , tais como Computadores de DNA e os computadores tradicionais com base em transistores. Algumas arquiteturas de computação, tais como computadores ópticos podem utilizar superposição clássica de ondas eletromagnéticas. Sem alguns recursos mecânicos especificamente quânticos tais como emaranhamento, conjectura-se que uma vantagem exponencial sobre os computadores clássicos não é possível.

Base

Um computador clássico tem uma memória composta de bits, em que cada bit possua ou um um ou um zero. Um computador quântico mantém uma seqüência de qubits. Um único qubit pode conter um, um zero, ou, fundamentalmente, um superposição quântica destes; além disso, um par de qubits podem estar em uma superposição quântica de 4 estados e três qubits em uma superposição de 8. Em geral, um computador quântico com n qubits pode ser em até 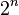$2 ^ n$ diferentes estados simultaneamente (isso se compara a um computador normal que só pode estar em um destes 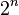$2 ^ n$ afirma a qualquer momento). Um computador quântico funciona através da manipulação desses qubits com uma sequência fixa de portas lógicas quânticas. A seqüência de portas a serem aplicadas é chamado de um algoritmo quântico.

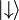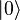Um exemplo de uma implementação de qubits para um computador quântico poderia começar com o uso de partículas com dois girar estados: "up" e "down" (tipicamente escrito $| {\ Uparrow} \ rangle$ e $| {\ Downarrow} \ rangle$ Ou $| 0 \ rangle$ e $| 1 \ rangle$ ). Mas, na realidade, qualquer sistema que possui um Uma quantidade observável que é conservada sob evolução temporal e tais que A tem, pelo menos, dois períodos consecutivos e suficientemente discretos espaçados valores próprios , é um candidato adequado para a implementação de um qubit. Isso é verdade porque tal sistema pode ser mapeado sobre um eficaz girar-1/2 sistema.

Bits vs. Qubits

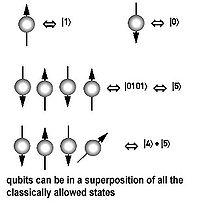
Qubits são compostos de partículas controlados e os meios de controlo (por exemplo, dispositivos que capturar partículas e eles mudam de um estado para outro).

Considere-se primeiro um computador clássico, que opera em um três-bit registe-se. O estado do computador em qualquer momento é uma distribuição de probabilidade sobre o $2 ^ 3 = 8$ diferentes cadeias de três bit 000, 001, ..., 111-assim está descrita por oito números não negativos (a, b, c, d, e, f, g, h) -adding-se a um.

O estado de um computador quântico de três qbit é igualmente descrita por um vector de oito-dimensional (a, b, c, d, e, f, g, h), uma chamada wavefunction. No entanto, em vez de adicionar a um, a soma dos quadrados das magnitudes de coeficiente, 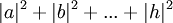$| A | ^ 2 + | b | ^ 2 + ... + | h | ^ 2$ , Deve ser igual a um. Além disso, os coeficientes são números complexos que precisam não ser não-negativo. O fato de que os coeficientes pode ser negativo, bem como positivo permite a anulação, ou interferência, entre os diferentes caminhos computacionais, e é uma diferença fundamental entre a computação quântica e computação clássica probabilística.

Se você medir os três qubits, então você vai observar uma seqüência de três bits. A probabilidade de medir uma seqüência será igual ao quadrado magnitude dos coeficientes dessa cadeia. Assim, uma medição do estado quântico com coeficientes (a, b, ..., h) mostra a distribuição de probabilidade clássica 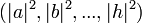$(| A | ^ 2, | b | ^ 2, ..., | h | ^ 2)$ . Nós dizemos que o estado quântico "desmorona" a um estado clássico.

Note-se que um vector de oito-dimensional podem ser especificados de muitas maneiras diferentes, dependendo do que base que você escolher para o espaço. A base de cordas de três bit 000, 001, ..., 111 é conhecida como a base computacional, e é muitas vezes conveniente, mas outras bases de unidade de comprimento, vectores ortogonais também pode ser usado. Notação Ket é frequentemente usada para tornar explícita a escolha da base. Por exemplo, o estado (a, b, c, d, e, f, g, h) na base computacional pode ser escrito como 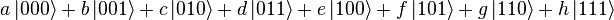$a \, | 000 \ rangle + b \, | 001 \ rangle + c \, | 010 \ rangle + d \, | 011 \ rangle + e \, | 100 \ rangle + f \, | 101 \ rangle + g \ , | 110 \ rangle + h \, | 111 \ rangle$ , Onde, por exemplo, 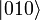$| 010 \ rangle$ = (0,0,1,0,0,0,0,0). 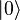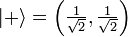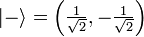A base computacional para um único qubit (duas dimensões) é $| 0 \ rangle$ = (1,0), $| 1 \ rangle$ = (0,1), mas uma outra base comum é a base de Hadamard $| + \ Rangle = \ left (\ tfrac {1} {\ sqrt {2}}, \ tfrac {1} {\ sqrt {2}} \ right)$ e $| - \ Rangle = \ left (\ tfrac {1} {\ sqrt {2}}, - \ tfrac {1} {\ sqrt {2}} \ right)$ .

Observe que, embora a gravação de um estado clássico de n bits, uma distribuição de probabilidade ^{n-dimensional} 2, requer um número exponencial de números reais, praticamente podemos sempre pensar no sistema como sendo exatamente um dos n bit seqüências de nós apenas don ' t sabe qual. Quanticamente, isso não é mais o caso, e todos os 2 coeficientes ⁿ complexos precisam ser mantidos a par de para ver como o sistema quântico evolui. Por exemplo, um computador quântico de 300 qubits tem um estado descrito por 2 ³⁰⁰ (cerca de 10) ⁹⁰ números complexos, mais do que o número de átomos no universo observável .

Operação

Enquanto um estado de três bits clássica e um estado de três qubit quântica são ambos de oito dimensional vetores, eles são manipulados de forma bastante diferente para a computação clássica ou quântica, respectivamente. Para a computação em qualquer dos casos, o sistema tem de ser inicializado, por exemplo, na cadeia de tudo zeros, ou seja, (1,0,0,0,0,0,0,0) ou 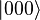$| 000 \ rangle$ . Em computação randomizado clássica, o sistema evolui de acordo com a aplicação de matrizes estocásticas, que preservam a que as probabilidades de adicionar-se a um (isto é, a preservar L1 norma). Em computação quântica, por outro lado, são permitidas as operações matrizes unitárias, que são efetivamente rotações (eles preservam que a soma dos quadrados somam um, o Euclidiana ou norma L2). (Exatamente o que unitaries pode ser aplicada dependerá a física do dispositivo quântica.) Consequentemente, uma vez que as rotações pode ser desfeita girando para trás, cálculos quânticos são reversível. (Tecnicamente, as operações quânticas podem ser combinações probabilísticas de unitaries, de modo a computação quântica realmente generalizar computação clássica. Veja circuito quântico para uma formulação mais precisa.)

Finalmente, após a rescisão do algoritmo, o resultado deve ser lido. No caso de um computador clássico, que amostra a partir da distribuição de probabilidade no registo de três bits para obter uma determinada corda de três bits, digamos 000 quanticamente, nós medir o estado de três qbit, que é equivalente ao colapso do estado quântico para baixo para uma distribuição clássica (com os coeficientes no estado clássico sendo as magnitudes quadrados dos coeficientes para o estado quântico, tal como descrito acima) seguido por amostragem a partir dessa distribuição . Note que isto destrói o estado quântico originais. Muitos algoritmos só vai dar a resposta correta com uma certa probabilidade, porém por inicializar repetidamente, execução e medição do computador quântico, a probabilidade de obter a resposta correta pode ser aumentado. Por exemplo, executar o algoritmo de Shor factorisation quatro vezes dará a resposta correta com uma probabilidade muito elevada.

Para mais detalhes sobre as sequências de operações utilizados para vários algoritmos, veja computador quântico universal, Algoritmo de Shor, Algoritmo de Grover, Algoritmo de Deutsch-Jozsa, transformação de Fourier quântica, porta quântica, algoritmo quântico e adiabatic correção de erro quântico.

Potencial

Fatoração inteiro é acreditado para ser computacionalmente inviável com um computador comum para grandes números inteiros que são o produto de apenas alguns números primos (por exemplo, produtos de dois números primos 300 algarismos). Em comparação, um computador quântico poderia resolver este problema de forma eficiente usando Algoritmo de Shor encontrar seus fatores. Esta capacidade permitiria que um computador quântico para "quebrar" muitos dos criptográficas sistemas em uso hoje em dia, no sentido de que haveria uma tempo polinomial (em número de bits do número inteiro) algoritmo para resolver o problema. Em particular, a maioria dos populares cifras chaves públicas são baseados na dificuldade de inteiros factoring (ou a conexo problema logaritmo discreto que também pode ser resolvido pelo algoritmo de Shor), incluindo formas de RSA. Estes são utilizados para proteger páginas seguras da Web, e-mail criptografado, e muitos outros tipos de dados. Quebrando estes teriam implicações significativas para a privacidade e segurança eletrônica. A única maneira de aumentar a segurança de um algoritmo como RSA seria aumentar o tamanho da chave e esperar que o adversário não tem os recursos para construir e usar um computador quântico poderoso o suficiente.

Uma forma de sair deste dilema seria a utilização de algum tipo de criptografia quântica. Há também alguns são esquemas de assinatura digital que são acreditados para ser seguro contra computadores quânticos. Ver, por exemplo Assinaturas de Lamport.

Esta dramática vantagem dos computadores quânticos só foi descoberto por fatoração e discretos logaritmos até agora. No entanto, não há nenhuma prova de que a vantagem é real: um algoritmo classical ingualmente rápido pode ainda ser descoberto. Há um outro problema em que os computadores quânticos têm um, embora significativo (quadrática) vantagem menor. É de busca de banco de dados de quantum, e pode ser resolvido pela Algoritmo de Grover. Neste caso, a vantagem é demonstrável. Isto estabelece além da dúvida que os computadores quânticos (ideais) são superiores aos computadores clássicos para pelo menos um problema.

Considere um problema que tem estas quatro propriedades:

A única maneira de resolver isso é adivinhar respostas repetidamente e verificá-las,
Existem n respostas possíveis para verificar,
Cada resposta possível leva a mesma quantidade de tempo para verificar, e
Não há pistas sobre quais respostas poderia ser melhor: gerar possibilidades aleatoriamente é tão bom como verificá-los em alguma ordem especial.

Um exemplo disto é um cracker de senhas que tenta adivinhar a senha para uma arquivo criptografado (assumindo que a senha tem um comprimento máximo possível).

Para problemas com todas as quatro propriedades, o tempo para um computador quântico para resolver este será proporcional à raiz quadrada de n (que levaria uma média de (n + 1) / 2 palpites para encontrar a resposta usando um computador clássico.) Isso pode ser um grande aumento de velocidade, reduzindo alguns problemas de anos para segundos. Ele pode ser usado para atacar cifras simétricas, tais como Triple DES e AES por tentativa de adivinhar a chave secreta. Independentemente de saber se qualquer um desses problemas pode ser mostrado para ter uma vantagem em um computador quântico, no entanto, eles sempre terão a vantagem de ser uma excelente ferramenta para o estudo de interações quânticas, o que por si só é um enorme valor para a comunidade científica.

Algoritmo de Grover também pode ser usado para se obter uma velocidade quadrática-up [através de uma pesquisa de força bruta] para uma classe de problemas conhecido como NP-completos.

Problemas

Há uma série de dificuldades práticas para a construção de um computador quântico, e, até agora, os computadores quânticos têm apenas resolveu problemas triviais. David DiVincenzo, da IBM, listou os seguintes requisitos para um computador quântico prático:

escalável fisicamente para aumentar o número de qubits
qubits pode ser inicializado com valores arbitrários
portas quânticas mais rápido do que tempo de decoerência
conjunto portão universal
qubits pode ser lido facilmente

Para resumir os problemas a partir da perspectiva de um engenheiro, é preciso resolver o desafio de construir um sistema que é isolado de tudo, exceto o mecanismo de medição e manipulação. Além disso, é necessário ser capaz de desligar o acoplamento dos qubits para a medição, de modo a não decohere qubits ao executar operações sobre eles.

Decoerência quântica

Um dos principais problemas é manter os componentes do computador num estado coerente, como a menor interacção com o mundo externo faria com que o sistema de decohere. Este efeito faz com que o personagem unitária (e, mais especificamente, a invertibilidade) de passos computacionais quânticos de ser violado. Decoherence vezes para sistemas candidatos, em particular, o tempo de relaxação transversal _T2 (na terminologia utilizada RMN e Tecnologia de ressonância magnética, também chamado de tempo dephasing), normalmente variam entre nanossegundos e segundo a baixa temperatura. A questão para abordagens ópticas são mais difíceis como estes prazos são ordens de magnitude inferior e uma abordagem frequentemente citado para superá-lo usa uma abordagem shaping pulso óptico. As taxas de erro são tipicamente proporcional à razão entre o tempo de funcionamento para o tempo decoherence, portanto, qualquer operação deve ser preenchido muito mais rapidamente do que o tempo decoherence.

Se a taxa de erro é suficientemente pequeno, pensa-se ser possível realizar a correcção de erro quântica, o qual corrige os erros devidos a decoherence, permitindo assim que o tempo de cálculo total a ser maior que o tempo do decoherence. Uma figura frequentemente citado (mas um tanto arbitrária) para a taxa de erro requerida em cada portão é de 10 ^-4. Isto implica que cada porta tem de ser capaz de desempenhar a sua tarefa 10.000 vezes mais rápida do que o tempo decoherence do sistema.

A concretização desta condição escalabilidade é possível para uma ampla variedade de sistemas. No entanto, a utilização de correcção de erro traz consigo o custo de um muito maior número de qubits necessários. O número necessário para o factor inteiros utilizando o algoritmo de Shor é ainda polinomial, e pensou-se entre L ² e L, onde L é o número de bits no número de ser tidos; algoritmos de correção de erro inflacionaria este valor por um fator adicional de L. Para um número 1000-bit, isso implica uma necessidade cerca de 10 ⁴ qubits sem correção de erros. Com a correção de erro, o valor subiria para cerca de 10 ⁷ qubits. Note-se que o tempo de cálculo é de cerca de 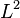$L ^ 2$ ou cerca de 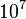$10 ^ 7$ passos e em 1 M Hz, cerca de 10 segundos.

Uma abordagem muito diferente para o problema de estabilidade decoherence-se para criar uma computador quântico topológico com anyons, quasi-partículas usadas como threads e contando com teoria trança para formar portas lógicas estáveis.

Candidatos

Há um número de candidatos a computação quântica, entre esses:

Superconductor baseados em computadores quânticos (incluindo SQUID baseada em computadores quânticos)
Ion preso computador quântico
Redes ópticas
Topológico computador quântico
Quantum dot na superfície (por exemplo, a Perda de DiVincenzo computador quântico)
Ressonância magnética nuclear em moléculas em solução (líquida RMN)
RMN de estado sólido Computadores quânticos Kane
Elétrons em computadores quânticos hélio
Eletrodinâmica quântica cavidade (CQED)
Ímã molecular
Baseado Fullerene- ESR computador quântico
Computadores quânticos baseados em óptica ( Óptica quântica)
Baseado-Diamond computador quântico
Computador quântico de Bose-Einstein baseada condensado
Cordas computadores quânticos com arrastamento de buracos positivos utilizando uma armadilha eletrostática - quantum computador baseado em transistores
Computador quântico baseado em rotação
Computação quântica adiabática

O grande número de candidatos mostra explicitamente que o tema, apesar de progressos rápidos, ainda está em sua infância. Mas, ao mesmo tempo, há também uma grande quantidade de flexibilidade.

Em 2005, pesquisadores da Universidade de Michigan construído um chip semicondutor , que funcionava como um ion trap. Tais dispositivos, produzidos pela norma técnicas de litografia, pode apontar o caminho para escaláveis ferramentas de computação quântica. Uma versão melhorada foi feita em 2006.

A computação quântica na teoria da complexidade computacional

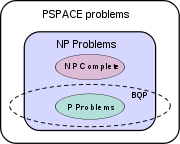
A relação suspeita de BQP para outros espaços problema.

Esta seção examina o que é conhecido atualmente matematicamente sobre o poder dos computadores quânticos. Ele descreve os resultados de conhecidos teoria e a complexidade computacional teoria da computação lidar com computadores quânticos.

A classe de problemas que podem ser resolvidos de forma eficiente por computadores quânticos é chamada BQP, por "erro limitada, quantum, tempo polinomial". Os computadores quânticos só correr algoritmos probabilísticos, então BQP em computadores quânticos é a contrapartida da BPP em computadores clássicos. É definida como o conjunto de problemas que podem ser resolvidos com um algoritmo de tempo polinomial, cuja probabilidade de erro é limitada a partir de um quarto. Um computador quântico é dito para "resolver" um problema se, para cada instância, a sua resposta será direita com alta probabilidade. Se essa solução é executado em tempo polinomial, então esse problema está em BQP.

BQP está contida na classe de complexidade #P (Ou mais precisamente na classe de problemas de decisão associado ^#P P), que é uma subclasse de PSPACE.

BQP é suspeito de ser separada de NP-completos e um super rigoroso de P, mas que não é conhecido. Tanto fatoração inteiro e log discreto estão em BQP. Ambos estes problemas são problemas NP que se suspeite estar fora BPP, e, portanto, fora P. Ambos são suspeitos de não ser NP-completo. Há um equívoco comum que os computadores quânticos pode resolver problemas NP-completos em tempo polinomial. Isso não é conhecido para ser verdade, e geralmente é suspeita de ser falsa.

Portões Quantum pode ser visto como transformações lineares. Daniel S. Abrams e Seth Lloyd têm mostrado que, se são permitidas transformações não lineares, então os problemas NP-completos poderia ser resolvido em tempo polinomial. Ele poderia até fazê-lo por # Problemas P-completos. Eles não acreditam que tal máquina é possível.

Embora computadores quânticos pode ser mais rápido do que os computadores clássicos, os descritos acima não podem resolver todos os problemas que os computadores clássicos não pode resolver, dado o tempo ea memória suficiente (embora possivelmente uma quantia que nunca poderia praticamente ser trazida para carregar). A Máquina de Turing pode simular estes computadores quânticos, assim que um computador quântico tal nunca poderia resolver um problema indecidível como o problema da parada. A existência de computadores quânticos "padrão" não desmente a Tese de Church-Turing.

Retirado de " http://en.wikipedia.org/w/index.php?title=Quantum_computer&oldid=227805628 "