Diagrama de Venn

Um diagrama de Venn de conjuntos A, B, e C

São diagramas de Venn ilustrações usadas no ramo da matemática conhecido como teoria dos conjuntos . Inventado em 1881 por John Venn, eles mostram todas as possíveis matemáticas ou lógicas relações entre conjuntos (grupos de coisas). Eles normalmente consistem de sobreposição de círculos . Por exemplo, em um conjunto de dois diagrama de Venn, um círculo pode representar todas as coisas que são líquidos à temperatura ambiente, enquanto outro círculo pode representar o conjunto de todos os elementos químicos. A área de sobreposição (intersecção), então representam coisas que são líquidos à temperatura ambiente e os elementos, por exemplo o mercúrio. Outros formatos podem ser utilizados (ver abaixo), e que isto é necessário para mais de três conjuntos.

Origins

Indicador de vidro manchado na sala de jantar de Gonville and Caius College, Cambridge

O Nasceu-Hull britânico filósofo e matemático John Venn (1834-1923) introduziu o diagrama de Venn em 1881 .

A janela de vitral em Caius College, Cambridge , onde estudou Venn e passou a maior parte de sua vida, comemora ele e representa um diagrama de Venn.

Exemplos

Conjuntos A e B

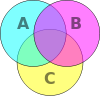
O círculo laranja ( Conjunto A) pode representar, por exemplo, todas as criaturas vivas que são de duas pernas. O círculo azul, (conjunto B) pode representar seres vivos que podem voar. A área onde os círculos azuis e alaranjados sobrepõem contém todas as criaturas vivas que podem voar e que têm duas pernas - por exemplo, os papagaios. (Imagine que cada tipo distinto de criatura como um ponto em algum lugar no diagrama.)

Os seres humanos e os pinguins seria no círculo laranja, na parte que não se sobrepõe com o círculo azul. Os mosquitos têm seis pernas, e voar, então o ponto de mosquitos seria na parte do círculo azul que não se sobrepõe com o laranja. Coisas que não são de duas pernas e não podem voar (por exemplo, as baleias e aranhas) seriam todos representados por pontos fora ambos os círculos. Tecnicamente, o diagrama de Venn acima pode ser interpretado como "as relações de conjunto A e B definida que pode ter alguns elementos (mas não todos) em comum".

A área combinada de conjuntos A e B é chamado o união de A e B, indicados por AUB. O sindicato, neste caso, contém todas as coisas que ou têm duas pernas, ou que voam, ou ambos.

A área em ambas, A e B, em que os dois conjuntos sobrepõem, é chamada a intersecção de A e B, indicados por A∩B. A intersecção dos dois conjuntos não está vazia, porque os círculos se sobrepõem, ou seja, não são criaturas que estão em ambos os círculos laranja e azul.

Às vezes um retângulo chamado de " Jogo universal "é desenhado em torno do diagrama de Venn para mostrar o espaço de todas as coisas possíveis. Como mencionado acima, uma baleia seria representado por um ponto que não está na união, mas é no Universo (dos seres vivos, ou de tudo coisas, dependendo de como um escolheu para definir o Universo para um diagrama particular).

Extensões para um maior número de conjuntos

Construção de Venn com n = 3

Construção de Venn com n = 4

Construção de Venn com n = 5

Construção de Venn com n = 6

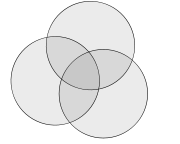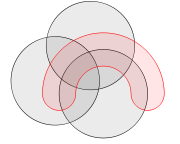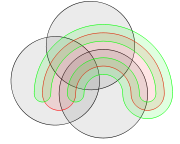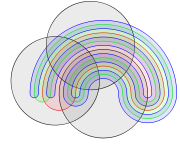Diagramas de Venn normalmente têm três sets. Venn estava ansioso para encontrar figuras simétricas ... elegante em si mesmos, o que representa um maior número de sets e ele concebeu um esquema de quatro set usando elipses . Ele também deu uma construção de diagramas de Venn com qualquer número de curvas, em que cada curva sucessiva é intercalada com curvas anteriores, começando com o esquema 3-círculo.

Simple Symmetric Diagramas de Venn

DW Henderson mostraram em 1963 que a existência de um diagrama -Venn n com n fold simetria rotacional implícito que n era nobre . Ele também mostrou que existem tais diagramas de Venn simétricas quando n é 5 ou 7. Em 2002 Peter Hamburger encontrados diagramas de Venn simétricas para n = 11 e, em 2003, Griggs, Killian, e Savage mostrou que os diagramas de Venn simétricas existem para todos os outros primos. Assim, os diagramas de Venn simétricas existe se e somente se n é um número primo.

Diagramas de Venn Edwards

Edwards 'diagrama de Venn de três sets	Edwards 'Diagrama de Venn das quatro conjuntos
Edwards 'diagrama de Venn de cinco sets	Edwards 'diagrama de Venn de seis conjuntos

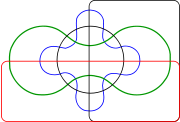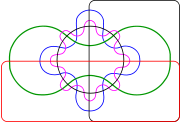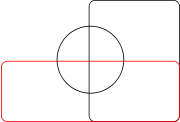
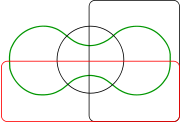
AWF Edwards deu uma construção para um maior número de jogos que oferece algumas simetrias. Sua construção é alcançada por projetar o diagrama de Venn em uma esfera . Três conjuntos podem ser facilmente representados por tomar três hemisférios em ângulos retos (x ≥0, y e z ≥0 ≥0). Um quarto conjunto pode ser representado pela tendo uma curva semelhante à costura sobre uma bola de ténis, que se estende para cima e para baixo em torno do equador. Os conjuntos resultantes podem então ser projectado para trás em relação ao plano da roda denteada para dar diagramas com o aumento do número de dentes. Esses diagramas foram criados ao projetar um vitral janela in memoriam ao Venn.

Outros diagramas

Diagramas de Venn Edwards são topologicamente equivalentes aos diagramas concebido por Branko Grünbaum que foram baseados em torno de interseção polígonos com um número crescente de lados. Eles também são representações 2-dimensionais de hypercubes.

Smith inventou diagramas n -conjunto semelhantes usando curvas seno com equações y = sin (2 x) ⁱ / 2 ^i, 0≤i≤ N -2.

Charles Lutwidge Dodgson (aka Lewis Carroll) elaborou um diagrama de cinco set.

Uso em sala de aula

Diagramas de Venn são muitas vezes utilizados pelos professores em sala de aula como um mecanismo para ajudar os alunos a comparar e contrastar dois itens. Características são listadas em cada seção do diagrama, com características compartilhadas listadas na seção de sobreposição.