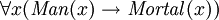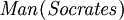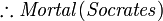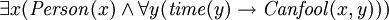Logique du premier ordre
Saviez-vous ...
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. enfants SOS est le plus grand don de charité du monde enfants orphelins et abandonnés la chance de la vie familiale.
Logique du premier ordre (FOL) est un formelle système déductif utilisé par les mathématiciens, des philosophes, des linguistes et des informaticiens. Il va par beaucoup de noms, y compris: premier ordre calcul des prédicats (FOPC), le calcul des prédicats inférieure, le langage de la logique du premier ordre ou de la logique des prédicats. Contrairement langues naturelles telles que l'anglais, FOL utilise un dépourvue de toute ambiguïté langage formel interprété par des structures mathématiques. FOL est un système de déduction étendant logique propositionnelle en permettant la quantification sur des individus d'un domaine donné (univers) du discours. Par exemple, il peut être indiqué dans FOL "Chaque individu a la propriété P".
Bien que logique propositionnelle traite des propositions déclaratives simples, logiques de premier ordre plus couvertures prédicats et la quantification. Prenez par exemple les phrases suivantes: "Socrate est un homme», «Platon est un homme". Dans la logique propositionnelle ces deux propositions seront indépendants, désignés par exemple par p et q. Dans la logique du premier ordre cependant, les deux peines seraient reliés par la même propriété: Man (x), où l'Homme (x) signifie que x est un homme. Lorsque x = Socrate nous obtenons la première proposition, p, et quand x = Platon nous obtenons la seconde proposition, q. Une telle construction permet une logique beaucoup plus puissant quand quantificateurs sont introduits, tels que "pour tout x ...", par exemple, "pour tout x, si l'Homme (x), alors ...". Sans quantificateurs, chaque argument valable dans FOL est valable dans la logique propositionnelle, et vice versa.
Une théorie du premier ordre se compose d'un ensemble de axiomes (généralement fini ou récursivement énumérable) et les états déductible de leur donner la relation de déductibilité sous-jacent. Habituellement ce qu'on entend par «théorie du premier ordre» est un certain ensemble d'axiomes ainsi que ceux d'un (et le son) axiomatisation complète de la logique du premier ordre, fermé en vertu des règles de FOL. (Tout système FOL donnera lieu à la même relation de déductibilité abstraite, donc nous ne avons pas besoin d'un système axiomatique fixe à l'esprit.) Un langage du premier ordre a le pouvoir expressif suffisante pour officialiser deux théories mathématiques importantes: ZFC la théorie des ensembles et Arithmétique de Peano. Un langage du premier ordre ne peut pas, cependant, exprimer catégoriquement la notion de responsabilisation, même si elle est exprimable dans la théorie du premier ordre sous la ZFC interprétation voulue pour le symbolisme de ZFC. Ces idées peuvent être exprimées avec catégoriquement logique du second ordre.
Pourquoi logique du premier ordre est nécessaire?
Logique propositionnelle ne est pas adéquat pour formaliser des arguments valables qui se appuient sur la structure interne des propositions concernées. Pour le voir, examiner la validité l'argument syllogistique:
- Tous les hommes sont mortels
- Socrate est un homme
- Par conséquent, Socrate est mortel
qui, lors de la traduction en propositionnel rendements logiques:
- Un
- B
 C
C
(Prise  pour signifier «donc»).
pour signifier «donc»).
Selon la logique propositionnelle, cette traduction ne est pas valide: logique propositionnelle valide arguments selon leur structure, et rien dans la structure de cet argument traduit (C résulte de A et B, pour arbitraire A, B, C) suggère qu'il est valide. Une traduction qui préserve la validité intuitive (et formelle) de l'argument doit prendre en considération la structure profonde de propositions, tels que les notions essentielles de la prédication et la quantification. Logique propositionnelle ne traite que de la vérité fonctionnelle validité: toute cession de valeurs de vérité aux variables de l'argument devrait soit la conclusion vrai ou au moins l'une des prémisses fausses. Il est clair que nous pouvons (uniforme) attribuer des valeurs de vérité aux variables de l'argument ci-dessus tel que A, B sont à la fois vrai, mais c est faux. D'où l'argument est la vérité fonctionnellement invalide. D'autre part, il est impossible de (uniforme) attribuer des valeurs de vérité à l'argument "Un découle de (A et B)" telle que (A et B) est vraie (d'où A est vrai et B est vrai) et un faux .
En revanche, cet argument peut être facilement traduit en logique du premier ordre:
(Où " 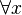 "Signifie" pour tout x ","
"Signifie" pour tout x ","  "Signifie" implique ",
"Signifie" implique ", 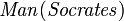 signifie «Socrate est un homme», et
signifie «Socrate est un homme», et 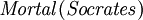 signifie «Socrate est mortel».) En clair, cela indique que
signifie «Socrate est mortel».) En clair, cela indique que
- pour tout x, si x est un homme alors x est mortel
- Socrate est un homme
- donc Socrate est mortel
FOL peut également exprimer l'existence de quelque chose ( 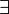 ), Ainsi que des prédicats («fonctions» qui sont vrai ou faux) avec plus d'un paramètre. Par exemple, "il ya quelqu'un qui peut être dupe chaque fois" peut être exprimée comme suit:
), Ainsi que des prédicats («fonctions» qui sont vrai ou faux) avec plus d'un paramètre. Par exemple, "il ya quelqu'un qui peut être dupe chaque fois" peut être exprimée comme suit:
Lorsque " 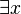 »Signifie« il existe (e) x ","
»Signifie« il existe (e) x "," 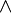 »Signifie« et », et
»Signifie« et », et 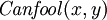 moyens "(personne) x peut être dupe (au moment) y".
moyens "(personne) x peut être dupe (au moment) y".
Définition premier ordre logique
Un calcul des prédicats se compose de
- règles de formation (c. Définitions récursives pour former formules bien formé).
- règles de transformation (c.-à- règles d'inférence pour dériver théorèmes).
- axiomes ou axiome schémas (éventuellement infini dénombrable).
Les axiomes considérés ici sont axiomes logiques qui font partie de FOL classique. Il est important de noter que FOL peut être formalisé dans de nombreuses manières équivalentes; il n'y a rien canonique sur les axiomes et les règles d'inférence fournies dans cet article. Il ya une infinité de formalisations équivalentes tous qui donnent les mêmes théorèmes et les non-théorèmes, et qui ont tous un droit égal vers le titre «FOL».
FOL est utilisé comme "bloc de construction" de base pour de nombreuses théories mathématiques. FOL propose plusieurs règles intégrées, telles que l'axiome 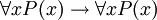 (Si P (x) est vraie pour tout x alors P (x) est vraie pour tout x). Axiomes non-logiques supplémentaires sont ajoutés pour produire théories de premier ordre spécifiques basés sur les axiomes de la FOL classique; ces théories construites sur FOL sont appelés théories classiques de premier ordre. Un exemple d'une théorie du premier ordre classique est Arithmétique de Peano, qui ajoute l'axiome
(Si P (x) est vraie pour tout x alors P (x) est vraie pour tout x). Axiomes non-logiques supplémentaires sont ajoutés pour produire théories de premier ordre spécifiques basés sur les axiomes de la FOL classique; ces théories construites sur FOL sont appelés théories classiques de premier ordre. Un exemple d'une théorie du premier ordre classique est Arithmétique de Peano, qui ajoute l'axiome 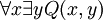 (Ce est à dire pour tout x il existe y tel que y = x + 1, où Q (x, y) est interprétée comme "y = x + 1"). Cet axiome supplémentaire est un axiome non-logique; il ne est pas partie de FOL, mais est un axiome de la théorie (un axiome de l'arithmétique plutôt que de la logique). Axiomes de ce dernier type sont également appelés axiomes de théories de premier ordre. Les axiomes de théories de premier ordre ne sont pas considérés comme des vérités de la logique en soi, mais plutôt comme des vérités de la théorie particulière qui a généralement associé à une interprétation prévue de ses symboles non logiques. (Voir une idée analogue à logique par rapport symboles non-logique.) Ainsi, l'axiome à propos de Q (x, y) ne est vrai que l'interprétation de la relation Q (x, y) comme «y = x + 1", et seulement dans la théorie de Arithmétique de Peano. FOL classique ne ont associé à une interprétation destinée de son vocabulaire non-logique (sauf sans doute un symbole désignant l'identité, selon que l'on considère un tel symbole que logique). classique théorie des ensembles est un autre exemple d'une théorie du premier ordre (une théorie construite sur FOL).
(Ce est à dire pour tout x il existe y tel que y = x + 1, où Q (x, y) est interprétée comme "y = x + 1"). Cet axiome supplémentaire est un axiome non-logique; il ne est pas partie de FOL, mais est un axiome de la théorie (un axiome de l'arithmétique plutôt que de la logique). Axiomes de ce dernier type sont également appelés axiomes de théories de premier ordre. Les axiomes de théories de premier ordre ne sont pas considérés comme des vérités de la logique en soi, mais plutôt comme des vérités de la théorie particulière qui a généralement associé à une interprétation prévue de ses symboles non logiques. (Voir une idée analogue à logique par rapport symboles non-logique.) Ainsi, l'axiome à propos de Q (x, y) ne est vrai que l'interprétation de la relation Q (x, y) comme «y = x + 1", et seulement dans la théorie de Arithmétique de Peano. FOL classique ne ont associé à une interprétation destinée de son vocabulaire non-logique (sauf sans doute un symbole désignant l'identité, selon que l'on considère un tel symbole que logique). classique théorie des ensembles est un autre exemple d'une théorie du premier ordre (une théorie construite sur FOL).
Vocabulaire
Avant mise en place des règles de formation, il faut décrire la "vocabulaire", qui se compose de
- Un ensemble de variables sous-jacentes (ou relations) chacun avec une certaine valence (ou arité, nombre de ses arguments) ≥1, qui sont souvent désignés par des lettres majuscules P, Q, R, ....
- Par exemple, P (x) est un prédicat variables de valence 1. Il peut se tenir pour "x est un homme", par exemple.
- Q (x, y) est un prédicat variables de valence 2. Il peut se tenir pour "x est supérieur à y" en arithmétique ou "x est le père de y", par exemple.
- Il est possible de permettre aux relations de valence 0; ceux-ci peuvent être considérées comme variables propositionnelles. Par exemple, P, qui peut se tenir pour toute déclaration.
- En utilisant les fonctions (voir ci-dessous), il est possible de se passer de toutes les variables sous-jacentes avec valence supérieur à un. Par exemple, "x> y» (un prédicat de valence 2, du type Q (x, y)) peuvent être remplacés par un prédicat de valence 1 à propos de la couple (x, y).
- Un ensemble de constantes, souvent désigné par les lettres minuscules au début de l'alphabet a, b, c, ....
- Exemples: un peut tenir pour Socrates. En arithmétique , il peut se présenter à 0. En théorie des ensembles , un tel constante peut tenir pour le ensemble vide.
- Un ensemble de fonctions, chacune d'un certain valence ≥ 1, qui sont souvent désignée par les lettres minuscules f, g, h, ....
- Exemples: f (x) peuvent se présenter "le père de x". En arithmétique , on peut tenir pour "-x". En théorie des ensembles , il peut signifier «la ensemble des x de puissance ". En arithmétique , f (x, y) peut signifier «x + y". En théorie des ensembles , il peut se présenter à «l'union de x et y".
- Une constante est vraiment une fonction de valence 0. Cependant il est de tradition d'utiliser le terme «fonction» que pour des fonctions de valence au moins une.
- On peut en principe renoncer entièrement aux fonctions d'arité> 2 et prédicats d'arité> 1 se il est un symbole de fonction d'arité 2 représentant un paire ordonnée (ou symboles de prédicat d'arité 2 représentant les relations de projection d'un paire ordonnée). La paire ou projections doivent satisfaire les axiomes naturels.
- On peut en principe renoncer entièrement aux fonctions et constantes. Par exemple, au lieu d'utiliser une constante 0, on peut utiliser un prédicat 0 (x) (interprété comme "x = 0"), et de remplacer chaque prédicat tel que P (0, y)
 x 0 (x)
x 0 (x)  P (x, y). Une fonction telle que f (x1, x2 ...) comportera aussi être remplacé par un prédicat F (x1, x2 ..., y) (interprété comme "y = f (x1, x2 ...)").
P (x, y). Une fonction telle que f (x1, x2 ...) comportera aussi être remplacé par un prédicat F (x1, x2 ..., y) (interprété comme "y = f (x1, x2 ...)").
- Un ensemble infini de variables, souvent désigné par les lettres minuscules à la fin de l'alphabet x, y, z, ....
- Symboles désignant les opérateurs logiques (ou connecteurs):
 ( logique de ne pas),
( logique de ne pas),  ( conditionnelle logique).
( conditionnelle logique).  (Φ
(Φ 
 ψ) est logiquement équivalente à φ
ψ) est logiquement équivalente à φ  ψ ( et logique). φ
ψ ( et logique). φ  ψ peut être considéré comme un raccourci pour cela. Alternativement, on peut ajouter le
ψ peut être considéré comme un raccourci pour cela. Alternativement, on peut ajouter le  symbole comme un opérateur logique au vocabulaire et axiomes appropriés.
symbole comme un opérateur logique au vocabulaire et axiomes appropriés.  φ
φ  ψ est logiquement équivalente à φ
ψ est logiquement équivalente à φ  ψ ( ou logique). φ
ψ ( ou logique). φ  ψ peut être considéré comme un raccourci pour cela. Alternativement, on peut ajouter le
ψ peut être considéré comme un raccourci pour cela. Alternativement, on peut ajouter le 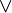 symbole comme un opérateur logique au vocabulaire et axiomes appropriés.
symbole comme un opérateur logique au vocabulaire et axiomes appropriés. - De même, (φ
 ψ)
ψ)  (Ψ
(Ψ  φ) est logiquement équivalente à φ
φ) est logiquement équivalente à φ 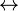 ψ ( biconditional logique), et l'on peut utiliser ce dernier comme un raccourci pour cela, ou encore ajouter ceci à le vocabulaire et ajouter axiomes appropriés. Parfois φ
ψ ( biconditional logique), et l'on peut utiliser ce dernier comme un raccourci pour cela, ou encore ajouter ceci à le vocabulaire et ajouter axiomes appropriés. Parfois φ 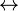 ψ est écrit que φ
ψ est écrit que φ  ψ.
ψ.
- Symboles indiquant quantificateurs:
 ( quantification universelle, généralement lire comme «pour tous»).
( quantification universelle, généralement lire comme «pour tous»). 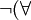 x
x  φ) est logiquement équivalent à
φ) est logiquement équivalent à 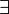 x φ ( quantification existentielle, généralement lire comme "il existe"). Ce dernier peut soit être utilisé comme un raccourci pour cela, ou ajouté au vocabulaire avec axiomes appropriés.
x φ ( quantification existentielle, généralement lire comme "il existe"). Ce dernier peut soit être utilisé comme un raccourci pour cela, ou ajouté au vocabulaire avec axiomes appropriés.
- Gauche et parenthèse droite.
- Il existe de nombreuses conventions différentes sur où mettre entre parenthèses; par exemple, on pourrait écrire
 ou x (
ou x (  x). Parfois, on utilise deux points ou des arrêts complets au lieu de parenthèses pour faire formules sans ambiguïté. Une convention intéressante, mais est plutôt inhabituel " Notation polonaise ", où l'on omet tous les parenthèses, et écrit
x). Parfois, on utilise deux points ou des arrêts complets au lieu de parenthèses pour faire formules sans ambiguïté. Une convention intéressante, mais est plutôt inhabituel " Notation polonaise ", où l'on omet tous les parenthèses, et écrit  ,
,  Et ainsi de suite devant leurs arguments non entre eux. Notation polonaise est compact et élégant, mais rare parce qu'il est difficile pour les humains de le lire.
Et ainsi de suite devant leurs arguments non entre eux. Notation polonaise est compact et élégant, mais rare parce qu'il est difficile pour les humains de le lire.
- Il existe de nombreuses conventions différentes sur où mettre entre parenthèses; par exemple, on pourrait écrire
- Un symbole de l'identité ou de l'égalité = est parfois, mais pas toujours inclus dans le vocabulaire.
- Si l'égalité est considérée comme une partie de la logique du premier ordre, le symbole de l'égalité comporte syntaxiquement comme un prédicat binaire. Ce cas est parfois appelé logique du premier ordre avec égalité.
Il existe plusieurs autres variations mineures dans la liste ci-dessous:
- L'ensemble des symboles primitifs (opérateurs et quantificateurs) varie souvent. Il est possible d'inclure d'autres opérateurs primitifs, tels que
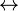 (FIF),
(FIF),  (B) et
(B) et 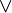 (Ou), la vérité constantes T pour "true" et F pour "false" (ce sont les opérateurs de valence 0), et / ou de la Sheffer course (P | Q, alias NAND). Le nombre minimum de symboles primitifs nécessaires est une, mais si nous nous limitons aux opérateurs énumérés ci-dessus, nous avons besoin de trois, comme ci-dessus.
(Ou), la vérité constantes T pour "true" et F pour "false" (ce sont les opérateurs de valence 0), et / ou de la Sheffer course (P | Q, alias NAND). Le nombre minimum de symboles primitifs nécessaires est une, mais si nous nous limitons aux opérateurs énumérés ci-dessus, nous avons besoin de trois, comme ci-dessus. - Certains livres et papiers utilisent φ de notation
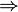 ψ pour φ
ψ pour φ  ψ. Cela est particulièrement vrai en théorie preuve lorsque
ψ. Cela est particulièrement vrai en théorie preuve lorsque  est facilement confondu avec la flèche de séquent. On voit aussi ~ φ pour
est facilement confondu avec la flèche de séquent. On voit aussi ~ φ pour  φ, φ et ψ pour φ
φ, φ et ψ pour φ  ψ, et une richesse de notations pour quantificateurs; par exemple,
ψ, et une richesse de notations pour quantificateurs; par exemple,  x φ peut se écrire (x) φ. Cette dernière annotation est commun dans les textes sur la théorie de la récursivité.
x φ peut se écrire (x) φ. Cette dernière annotation est commun dans les textes sur la théorie de la récursivité. - Il est souvent plus facile dans la pratique d'utiliser une notation simple qui prend en charge les opérateurs infixes et omet parenthèses inutiles. Ainsi, si P est une relation de valence 2, nous écrivons souvent «P ab" "P b" au lieu de; par exemple, nous écrivons une <2 au lieu de <(1 2). De même, si f est une fonction de valence 2, nous écrivons parfois "AFB" au lieu de "f (ab)"; par exemple, nous écrivons 1 + 2 au lieu de + (1 2). Par convention, les opérateurs infixes ont tendance à utiliser des noms de fonction non alphabétiques. Il est également courant d'omettre certains parenthèses si cela ne conduit pas à l'ambiguïté (conduisant à la définition d'une priorité).
- Il est parfois utile de dire que "P (x) est vérifiée pour exactement une x", qui peut être exprimé sous la forme
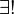 x P (x). Cette notation ne peut être prise pour abréger une formule telle que
x P (x). Cette notation ne peut être prise pour abréger une formule telle que 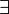 x (P (x)
x (P (x) 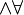 y (P (y)
y (P (y)  (X = y))).
(X = y))).
Les programmes informatiques qui acceptent de premier ordre représentations logiques seront généralement accepter au moins ces quantificateurs et les opérateurs (même se ils peuvent utiliser différents symboles pour les représenter):  (Pour tous),
(Pour tous), 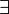 (Existe),
(Existe),  (Non),
(Non),  (Et),
(Et), 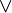 (Ou),
(Ou),  (Implique), et
(Implique), et 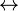 (Si et seulement si). Le exclusif ou l'exploitant "XOR" est également fréquente.
(Si et seulement si). Le exclusif ou l'exploitant "XOR" est également fréquente.
Les ensembles de constantes, les fonctions et les relations sont normalement considérés comme formant une langue, tandis que les variables, les opérateurs logiques, et quantificateurs sont généralement considérés comme appartenant à la logique. Par exemple, le langage de la théorie de groupe se compose d'une constante (l'élément d'identité), une fonction de valence 1 (l'inverse) une fonction de valence 2 (le produit), et une relation de valence 2 (égalité), qui serait omis par des auteurs qui incluent l'égalité dans la logique sous-jacente.
règles de Formation
Les règles de formation définissent les termes et formules de logique du premier ordre. Lorsque termes et formules sont représentées comme des chaînes de symboles, ces règles peuvent être utilisées pour écrire un grammaire formelle pour les termes et formules. Le concept de variable libre est utilisé pour définir des phrases en tant que sous-ensemble des formules.
Termes
L'ensemble des termes est récursive définies par les règles suivantes:
- Toute constante est un terme.
- Toute variable est un terme.
- Toute expression f (t 1, ..., t n) de n ≥ 1 arguments (où chaque argument t i est un terme et f est un symbole de fonction de valence n) est un terme.
- clause de Fermeture: Rien d'autre ne est un terme. Par exemple, les prédicats sont pas des termes.
Formules
L'ensemble des formules bien formées (généralement appelés s WFF ou tout simplement formules) est récursive définies par les règles suivantes:
- Prédicats simples et complexes Si P est une relation de valence n ≥ 1 et les a i sont des termes alors p (a 1, ..., a n) est bien formé. Si l'égalité est considérée comme faisant partie de la logique, alors (a 1 = 2) est bien formée. Toutes ces formules sont dites atomique.
- Clause inductif I: Si φ est une wff, puis
 φ est un wff.
φ est un wff. - Clause inductif II: Si φ et ψ sont s WFF, alors (φ
 ψ) est une wff.
ψ) est une wff. - Clause inductive III: Si φ est une wff et x est une variable,
 x φ est un wff.
x φ est un wff. - Fermeture article: Rien d'autre ne est un wff.
Par exemple,  x
x  y (P (f (x))
y (P (f (x)) 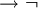 (P (x)
(P (x)  Q (f (y), x, z))) est une formule bien formé, si f est une fonction de valence 1, P un prédicat de valence 1 et Q un prédicat de valence 3.
Q (f (y), x, z))) est une formule bien formé, si f est une fonction de valence 1, P un prédicat de valence 1 et Q un prédicat de valence 3.  xx
xx  ne est pas une formule bien formée.
ne est pas une formule bien formée.
Dans la science informatique terminologie, une formule implémente un type "booléen" intégré, tandis qu'un terme met en œuvre tous les autres types.
Variables libres et liés
- Formules atomiques Si φ est une formule atomique alors X est libre dans φ si et seulement si x se produit dans φ.
- Inductif article I: x est libre dans
 φ si et seulement si x est libre dans φ.
φ si et seulement si x est libre dans φ. - Clause inductif II: x est libre dans (φ
 ψ) si et seulement si x est libre dans φ et ne se produit pas dans ψ, ou x est libre dans ψ et ne se produit pas dans φ, ou x est libre à la fois φ et ψ.
ψ) si et seulement si x est libre dans φ et ne se produit pas dans ψ, ou x est libre dans ψ et ne se produit pas dans φ, ou x est libre à la fois φ et ψ. - Clause inductive III: x est libre dans
 y φ si et seulement si x est libre dans φ et x est un symbole différent de y.
y φ si et seulement si x est libre dans φ et x est un symbole différent de y. - Fermeture article: x est lié dans φ si et seulement si x se produit dans φ et x ne est pas libre dans φ.
- Par exemple, dans
 x
x  y (P (x)
y (P (x)  Q (x, f (x), z) de variables), X et Y sont liés, z est une variable libre, et w ne est pas, car il ne se produit pas dans la formule.
Q (x, f (x), z) de variables), X et Y sont liés, z est une variable libre, et w ne est pas, car il ne se produit pas dans la formule.
Exemple
En mathématiques la langue de groupes abéliens ordonnés a une constante 0, une fonction unaire -, une fonction binaire +, et une relation binaire ≤. Donc:
- 0, x, y sont des termes atomiques
- + (X, y) + (x, + (y, - (z))) sont termes, habituellement écrit x + y, x + y - z
- = (+ (X, y), 0) ≤ (+ (x, + (y, - (z))) + (x, y)) sont des formules atomiques, habituellement écrit comme x + y = 0, x Y + - z ≤ x + y,
- (
 x
x  y ≤ (+ (x, y), z))
y ≤ (+ (x, y), z))  (
(  x = (+ (x, y), 0)) est une formule, généralement écrit comme (
x = (+ (x, y), 0)) est une formule, généralement écrit comme (  x
x  y x + y ≤ z)
y x + y ≤ z)  (
(  x x + y = 0).
x x + y = 0).
Substitution
Si t est un terme et φ (x) est une formule contenant éventuellement des x en tant que variable libre, puis φ (t) est défini comme étant le résultat de remplacer toutes les occurrences libres de x par t, à condition que pas variable libre de t devient lié à ce processus. Si une variable libre de t est lié, puis t remplacer x il est d'abord nécessaire de changer les noms des variables liées de φ à autre chose que les variables libres de t.
Pour voir pourquoi cette condition est nécessaire, envisager la formule φ (x) donnée par  y y x ≤ ("x est maximale»). Si t est un terme sans y comme une variable libre, alors φ (t) signifie simplement t est maximale. Cependant, si t est l'y φ de formule (y) est
y y x ≤ ("x est maximale»). Si t est un terme sans y comme une variable libre, alors φ (t) signifie simplement t est maximale. Cependant, si t est l'y φ de formule (y) est  y y ≤ y qui ne dit pas que y est maximale. Le problème est que la variable y libre de t (= y) est devenu lié quand nous avons substitué pour Y x dans φ (x). Donc, pour φ (y) former nous devons d'abord changer la variable liée y de φ à autre chose, dire z, de sorte que φ (y) est alors
y y ≤ y qui ne dit pas que y est maximale. Le problème est que la variable y libre de t (= y) est devenu lié quand nous avons substitué pour Y x dans φ (x). Donc, pour φ (y) former nous devons d'abord changer la variable liée y de φ à autre chose, dire z, de sorte que φ (y) est alors  z z ≤ y. Oubliant cette condition est une cause notoire d'erreurs.
z z ≤ y. Oubliant cette condition est une cause notoire d'erreurs.
Les règles d'inférence
Une règle d'inférence est une fonction à partir d'ensembles de (bien formés) formules, appelé locaux, à des ensembles de formules appelées conclusions. Dans les systèmes déductifs les plus connus, les règles d'inférence prennent un ensemble de formules à une seule conclusion. (Notez que ce est vrai même dans le cas de la plupart séquent calculs.)
Les règles d'inférence sont utilisées pour prouver des théorèmes , qui sont prouvables en matière de formules ou des membres d'une théorie. Si le locaux d'une règle d'inférence sont des théorèmes, sa conclusion est un théorème ainsi. En d'autres termes, les règles d'inférence sont utilisées pour générer des «nouveaux» théorèmes de «anciens» - ils sont theoremhood préservent. Systèmes pour les théories de génération sont souvent appelés calculs jacentes. Elles sont décrites dans une section ci-dessous.
Une règle d'inférence importante, modus ponens, stipule que si φ et φ  ψ sont deux théorèmes, alors ψ est un théorème. Ceci peut se écrire de la manière suivante;
ψ sont deux théorèmes, alors ψ est un théorème. Ceci peut se écrire de la manière suivante;
- si
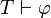 et
et 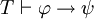 , Puis
, Puis 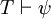
où 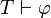 indique
indique 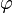 est prouvable en théorie T. Il existe des systèmes déductifs (connus sous le nom Hilbert-style systèmes déductifs) dans lequel modus ponens est la seule règle d'inférence; dans de tels systèmes, l'absence d'autres règles d'inférence est compensée avec une abondance de régimes d'axiomes logiques.
est prouvable en théorie T. Il existe des systèmes déductifs (connus sous le nom Hilbert-style systèmes déductifs) dans lequel modus ponens est la seule règle d'inférence; dans de tels systèmes, l'absence d'autres règles d'inférence est compensée avec une abondance de régimes d'axiomes logiques.
Une deuxième règle d'inférence est importante Généralisation universelle. On peut affirmer que
- si
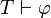 , Puis
, Puis 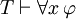
Qui se lit: si φ est un théorème, puis "pour tout x, φ" est un théorème ainsi. Le schéma d'aspect semblable 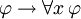 ne est pas saine, en général, même si elle ne dispose cependant instances valides, comme lorsque x ne est pas libre dans φ (voir Généralisation (logique)).
ne est pas saine, en général, même si elle ne dispose cependant instances valides, comme lorsque x ne est pas libre dans φ (voir Généralisation (logique)).
Axiomes
Ici suit une description des axiomes de la logique du premier ordre. Comme expliqué ci-dessus, une théorie donnée de premier ordre, a d'autres axiomes non-logiques. Les axiomes logiques suivants caractérisent un calcul des prédicats pour l'exemple de cet article de la logique du premier ordre.
Pour une quelconque théorie, il est intéressant de savoir si l'ensemble des axiomes peut être généré par un algorithme, ou se il existe un algorithme qui détermine si une formule bien formée est un axiome.
Se il ya un algorithme pour générer tous les axiomes, alors l'ensemble des axiomes est dit récursivement énumérable.
Se il est un algorithme qui détermine après un nombre fini d'étapes si une formule est un axiome ou non, alors l'ensemble des axiomes est dit récursif ou décidable. Dans ce cas, on peut aussi construire un algorithme pour générer tous les axiomes: cet algorithme se appuie tout simplement toutes les formules possibles un par un (d'une longueur de plus en plus), et pour chaque formule l'algorithme détermine si ce est un axiome.
Axiomes de la logique du premier ordre sont toujours décidable. Cependant, dans une théorie du premier ordre axiomes non-logiques ne sont pas nécessairement tel.
axiomes de quantificateurs
axiomes de quantificateurs changent en fonction de la façon dont le vocabulaire est défini, comment la procédure de remplacement fonctionne, quelles sont les règles de formation et dont les règles d'inférence sont utilisés. Ici suit un exemple précis de ces axiomes
- PRED-1:
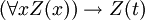
- PRED-2:
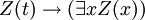
- PRED-3:
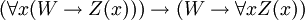
- PRED-4:
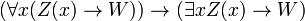
Ce sont en fait axiome schémas: l'expression W représente tout wff dans laquelle x ne est pas libre, et l'expression Z (x) signifie toute wff à la convention additionnelle que Z (t) représente le résultat de la substitution du terme t pour x dans Z (x). Ainsi, ce est un ensemble récursif d'axiomes.
Un autre axiome, 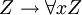 , Pour Z dans laquelle x ne se produit pas, est parfois ajouté.
, Pour Z dans laquelle x ne se produit pas, est parfois ajouté.
Egalité et ses axiomes
Il existe plusieurs conventions différentes pour l'utilisation de l'égalité (ou l'identité) dans la logique du premier ordre. Cette section résume les principales. Les différentes conventions donnent tous essentiellement les mêmes résultats avec environ la même quantité de travail, et diffèrent principalement dans la terminologie.
- La convention la plus courante pour l'égalité est d'inclure le symbole de l'égalité comme un symbole logique primitive, et ajouter les axiomes pour l'égalité aux axiomes de la logique du premier ordre. Les axiomes d'égalité sont
- x = x
- x = y → f (..., x, ...) = f (..., y, ...) pour toute fonction f
- x = y → (P (..., x, ...) → P (..., y, ...)) pour toute relation P (y compris la relation d'égalité elle-même)
- Ce sont, aussi, axiome schémas: ils définissent un algorithme qui décide si une formule donnée est un axiome. Ainsi, ce est un ensemble récursif d'axiomes.
- La prochaine convention la plus courante consiste à inclure le symbole de l'égalité comme une des relations d'une théorie, et ajouter les axiomes d'égalité aux axiomes de la théorie. En pratique, cela est presque impossible à distinguer de la convention précédente, sauf dans le cas inhabituel de théories sans notion d'égalité. Les axiomes sont les mêmes, et la seule différence est que l'on appelle certains d'entre eux axiomes ou axiomes de la théorie logiques.
- Dans les théories sans fonctions et un nombre fini de relations, il est possible de définir l'égalité en termes de relations, en définissant les deux termes s et t d'être égaux si toute relation est inchangée en changeant s à t dans ne importe quel argument.
- Par exemple, dans la théorie des ensembles avec une relation
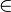 , Nous pouvons définir s = t être une abréviation pour
, Nous pouvons définir s = t être une abréviation pour  x (s
x (s 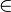 x
x 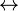 t
t 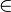 x)
x) 
 x (x
x (x 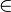 s
s 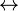 x
x 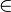 t). Cette définition de l'égalité satisfait alors automatiquement les axiomes pour l'égalité.
t). Cette définition de l'égalité satisfait alors automatiquement les axiomes pour l'égalité. - Sinon, si l'on ne utilise le symbole de l'égalité comme une relation de la théorie ou de la logique, il faudrait alors ajouter des axiomes. Dans l'exemple précédent, il faudrait ajouter l'axiome
 s
s  t (
t (  x (x
x (x 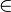 s
s 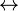 x
x 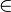 t))
t))  s = t.
s = t.
- Par exemple, dans la théorie des ensembles avec une relation
- Dans certaines théories, il est possible de donner des définitions ad hoc de l'égalité. Par exemple, dans une théorie des ordres partiels avec une relation ≤ nous pourrions définir s = t être une abréviation pour s ≤ t
 t ≤ s.
t ≤ s.
Calcul des prédicats
Le calcul des prédicats est une bonne extension de la calcul propositionnel, qui détermine les déclarations de la logique du premier ordre sont démontrables. Un grand nombre (mais pas tous) théories mathématiques peuvent être formulées dans le calcul des prédicats. Si le calcul propositionnel est définie par un ensemble approprié d'axiomes et de la règle unique de l'inférence modus ponens (ce qui peut être fait de plusieurs façons), puis le calcul des prédicats peuvent être définies en ajoutant le calcul des propositions de plusieurs axiomes et de la règle d'inférence appelée «généralisation universelle". Comme axiomes pour le calcul des prédicats nous prenons:
- Tous les tautologies du calcul des propositions, prises schématiquement sorte que le remplacement uniforme d'une lettre par une formule schématique est autorisé.
- Les axiomes de quantificateurs, donnés ci-dessus.
- Les axiomes ci-dessus pour l'égalité, si l'égalité est considérée comme un concept logique.
Une phrase est défini pour être prouvable en logique du premier ordre se il peut être déduit des axiomes du calcul des prédicats, en appliquant de façon répétée les règles d'inférence "modus de Ponens» et «généralisation universelle". Autrement dit:
- Un axiome du calcul des prédicats est prouvable en logique du premier ordre par définition.
- Si le locaux d'une règle d'inférence sont prouvable en logique du premier ordre, alors il en est de son conclusion.
Si nous avons une théorie T (un ensemble d'énoncés, appelés axiomes, dans une langue) alors φ de phrase est défini pour être prouvable dans la théorie T si
est prouvable en logique du premier ordre, pour un certain ensemble fini d'axiomes 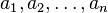 de la théorie T. En d'autres termes, si l'on peut prouver dans la logique du premier ordre φ découle des axiomes de T. Cela signifie aussi que l'on remplace la procédure ci-dessus pour trouver des phrases prouvables par la suivante:
de la théorie T. En d'autres termes, si l'on peut prouver dans la logique du premier ordre φ découle des axiomes de T. Cela signifie aussi que l'on remplace la procédure ci-dessus pour trouver des phrases prouvables par la suivante:
- Un axiome de T est prouvable dans T.
- Un axiome du calcul des prédicats est prouvable dans T.
- Si le locaux d'une règle d'inférence sont prouvable dans T, alors il en est de son conclusion.
Un problème apparent avec cette définition de prouvabilité est qu'il semble plutôt ad hoc: nous avons pris un certain collection apparemment aléatoire d'axiomes et de règles d'inférence, et il ne est pas clair que nous ne avons pas accidentellement manqué quelque axiome ou une règle essentielle. Théorème de complétude de Gödel nous assure que ce ne est pas vraiment un problème: tout énoncé vrai dans tous les modèles (sémantiquement vrais) est prouvable en logique du premier ordre (syntaxiquement vrai). En particulier, toute définition raisonnable de "prouvable" dans la logique du premier ordre doit être équivalent à celui ci-dessus (se il est possible pour les longueurs d'épreuves diffèrent considérablement pour différentes définitions de prouvabilité).
Il ya plusieurs façons différentes (mais équivalents) pour définir prouvabilité. La définition ci-dessus est typique pour un calcul "de style Hilbert", qui a de nombreux axiomes, mais très peu de règles d'inférence. En revanche, un «Style Gentzen" calcul des prédicats a quelques axiomes mais beaucoup de règles d'inférence.
Identités prouvables
Les phrases suivantes peuvent être appelées «identités» parce que le conjonctif dans chaque principale est la biconditional. Ils sont tous prouvable en FOL, et sont utiles lors de la manipulation des quantificateurs:
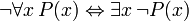
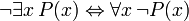
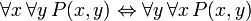
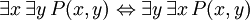
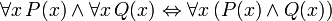
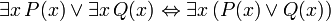
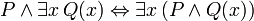 (Où
(Où 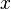 ne doit pas se produire gratuitement
ne doit pas se produire gratuitement 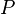 )
) 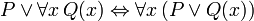 (Où
(Où 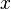 ne doit pas se produire gratuitement
ne doit pas se produire gratuitement 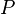 )
)
Règles d'inférence prouvables
Le principal conjonctif dans les phrases suivantes, aussi prouvable en FOL, est le conditionnelle. Ces peines peuvent être considérés comme la justification de règles d'inférence en plus modus ponens et la généralisation universelle discutés ci-dessus et dont la validité:
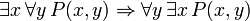
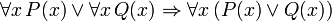
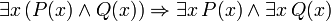
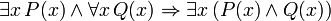
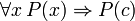 (Si c est une variable, alors il ne doit pas être quantifié précédemment dans P (x))
(Si c est une variable, alors il ne doit pas être quantifié précédemment dans P (x)) 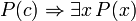 (Il doit y avoir aucune instance libre de x dans P (c))
(Il doit y avoir aucune instance libre de x dans P (c))
Théorèmes métalogiques de logique du premier ordre
Certains théorèmes métalogiques importants sont listés ci-dessous sous forme puces. Ce qu'ils veulent dire à peu près, ce est que la peine est valide si et seulement si elle est prouvable. En outre, on peut construire un algorithme qui fonctionne comme suit: si une phrase est prouvable, l'algorithme va nous dire que, dans une quantité finie, mais de temps inconnue. Si une phrase est indémontrable, l'algorithme fonctionnera toujours, et nous ne saurons pas si la peine est indémontrable ou démontrable et l'algorithme que nous a tout simplement pas encore dit. Un tel algorithme est appelé semidecidable ou récursivement énumérable.
On peut construire un algorithme qui va déterminer en nombre fini d'étapes si une peine est prouvable (un algorithme décidable) que pour les classes simples de la logique du premier ordre.
- Le problème de décision pour la validité est récursivement énumérable; en d'autres termes, il existe un Machine de Turing que lorsque donné aucune phrase comme entrée, se arrête si et seulement si la phrase est valable (vrai dans tous les modèles).
- Comme Exhaustivité théorème de Gödel les spectacles, pour toute formule valide P, P est prouvable. Inversement, en supposant que la cohérence de la logique, toute formule démontrable est valide.
- La machine de Turing peut être un composé qui génère toutes les formules démontrables de la manière suivante: pour un fini ou récursive ensemble dénombrable d'axiomes, une telle machine peut être celui qui génère un axiome, puis génère une nouvelle formule prouvable par l'application d'axiomes et de règles d'inférence déjà générés, puis générer un autre axiome, et ainsi de suite. Compte tenu d'une phrase comme entrée, la machine de Turing aller simplement sur et génère toutes les formules prouvables un par un, et se arrête si elle génère la phrase.
- Contrairement à la la logique propositionnelle, la logique du premier ordre est indécidable, à condition que la langue a au moins un prédicat de valence au moins deux autres que l'égalité. Cela signifie qu'il n'y a pas procédure de décision qui détermine correctement si une formule arbitraire est valide. Parce qu'il est une machine de Turing comme décrit ci-dessus, le indécidabilité est lié à l'insolubilité de la Problème de l'arrêt: existe pas d'algorithme qui détermine après un nombre fini d'étapes si la machine de Turing sera jamais halte pour une phrase donnée en entrée, par conséquent, si la phrase est prouvable. Ce résultat a été établi indépendamment par Église et Turing .
- La logique des prédicats Monadique (c.-à-logique des prédicats avec seulement un argument de prédicats et pas de fonctions) est décidable.
- Le Classe Bernays-Schönfinkel de formules du premier ordre est également décidable.
Traduire langage naturel à la logique du premier ordre
Concepts exprimées en langage naturel doivent être «traduits» à la logique du premier ordre (FOL) avant FOL peut être utilisé pour y faire face, et il ya un certain nombre de pièges potentiels dans cette traduction. Dans FOL, 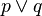 signifie "p, ou q, ou les deux", autrement dit, il est inclus. En anglais, le mot «ou» est parfois inclus (par exemple, "la crème ou de sucre?»), Mais il est parfois exclusive (par exemple, "café ou de thé?" Est généralement destiné à signifier un ou l'autre, pas les deux). De même, le mot anglais «certains» peut signifier «au moins un, peut-être tous", mais d'autres fois, cela peut signifier "pas tous, peut-être pas". Le mot anglais "et" doit parfois être traduit par "ou" (par exemple, "les hommes et les femmes peuvent se appliquer").
signifie "p, ou q, ou les deux", autrement dit, il est inclus. En anglais, le mot «ou» est parfois inclus (par exemple, "la crème ou de sucre?»), Mais il est parfois exclusive (par exemple, "café ou de thé?" Est généralement destiné à signifier un ou l'autre, pas les deux). De même, le mot anglais «certains» peut signifier «au moins un, peut-être tous", mais d'autres fois, cela peut signifier "pas tous, peut-être pas". Le mot anglais "et" doit parfois être traduit par "ou" (par exemple, "les hommes et les femmes peuvent se appliquer").
Limitations de la logique du premier ordre
Toutes les notations mathématiques ont leurs forces et leurs faiblesses;voici quelques ces questions avec la logique du premier ordre.
Difficulté représentant if-then-else
Curieusement, FOL avec l'égalité (comme généralement défini) ne comprend ni ne permet la définition d'un if-then-else prédicat ou une fonction si (c, a, b), où "c" est une condition exprimé en une formule, alors a et b sont soit les deux termes ou les deux formules, et son résultat serait "une" si c est vrai, et "b" si elle est fausse. Le problème est que dans FOL, deux prédicats et fonctions ne peuvent accepter les termes («non-booléens») en tant que paramètres, mais la représentation «évidente» de l'état est une formule ("booléen"). Cela est regrettable, car beaucoup de fonctions mathématiques sont commodément exprimées en termes de si-alors-sinon, et si-alors-sinon est fondamentale pour décrire la plupart des programmes informatiques.
Mathématiquement, il est possible de redéfinir un ensemble complet de nouvelles fonctions répondant aux opérateurs de la formule, mais cela est assez maladroite. Un prédicat si (c, a, b) peut être exprimée dans FOL se réécrit sous la forme  , mais cela est maladroite si la condition c est complexe. Beaucoup étendent FOL pour ajouter un prédicat cas spécial nommé "if (condition, a, b)" (où a et b sont des formules) et / ou de la fonction "ite (état, a, b)" (où a et b sont des termes ), qui tous deux accepter une formule comme la condition, et sont égaux à "a" si la condition est vraie et "b" si elle est fausse. Ces extensions font FOL plus facile à utiliser pour certains problèmes, et de faire certains types d'automatique théorème prouvant facile. D'autres l'étendent FOL davantage afin que les fonctions et prédicats peuvent accepter les deux termes et formules à toute position.
, mais cela est maladroite si la condition c est complexe. Beaucoup étendent FOL pour ajouter un prédicat cas spécial nommé "if (condition, a, b)" (où a et b sont des formules) et / ou de la fonction "ite (état, a, b)" (où a et b sont des termes ), qui tous deux accepter une formule comme la condition, et sont égaux à "a" si la condition est vraie et "b" si elle est fausse. Ces extensions font FOL plus facile à utiliser pour certains problèmes, et de faire certains types d'automatique théorème prouvant facile. D'autres l'étendent FOL davantage afin que les fonctions et prédicats peuvent accepter les deux termes et formules à toute position.
Typing (Sorts)
FOL ne comprend pas les types (sortes) dans la notation elle-même, autres que la différence entre les formules ("booléens") et des termes («non-booléens"). Certains affirment que ce manque de types est un grand avantage, mais beaucoup d'autres trouvent des avantages dans la définition et l'utilisation de types (sortes), comme aider les rejeter certaines spécifications erronées ou indésirables. Ceux qui souhaitent indiquer types doivent fournir ces informations en utilisant la notation disponible dans FOL. Cela peut faire de telles expressions plus complexes, et peut également être facile de se tromper.
Prédicats seul paramètre peuvent être utilisés pour mettre en œuvre la notion de types le cas échéant. Par exemple, dans: 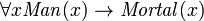 , le prédicat
, le prédicat 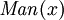 peut être considéré comme une sorte de "Type affirmation" (qui est, qui
peut être considéré comme une sorte de "Type affirmation" (qui est, qui 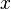 doit être un homme). Prédicats peut également être utilisé avec le "existe" quantifier pour identifier les types, mais cela devrait normalement être fait avec l'opérateur "et" à la place, par exemple:
doit être un homme). Prédicats peut également être utilisé avec le "existe" quantifier pour identifier les types, mais cela devrait normalement être fait avec l'opérateur "et" à la place, par exemple: 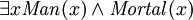 ("il existe quelque chose qui est à la fois un homme et est mortel"). Il est facile d'écrire
("il existe quelque chose qui est à la fois un homme et est mortel"). Il est facile d'écrire 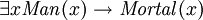 , mais ce serait équivalent à
, mais ce serait équivalent à 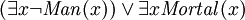 ("il ya quelque chose qui ne soit pas un homme, et / ou il existe quelque chose qui est mortel"), qui est généralement pas ce qui était prévu. De même, les affirmations peuvent être faites qu'un type est un sous-type d'un autre type, par exemple:
("il ya quelque chose qui ne soit pas un homme, et / ou il existe quelque chose qui est mortel"), qui est généralement pas ce qui était prévu. De même, les affirmations peuvent être faites qu'un type est un sous-type d'un autre type, par exemple: 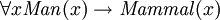 («pour tous
(«pour tous 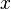 , si
, si 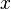 est un homme, alors
est un homme, alors 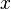 est un mammifère ").
est un mammifère ").
Difficulté à finitude caractériser ou responsabilisation
Il résulte de ce Löwenheim-Skolem qu'il ne soit pas possible de caractériser la finitude ou de responsabilisation dans la logique du premier ordre. Par exemple, dans la logique du premier ordre on ne peut pas affirmer la propriété moins-limite supérieure pour des ensembles de nombres réels , qui stipule que tout, non vide délimité des nombres réels a une borne supérieure; Un logique du deuxième ordre est nécessaire pour cela.
Graphique accessibilité ne peut être exprimée
Plusieurs situations peuvent être modélisés comme un graphe de noeuds et de connexions dirigées (bords). Par exemple, la validation de nombreux systèmes nécessite montrant qu'un «mauvais» état ne peut être atteint à partir d'un «bon» état, et ces interconnexions des Etats peut souvent être modélisé comme un graphe. Cependant, il peut être prouvé que la connectivité ne peut être pleinement exprimée dans la logique des prédicats. En d'autres termes, il n'y a pas de formule prédicat logique 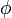 et
et 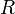 comme seul symbole de prédicat (d'arité 2) de telle sorte que
comme seul symbole de prédicat (d'arité 2) de telle sorte que 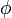 tient dans une interprétation
tient dans une interprétation 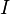 si et seulement si l'extension du
si et seulement si l'extension du 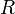 en
en 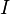 décrit un graphe connexe: qui est, graphes connexes ne peuvent pas être axiomatiser.
décrit un graphe connexe: qui est, graphes connexes ne peuvent pas être axiomatiser.
Notez que donnée une relation binaire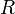 codant pour un graphe, on peut décrire
codant pour un graphe, on peut décrire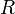 en termes d'une conjonction de formules du premier ordre, et d'écrire une formule
en termes d'une conjonction de formules du premier ordre, et d'écrire une formule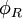 qui est satisfiable si et seulement si
qui est satisfiable si et seulement si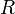 est connecté.
est connecté.
Comparaison avec d'autres logiques
- Logique du premier ordre typé permet variables et des termes d'avoir différents types (ou sortes ). Si il ya seulement un nombre fini de types, cela ne diffère pas vraiment grand-chose de logique du premier ordre, car on peut décrire les types avec un nombre fini de prédicats unaires et quelques axiomes. Parfois, il ya un type spécial de Ω valeurs de vérité, auquel cas les formules sont seulement termes de type Ω.
- Logique du premier ordre avec des conditions de domaine ajoute conditions de domaine (DC) à la logique du premier ordre classique, permettant la manipulation des fonctions partielles; ces conditions peuvent être prouvées "sur le côté" d'une manière similaire à des conditions de type exactitude de PVS. Il ajoute également si-alors-sinon de garder les définitions et les preuves gérables (ils sont devenus trop complexes sans eux).
- Le standard SMT-LIB définit un langage utilisé par de nombreux groupes de recherche pour les théories satisfiability modulo; la logique complète est basée sur FOL avec l'égalité, mais ajoute sortes (types), if-then-else pour les termes et formules (ITE () et si .. alors .. d'autre ..), un let construire pour les termes et formules ( laisser et flet), et un distincte construction déclarant un ensemble de valeurs cotées en tant que distincte. Ses connecteurs sont pas , implique , et , ou , xor , et ssi .
- Logique du deuxième ordre Faiblepermet la quantification sur des sous-ensembles finis.
- Logique du second ordre monadiquepermet la quantification sur des sous-ensembles, ou en d'autres termes plusunaireprédicats.
- Logique du deuxième ordre permet la quantification sur des sous-ensembles et des relations, ou en d'autres termes plus de tous les prédicats. Par exemple, le axiome de extensionnalité peut être indiqué dans la logique du deuxième ordre que x = y ≡ def
 P ( P ( x ) ↔ P ( y )). Les fortes sémantique de la logique du second ordre donnent ces phrases un sens beaucoup plus forte que la sémantique de premier ordre.
P ( P ( x ) ↔ P ( y )). Les fortes sémantique de la logique du second ordre donnent ces phrases un sens beaucoup plus forte que la sémantique de premier ordre. - Ordre supérieur logiques permet la quantification sur les types plus élevés que de second ordre logiques permis. Ces types supérieurs comprennent les relations entre les relations, les fonctions de relations aux relations entre les relations, etc.
- Logique du premier ordre Intuitionistic utilise intuitionniste plutôt que le calcul propositionnel classique; par exemple, ¬¬φ ne doit pas être équivalente à φ. De même, logique floue de premier ordre sont des extensions de premier ordre de la logique floue propositionnelles plutôt que la logique classique.
- La logique modalea supplémentairesopérateurs modauxavec des significations qui peuvent être caractérisés de façon informelle, par exemple "il est nécessaire que φ" et "il est possible que φ".
- En prédicat monadique calculdes prédicats sont limités à avoir un seul argument.
- Logique infinitaire permet infiniment longues peines. Par exemple, on peut permettre une conjonction ou de disjonction d'une infinité de formules, ou quantification infiniment plus grand nombre de variables. Infiniment longues peines se posent dans les domaines des mathématiques, y compris la topologie et théorie des modèles.
- Logique du premier ordre avec des quantificateurs supplémentairesa de nouveaux quantificateursQx, ..., avec des significations telles que "il ya beaucoup dextelle que ... ". Voir aussi quantificateurs de branchement et lesquantificateurs pluriel deGeorge Boolos et d'autres.
- La logique des prédicats des définitions (PLD, ou D-logique) modifie FOL en ajoutant formellement définitions syntaxiques comme un type de valeur (en plus de formules et modalités); ces définitions peuvent être utilisés à l'intérieur des termes et formules.
- logique de l'Indépendance de l'environnementest caractérisé pardes quantificateurs de branchement, qui permettent d'exprimer indépendance entre variables quantifiées.
La plupart de ces logiques sont dans certaines extensions de sens de FOL: ils comprennent tous les quantificateurs et des opérateurs logiques de FOL avec les mêmes significations. Lindström a montré que FOL a pas d'extensions (autres qu'elle-même) qui satisfont à la fois le théorème de compacité et de la baisse théorème Löwenheim-Skolem. Une déclaration précise de théorème de Lindström nécessite quelques conditions techniques que la logique est supposé satisfaire; par exemple, en changeant les symboles d'une langue ne devrait faire aucune différence essentielle à laquelle phrases sont vraies.
Algebraizations
Trois moyens d'éliminer les variables quantifiées de FOL, et qui ne comportent pas de remplacer les quantificateurs avec d'autres opérateurs de liaison variables terme, sont connus:
- Algèbre cylindrique, parAlfred Tarski et ses collègues;
- Algèbre polyadique, parPaul Halmos;
- Logique de foncteur prédicat, principalement en raison deWillard Quine.
Cesalgèbres:
- Sont toutes les extensions propres de l'deux éléments algèbre de Boole, et sont doncréseaux;
- Faire pour FOL ceLindenbaum-Tarski algèbre fait pourla logique propositionnelle;
- Autoriser les résultats del'algèbre abstraite,algèbre universelle, etla théorie de l'ordre à être exercées sur FOL.
Tarski et Givant (1987) montrent que le fragment de FOL qui n'a pas de phrase atomique se trouvant dans le champ d'application de plus de trois quantificateurs, a le même pouvoir expressif que rapport algèbre. ce fragment est d'un grand intérêt, car il suffit à l'arithmétique de Peano et plus la théorie des ensembles axiomatique , y compris le canonique ZFC. Ils prouvent aussi que FOL avec une primitive paire ordonnée est équivalent à une algèbre de relation avec deux paires commandées fonctions de projection.
Automatisation
Théorèmes de logique du premier ordre est l'un des sous-champs plus matures de démonstration automatique. La logique est suffisamment expressif pour permettre la spécification de problèmes arbitraires, souvent d'une manière raisonnablement naturelle et intuitive. D'autre part, il est encore semidecidable, et un certain nombre de sons et complètes calculs ont été développés, permettant systèmes entièrement automatisés. En 1965, J. Alan Robinson a réalisé une percée importante avec son approche de la résolution; pour prouver un théorème il tente de réfuter le théorème niée, d'une manière orientée vers un but, résultant dans une méthode beaucoup plus efficace pour prouver des théorèmes automatiquement dans FOL. Plus logiques expressives, comme d'ordre supérieur et de la logique modale, permettent l'expression pratique d'un large éventail de problèmes que la logique du premier ordre, mais théorèmes pour ces logiques est moins bien développés.
Une nouvelle technologie moderne et particulièrement perturbateur est que dessolveurs SMT, qui ajoutent l'arithmétique et le soutien des propositions pour les classes de puissantssolveurs SAT.