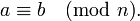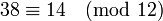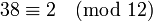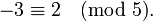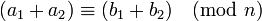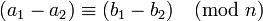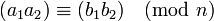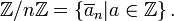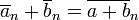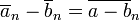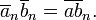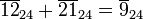Arithmétique modulaire

À propos de ce écoles sélection Wikipedia

Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?

Arithmétique modulaire (parfois appelé modulo arithmétique, l'arithmétique ou l'horloge) est un système de calcul pour les entiers , là où le nombre "enveloppent" après avoir atteint une certaine valeur - le module. Arithmétique modulaire a été introduit par Carl Friedrich Gauss dans son livre Disquisitiones Arithmeticae, publié en 1801.

Un usage familier de l'arithmétique modulaire est son utilisation dans le 24 heures: l'arithmétique des garde-temps dans lequel le jour va de minuit à minuit et est divisé en 24 heures, numérotés de 0 à 23. Si le temps est maintenant 19h00 - 07 heures dans la soirée - puis huit heures plus tard, il sera 3h00. Outre habitude suggère que le temps plus tard, devrait être 19 + 8 = 27, mais ce ne est pas la réponse parce que le temps de l'horloge "se enroule autour de" à la fin de la journée. De même, si l'horloge commence à 12h00 (midi) et 21 heures se écouler, puis le temps sera 9h00 le lendemain, plutôt que de 33:00. Comme le nombre de heures recommence quand il atteint 24, ce est l'arithmétique modulo 24. Il est à noter que dans ce système ne est pas un 24:00 heure valide parce que ce est égale au 0:00 du jour suivant, de la même manière 2:60 heure ne est pas valable, car il est égal à 3: 00.

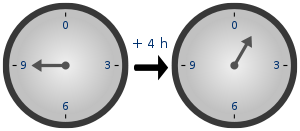
Chronométrage sur une horloge donne un exemple de l'arithmétique modulaire.

La relation de congruence

Arithmétique modulaire peut être manipulé mathématiquement par l'introduction d'un relation de congruence sur les nombres entiers qui est compatible avec les opérations de la anneau des entiers: outre , la soustraction et la multiplication . Pour un module fixe n, elle est définie comme suit.

Deux entiers a et b sont dits être congruents modulo n, si leur différence a - b est un nombre entier multiple de n. Si tel est le cas, elle est exprimée en tant que:

$un \ equiv b \ pmod n. \,$

L'énoncé mathématique ci-dessus est lu: «un est congru à b modulo n".

Par exemple,

$38 \ equiv 14 \ pmod {12} \,$

parce 38-14 = 24, qui est un multiple de 12. Pour n positive et une non-négatif et b, la congruence de A et B peut également être considéré comme affirmant que ces deux nombres ont la même reste de la division par le module n. Alors,

$38 \ 2 equiv \ pmod {12} \,$

parce que, quand divisé par 12, les deux chiffres donnent 2 comme reste.

La même règle se applique pour les valeurs négatives d'un:

$-3 \ Equiv 2 \ pmod 5. \,$

Une remarque sur la notation: Parce qu'il est d'usage de considérer plusieurs relations de congruence pour les différents modules en même temps, le module est intégré dans la notation. En dépit de la notation ternaire, la relation de congruence pour un module donné est binaire. Cela aurait été plus clair si la notation a ≡ _n b avait été utilisé, au lieu de la notation traditionnelle commune.

Les propriétés qui rendent cette relation une relation de congruence (respectent addition, la soustraction et la multiplication) sont les suivantes.

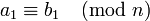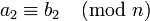Si $a_1 \ equiv b_1 \ n pmod$ et $a_2 \ equiv b_2 \ n pmod$ , Puis:

$(A_1 + a_2) \ equiv (b_1 + b_2) \ pmod n \,$
$(A_1 - a_2) \ equiv (b_1 - b_2) \ pmod n \,$
$(A_1 a_2) \ equiv (b_1 b_2) \ pmod n \,$

L'anneau des classes de congruence

Comme toute relation de congruence, la congruence modulo n est un relation d'équivalence , et de la classe d'équivalence de l'entier a, notée 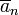$\ Overline {a} _n$ , Est l'ensemble 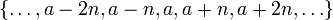$\ \ Gauche {\ ldots, a - 2n, a - n, A, A + n, a + 2n, \ ldots \ right \}$ . Cet ensemble, composé des entiers congruents à un modulo n, est appelée la classe de congruence ou une catégorie d'résidu d'un modulo n. Un autre notation pour cette classe de congruence, qui exige que dans le cadre du module est connu, est $\ Displaystyle [a]$ .

L'ensemble des classes de congruence modulo n est notée 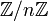$\ Mathbb {Z} / n \ mathbb {Z}$ et définie par:

$\ Mathbb {Z} / n \ mathbb {Z} = \ \ left {\ overline {a} _n | a \ in \ mathbb {Z} \ right \}.$

Lorsque n ≠ 0, 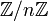$\ Mathbb {Z} / n \ mathbb {Z}$ a n éléments, et peut être écrite comme:

$\ Mathbb {Z} / n \ mathbb {Z} = \ \ left {\ overline {0} _n, \ overline {1} _n, \ overline {2} _n, \ ldots, \ overline {n-1} _n \ right \}.$

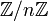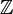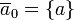Lorsque n = 0, $\ Mathbb {Z} / n \ mathbb {Z}$ ne pas avoir zéro éléments; il se agit plutôt isomorphe à $\ Mathbb {Z}$ Car $\ Overline {a} _0 = \ \ left {a \ right \}$ .

Nous pouvons définir addition, soustraction, multiplication et sur 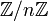$\ Mathbb {Z} / n \ mathbb {Z}$ par les règles suivantes:

$\ Overline {a} _n + \ overline {b} _n = \ overline {a + b} _n$
$\ Overline {a} _n - \ overline {b} _n = \ overline {a - b} _n$
$\ Overline {a} _n \ overline {b} _n = \ overline {ab} _n.$

La vérification que ce est une bonne définition utilise les propriétés indiquées auparavant.

De cette façon, 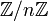$\ Mathbb {Z} / n \ mathbb {Z}$ devient un anneau commutatif . Par exemple, dans le cycle 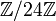$\ Mathbb {Z} / 24 \ mathbb {Z}$ , Nous avons

$\ Overline {12} _ {24} + \ overline {21} _ {24} = \ overline {9} _ {24}$

comme dans l'arithmétique pour l'horloge de 24 heures.

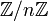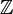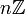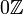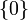La notation $\ Mathbb {Z} / n \ mathbb {Z}$ est utilisé, car il est le anneau de facteur $\ Mathbb {Z}$ par le idéal $n \ mathbb {Z}$ contenant tous les entiers divisible par n, où $0 \ mathbb {Z}$ est le singleton ensemble $\ \ Left {0 \ right \}$ .

En termes de groupes, la classe de résidus 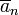$\ Overline {a} _n$ est le un ensemble complémentaire de l'en groupe quotient 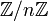$\ Mathbb {Z} / n \ mathbb {Z}$ , Un groupe cyclique .

L'ensemble 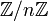$\ Mathbb {Z} / n \ mathbb {Z}$ a un certain nombre de propriétés mathématiques importants qui sont fondamentales pour diverses branches des mathématiques.

Plutôt que d'exclure le cas particulier n = 0, il est plus utile d'inclure 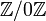$\ Mathbb {Z} / 0 \ mathbb {Z}$ (Qui, comme mentionné précédemment, est isomorphe à l'anneau 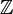$\ Mathbb {Z}$ des nombres entiers), par exemple lors de l'examen de la caractéristique d'un anneau.

Restes

La notion de l'arithmétique modulaire est liée à celle de la reste dans la division . Le fonctionnement de trouver le reste est parfois appelé le Modulo et nous pourrions voir "2 = 14 (mod 12)". La différence réside dans l'utilisation de la congruence, indiqué par ≡, et l'égalité indiquer par =. L'égalité implique spécifiquement le «résidu commun», le membre le moins non-négatif d'une classe d'équivalence. Lorsque vous travaillez avec l'arithmétique modulaire, chaque classe d'équivalence est généralement représenté par son résidu commune, par exemple "38 ≡ 2 (mod 12)" qui peut être trouvé en utilisant division longue. Il se ensuit que, se il est exact de dire «38 ≡ 14 (mod 12)", "2 ≡ 14 (mod 12)» et «2 ≡ 14 (mod 12)", il est inexact de dire "38 = 14 ( mod 12) "(avec" = "plutôt que" ≡ ").

Les parenthèses sont parfois retirés de l'expression, par exemple "38 ≡ 14 mod 12" ou "2 = 14 mod 12", ou placés autour du diviseur par exemple "38 ≡ 14 mod (12)". Notation comme "38 (mod 12)" a également été observée, mais est ambigu sans clarification contextuelle.

La relation de congruence est parfois exprimé en utilisant au lieu de modulo mod, comme "38 ≡ 14 (modulo 12)" dans l'informatique . La fonction modulo dans différents langages informatiques donné généralement le résidu commun, par exemple la mention «y = MOD (38,12);" donne y = 2.

Applications

Arithmétique modulaire est référencé dans la théorie des nombres , la théorie des groupes , la théorie des anneaux, la théorie des nœuds , l'algèbre abstraite , la cryptographie , l'informatique , la chimie et les visuels et musicaux arts.

Il est l'un des fondements de la théorie des nombres, touchant presque tous les aspects de son étude, et fournit des exemples clés de la théorie des groupes, théorie des anneaux et algèbre abstraite.

En cryptographie, l'arithmétique modulaire sous-tend directement systèmes clés publiques telles que RSA et Diffie-Hellman, ainsi que de fournir corps finis qui sous-tendent les courbes elliptiques , et est utilisé dans une variété de y compris des algorithmes à clé symétrique AES, IDEA, et RC4.

En informatique, l'arithmétique modulaire est souvent appliquée opérations bit à bit et autres opérations impliquant de largeur fixe, cyclique structures de données. Le Modulo, telle que transposée dans de nombreux langages de programmation et les calculatrices , est une application de l'arithmétique modulaire qui est souvent utilisé dans ce contexte.

En chimie, le dernier chiffre de la Numéro de registre CAS (un nombre qui est unique pour chaque composé chimique) est un chiffre de contrôle, qui est calculé en prenant le dernier chiffre des deux premières parties de la Numéro de registre CAS une fois, les temps de chiffres suivante 2, les temps de chiffres suivante 3 etc., en ajoutant tous ces et calculer la somme modulo 10.

Dans les arts visuels, l'arithmétique modulaire peut être utilisé pour créer des motifs artistiques basées sur les tables de multiplication et d'addition modulo n (voir lien externe, ci-dessous).

En musique, l'arithmétique modulo 12 est utilisé dans l'examen du système de dodécaphonique tempérament égal, où Octave et enharmoniques équivalence se produit (ce est-emplacements dans un rapport 01:02 ou 02:01 sont équivalents, et C- Sharp est considérée comme identique à D- plat).

Procédé selon la Preuve par neuf offre une vérification rapide de calculs arithmétiques décimales réalisées à la main. Il est basé sur l'arithmétique modulaire modulo 9, et plus particulièrement sur la propriété crucial que 10 ≡ 1 (mod 9).

Plus généralement, l'arithmétique modulaire a également une application dans des disciplines telles que le droit (voir, par exemple, répartition), l'économie , (voir, par exemple, la théorie des jeux ) et d'autres domaines de la sciences sociales, où répartition proportionnelle et l'allocation des ressources joue un rôle central de l'analyse.

Certains neurologues (voir, par exemple, Oliver Sacks) théoriser que ce qu'on appelle savants autistes utilisent une arithmétique modulaire «innée» pour calculer ces problèmes complexes que ce jour de la semaine d'une date lointaine va tomber sur.

Complexité de calcul

Depuis arithmétique modulaire a une telle large gamme d'applications, il est important de savoir comment il est difficile de résoudre un système d'congruences. Un système de congruences linéaire peut être résolu en temps polynomial avec une forme d' élimination de Gauss , pour plus de détails voir le linéaire théorème de congruence.

Résoudre un système d'équations non-linéaires arithmétiques modulaire est NP-complet. Pour plus de détails, voir par exemple M. Garey, DS Johnson: Ordinateurs et intraitable, un Guide de la théorie de la NP-complétude, WH Freeman 1979.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Modular_arithmetic&oldid=199402396 "