Groupe cyclique

Dans la théorie des groupes , un groupe cyclique ou un groupe monogène est un groupe qui peut être générée par un élément unique, en ce sens que le groupe comporte un élément g (appelé " générateur "du groupe) de telle sorte que, lors de l'écriture par multiplication, chaque élément du groupe est une puissance de g (un multiple de g lorsque la notation est additif).

Définition

Un groupe cyclique G est appelé se il existe un élément g de G tel que G = <g> g = ^{n | ⁿ est un nombre entier}. Depuis ne importe quel groupe générée par un élément dans un groupe est un sous-groupe de ce groupe, montrant que la seule sous-groupe de G de groupe qui contient g G est elle-même suffit à montrer que G est cyclique.

Par exemple, si G = {g ^0, g ^1, g ^2, g ^3, g ^4, g ^5} est un groupe, puis ⁶ g = g ^0, et G est cyclique. En fait, G est essentiellement la même que (ce est- isomorphe à) l'ensemble {0, 1, 2, 3, 4, 5} avec addition modulo 6. Par exemple, 1 + 2 = 3 (mod 6) correspond à ¹ g ² g · g = ^3, et 2 + 5 = 1 (mod 6) correspond à ² g · g ⁵ = g = g ^{1 7,} et ainsi de suite . On peut utiliser l'isomorphisme φ définie par φ (g ⁱ⁾ = i.

Pour tout entier positif n il ya exactement un groupe cyclique (à isomorphisme près) dont l'ordre est n, et il ya exactement un groupe cyclique infini (les entiers de moins de plus). Ainsi, les groupes cycliques sont les groupes les plus simples et ils sont totalement classés.

Le nom «cyclique» peut être trompeuse: il est possible de générer un nombre infini d'éléments et non former des cycles littérales; ce est, tous les 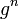est distincte. (On peut dire qu'il a une infiniment long cycle.) Un groupe généré de cette manière est appelé un groupe cyclique infini, et est isomorphe au groupe additif des nombres entiers Z.

Étant donné que les groupes cycliques sont abélien, ils sont souvent écrits additive et notés Z _n. Toutefois, cette notation peut être problématique pour les théoriciens des nombres , car il entre en conflit avec la notation habituelle pour p nombre -adique anneaux ou localisation à un idéal premier. Le notations quotient Z / n Z, Z / n, et Z / (n) sont des solutions standard. Nous adoptons la première de ces ici pour éviter la collision de la notation. Voir aussi la section sous-groupes et la notation ci-dessous.

On peut écrire le groupe multiplicativement, et notons par C _n, où n est l'ordre (qui peut être ∞). Par exemple, g ³ g ⁴ g = ² à C _5, alors que 3 + 4 = 2 dans Z / Z 5.

Propriétés

Le théorème fondamental de groupes cycliques stipule que si G est un groupe cyclique d'ordre n puis tous sous-groupe de G est cyclique. En outre, l'ordonnance d'un sous-groupe de G est un diviseur de n et pour chaque diviseur positif k de n le groupe G a exactement un sous-groupe d'ordre k. Cette propriété caractérise groupes cycliques finis: un groupe d'ordre n est cyclique si et seulement si pour tout diviseur d de n le groupe possède au plus un sous-groupe d'ordre d. Parfois, la déclaration équivalente est utilisée: un groupe d'ordre n est cyclique si et seulement si pour tout diviseur d de n le groupe a exactement un sous-groupe d'ordre d.

Chaque groupe cyclique fini est isomorphe au groupe {[0], [1], ..., [n - 1]} des entiers modulo n, par addition, et tout groupe cyclique infini est isomorphe à Z (l'ensemble de tous les entiers) sous addition. Ainsi, il suffit de regarder ces groupes à comprendre les propriétés de groupes cycliques en général. Ainsi, des groupes cycliques sont l'un des groupes les plus simples à étudier et à un certain nombre de propriétés intéressantes sont connus.

Étant donné un groupe cyclique G d'ordre n (n peut être infini) et pour tout g dans G,

• G est abélien; ce est, leur opération de groupe est commutatif: gh = hg (pour tout h dans G). Il en est ainsi depuis g + h mod n = h + g mod n.
• Si n est fini, alors g = g ^{n 0} est un élément du groupe de l'identité, puisque n = 0 mod n.
• Si n = ∞, alors il ya exactement deux générateurs: à savoir 1 et -1 pour Z, et tous les autres mappés à eux sous un isomorphisme dans d'autres groupes cycliques infinis.
• Si n est fini, alors il ya exactement φ (n) générateurs où φ est le Fonction de phi d'Euler
• Chaque sous-groupe de G est cyclique. En effet, chaque sous-groupe fini de G est un groupe de {0, 1, 2, 3, ..., m - 1} avec addition modulo m. Et chaque sous-groupe infini de G est m Z pour un m, qui est bijective à (donc isomorphe à) Z.
• G _n est isomorphe à Z / n Z ( groupe de facteurs de Z sur Z n) depuis Z / n Z = {0 + Z n, Z n + 1, n + 2 Z, Z n + 3, 4 + Z n, ..., n - 1 + n Z } 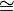{0, 1, 2, 3, 4, ..., n - 1} pour l'addition modulo n.

Plus généralement, si d est un diviseur de n, alors le nombre d'éléments dans Z / n qui ont ordre d est φ (d). L'ordre de la classe de résidus de m est n / pgcd (n, m).

Si p est un nombre premier , alors le seul groupe ( jusqu'à isomorphisme) à p éléments est le groupe cyclique C ou Z _p / p Z.

Le produit direct de deux groupes cycliques Z / n Z et Z / Z m est cyclique si et seulement si n et m sont premiers entre eux. Ainsi par exemple, Z / Z 12 est le produit direct de Z / Z et Z 3 / Z 4, mais pas le produit direct de Z / 6 Z et Z / Z 2.

La définition implique immédiatement que les groupes cycliques ont très simple présentation du groupe C = _∞ <x |> et C _n = <x | x ^n> pour n fini.

Un groupe cyclique primaire est un groupe de la forme Z / p ^k où p est un nombre premier . Le théorème fondamental de groupes abéliens stipule que chaque groupe abélien de type fini est le produit direct d'un nombre fini groupes cycliques cycliques et infinis primaires finis.

Z / n Z et Z sont également anneaux commutatifs . Si p est premier, alors Z / p Z est un corps fini, également désigné par F _p ou GF (p). Chaque champ à p éléments est isomorphe à celui-ci.

Le unités de l'anneau Z / n Z sont les numéros premier avec n. Ils forment un groupe sous la multiplication modulo n avec φ (n) éléments (voir ci-dessus). Il est écrit que (Z / n Z) ^×. Par exemple, nous obtenons (Z / n Z) ^× = {1,5} lorsque n = 6, et obtenir des (Z / n Z) ^× = {1,3,5,7} lorsque n = 8.

En fait, on sait que (Z / Z n) ^× est cyclique si et seulement si n est égal à 2 ou 4 ou 2 ou p ^k p ^k pour un impaire nombre premier p et k ≥ 1, dans ce cas, tous les générateurs de (Z / n Z) ^× est appelé primitive modulo n racine. Ainsi, (Z / Z n) ^× est cyclique pour n = 6, mais pas pour n = 8, où il est isomorphe à la place Groupe de Klein.

Le groupe (Z / p Z) ^× est cyclique avec p - 1 éléments pour chaque nombre premier p, et est aussi écrit (Z / p Z) ^* parce qu'il se compose des éléments non nuls. Plus généralement, tous les finis sous-groupe du groupe multiplicatif de toute champ est cyclique.

Exemples

En 2D et 3D de la groupe de symétrie pour n -fois symétrie de rotation est C _n, d'un groupe type abstrait Z _n. En 3D, il ya également d'autres groupes de symétrie qui sont algébriquement même, voir Groupes de symétrie cyclique en 3D.

Notez que le groupe S ¹ de toutes les rotations d'un cercle (le Groupe de cercle) ne est pas cyclique, car il ne est même pas dénombrable.

La ^n-ième racines de l'unité forment un groupe cyclique d'ordre n pour la multiplication. par exemple, 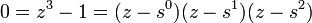où 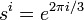et un groupe de 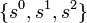la multiplication est cyclique.

Le De chaque groupe de Galois fini l'extension du champ d'un champ fini est fini et cyclique; à l'inverse, étant donné un corps fini F et un groupe cyclique fini G, il est une extension finie de F dont le groupe de Galois G est sur le terrain.

Représentation

Le graphiques du cycle de groupes cycliques finis sont tous les polygones n -sided avec les éléments aux sommets. Le sommet sombre dans les graphiques ci-dessous de cycle pour tenir l'élément d'identité et les autres sommets sont les autres éléments du groupe. Un cycle est constitué de puissances successives de l'un des éléments connectés à l'élément d'identité.

C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8

Le la théorie de la représentation du groupe cyclique est un cas de base essentiel pour la théorie des représentations des groupes finis plus générales. Dans le affaire complexe, une représentation d'un groupe cyclique se décompose en une somme directe de caractères linéaires, faisant le lien entre la théorie des caractères et la théorie de la représentation transparente. Dans le cas caractéristique positive, les représentations indécomposables du groupe cyclique former un modèle et une base inductive pour la théorie de la représentation des groupes avec cyclique Sous-groupes de Sylow et plus généralement la théorie de la représentation des blocs de défaut cyclique.

Sous-groupes et la notation

Tous et des sous-groupes groupes quotients de groupes cycliques sont cycliques. Plus précisément, tous les sous-groupes de Z sont de la forme m Z, avec un nombre entier m ≥0. Tous ces sous-groupes sont différents, et à part le groupe trivial (pour m = 0) sont tous isomorphe à Z. Le réseau de sous-groupes de Z est isomorphe au double du réseau des nombres naturels ordonnées par la divisibilité . Tous les groupes de facteurs de Z sont limitées, sauf pour l'exception trivial Z / {0} = Z / 0 Z. Pour chaque diviseur D positif de n, le groupe quotient Z / Z n a une précision sous-groupe d'ordre d, l'une générée par la classe de résidus de n / d. Il n'y a pas d'autres sous-groupes. Le réseau de sous-groupes est donc isomorphe à l'ensemble des diviseurs de n, ordonnée par la divisibilité. En particulier, un groupe cyclique est simple si et seulement si son ordre (le nombre de ses éléments) est premier.

Utilisation du groupe quotient formalisme, Z / n Z est une notation standard pour le groupe cyclique additif à n éléments. En terminologie annulaire, le sous-groupe Z n est la idéal (n), de sorte que le quotient peut également être écrit Z / (n) ou Z / n sans abus de notation. Ces solutions de rechange ne sont pas incompatibles avec la notation pour les p entiers -adiques. La dernière forme présente l'avantage supplémentaire qu'il lit de la même façon que le groupe ou l'anneau est souvent décrit verbalement, «Zee mod en".

Comme un problème pratique, on peut être donné un sous-groupe fini d'ordre n C, générée par un élément g, et a demandé de trouver la taille m du sous-groupe engendré par G ^k pour un certain entier k. Ici m sera le plus petit entier> 0 tel que mk est divisible par n. Il est donc n / m où m = (k, n) est la pgcd de k et n. En d'autres termes, la indice du sous-groupe engendré par g ^k est m. Ce raisonnement est connu comme le algorithme de calcul de l'indice, dans la théorie des nombres .

Endomorphismes

Le anneau commutatif endomorphisme du groupe Z / n Z est isomorphe à Z / n Z lui-même en tant que anneau. Sous cet isomorphisme, le nombre r correspond à la endomorphisme de Z / n Z qui mappe chaque élément à la somme de r copies de celui-ci. Ce est une bijection si et seulement si r est premier avec n, de sorte que le groupe automorphisme de Z / n Z est isomorphe au groupe de base (Z / n Z) ^× (voir ci-dessus).

De même, l'anneau des endomorphismes du groupe additif Z est isomorphe à l'anneau Z. Son groupe d'automorphismes est isomorphe au groupe d'unités de l'anneau Z, ce est-à {-1, 1} 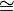C _2.

Pratiquement groupes cycliques

Un groupe est appelé pratiquement cyclique si elle contient un sous-groupe cyclique fini de index. Il est connu qu'un type fini groupe discret avec exactement deux extrémités est pratiquement cyclique. Chaque sous-groupe abélien d'un Groupe hyperbolique Gromov est pratiquement cyclique.