Statistiques

Un graphique d'une courbe normale montrant statistiques utilisées dans évaluation des tests standardisés. Les échelles comprennent les écarts-types , les pourcentages cumulatifs, équivalents centiles, Z-scores, T-score, neufs, standards et pourcentages nines standard.

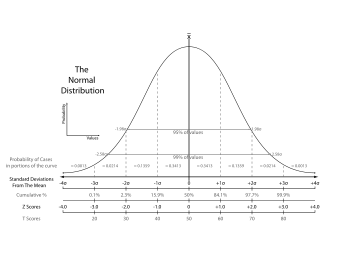
Statistique est une science mathématique relative à la collecte, l'analyse, l'interprétation ou explication, et la présentation des données. Elle est applicable à une grande variété de disciplines universitaires, des naturelles et sociales sciences aux sciences humaines et aux gouvernement et les entreprises.

Des méthodes statistiques peuvent être utilisées pour résumer ou décrire une collecte de données; cela se appelle statistiques descriptives. En outre, les modèles dans les données peuvent être modélisé d'une manière qui tient compte de le hasard et l'incertitude dans les observations, et ensuite utilisé pour tirer des conclusions sur le processus ou de la population à l'étude; cela se appelle inférence statistique. Les deux statistiques descriptives et inférentielles comprennent statistiques appliquées. Il ya aussi une discipline appelée statistiques mathématiques, qui sont concernés par la base théorique du sujet.

Les statistiques de mot est aussi le pluriel de statistique (au singulier), qui fait référence au résultat de l'application d'un algorithme statistique pour un ensemble de données, comme dans statistiques économiques, statistiques de la criminalité, etc.

Histoire

Statistiques surgi, au plus tard le 18ème siècle , de la nécessité des États à recueillir des données sur leurs populations et les économies, afin de les administrer. Son sens élargi au début du 19ème siècle pour inclure la collecte et l'analyse des données en général. statistiques est aujourd'hui largement utilisés dans le gouvernement, les entreprises et les sciences naturelles et sociales.

En raison de ses origines au sein du gouvernement et sa vue centrée sur les données monde, les statistiques sont considérées comme ne étant pas un sous-champ des mathématiques, mais plutôt un champ distinct qui utilise les mathématiques. Ses fondations mathématiques ont été portées dans les 17e et 18e siècles avec le développement de la théorie des probabilités . La méthode des moindres carrés , une technique central de la discipline, a été inventé dans le début du 19e siècle par plusieurs auteurs. Depuis lors de nouvelles techniques de probabilité et statistiques ont été en développement continu. Modernes ordinateurs ont accéléré à grande échelle d'un calcul statistique, et ont également rendu possible de nouvelles méthodes qui seraient impossible à effectuer manuellement.

Vue d'ensemble

En application des statistiques à un problème scientifique, industriel, ou sociétal, on commence par un processus ou population à étudier. Cela pourrait être une population de personnes dans un pays, de grains cristallins dans une roche ou de produits fabriqués par une usine particulière au cours d'une période donnée. Elle peut au contraire être un processus observé à plusieurs reprises; les données collectées sur ce genre de «population» constituent ce qu'on appelle un série chronologique.

Pour des raisons pratiques, plutôt que de la compilation des données sur toute une population, on étudie généralement un sous-ensemble de la population choisie, appelé un échantillon . Les données sont recueillies à propos de l'échantillon dans un ou observationnelle cadre expérimental. Les données sont ensuite soumis à une analyse statistique, qui sert deux objectifs connexes: description et inférence.

• Les statistiques descriptives peuvent être utilisés pour résumer les données, soit numérique ou graphique, pour décrire l'échantillon. Exemples de base de descripteurs numériques comprennent la moyenne et l'écart type . Récapitulations graphiques comprennent divers types de diagrammes et de graphiques.
• Les statistiques déductives est utilisé pour modéliser les modèles dans les données, ce qui représente hasard et de tirer des conclusions sur la population en général. Ces déductions peuvent prendre la forme de réponses aux questions oui / non ( tests d'hypothèses), les estimations des caractéristiques numériques ( estimation), les descriptions de l'association ( corrélation ), ou la modélisation des relations ( régression ). Autre techniques de modélisation comprennent ANOVA, les séries chronologiques, et l'exploration de données.

Le concept de corrélation est particulièrement remarquable. L'analyse statistique d'un ensemble de données peut révéler que deux variables (ce est deux propriétés de la population à l'étude) ont tendance à varier ensemble, comme se ils sont connectés. Par exemple, une étude du revenu annuel et l'âge de décès chez les personnes pourraient trouver que les pauvres ont tendance à avoir une vie plus courte que les personnes riches. Les deux variables sont dits être corrélées. Cependant, on ne peut pas déduire immédiatement l'existence d'une relation causale entre les deux variables (voir Corrélation ne implique pas causalité). Les phénomènes corrélée pourrait être causée par un troisième phénomène, jusqu'alors négligées, appelé tapi variable.

Si l'échantillon est représentatif de la population, alors les conclusions et les conclusions de l'échantillon peuvent être étendues à la population dans son ensemble. Un problème majeur réside dans la détermination de la mesure dans laquelle l'échantillon choisi est représentatif. Statistiques propose des méthodes pour estimer et corriger pour aléatoire dans l'échantillon et dans la procédure de collecte des données, ainsi que des méthodes pour concevoir des expériences solides en premier lieu (voir conception expérimentale).

Le concept mathématique fondamentale utilisée dans la compréhension de tels aléatoire est la probabilité . Statistique mathématique (aussi appelés théorie statistique) est la branche de mathématiques appliquées qui utilise la théorie et de probabilité analyse pour examiner la base théorique des statistiques.

L'utilisation de toute méthode statistique ne est valable que lorsque le système ou de la population à l'étude satisfait les hypothèses mathématiques de base de la méthode. Utilisation abusive des statistiques peut produire des erreurs subtiles mais graves dans la description et l'interprétation - subtile que même les professionnels expérimentés font parfois de telles erreurs et graves qu'ils peuvent influer sur la politique sociale, la pratique médicale et la fiabilité des structures comme les ponts et les centrales nucléaires. Même lorsque les statistiques est correctement appliquée, les résultats peuvent être difficiles à interpréter pour un non-expert. Par exemple, le signification statistique d'une tendance dans les données - qui mesure la mesure dans laquelle la tendance pourrait être causée par une variation aléatoire dans l'échantillon - peut ne pas être d'accord avec son sens intuitif de son importance. L'ensemble des compétences de base (statistiques) et le scepticisme nécessaires par des personnes à traiter des informations dans leur vie quotidienne est appelée littératie statistique.

Méthodes statistiques

Des études expérimentales et d'observation

Un objectif commun pour un projet de recherche statistique est d'étudier causalité, et en particulier de tirer une conclusion sur l'effet des changements dans les valeurs de prédicteurs ou variables indépendantes sur la réponse ou variables dépendantes. Il existe deux grands types d'études statistiques causales, des études expérimentales et des études d'observation. Dans les deux types d'études, l'effet des différences d'une variable indépendante (ou variables) sur le comportement de la variable dépendante sont observées. La différence entre les deux types est la façon dont l'étude est effectivement réalisée. Chacun peut être très efficace.

Une étude expérimentale consiste à prendre des mesures du système à l'étude, manipuler le système, puis prendre des mesures supplémentaires en utilisant la même procédure pour déterminer si la manipulation peut avoir modifié les valeurs des mesures. En revanche, une étude d'observation ne implique pas la manipulation expérimentale. Au lieu de cela les données sont recueillies et les corrélations entre les prédicteurs et la réponse sont étudiées.

Un exemple d'une étude expérimentale est la célèbre Hawthorne études qui ont tenté de tester les modifications à l'environnement de travail à l'usine de Hawthorne de la Western Electric Company. Les chercheurs se sont intéressés à savoir si l'éclairage accrue augmenterait la productivité de la travailleurs de première ligne d'assemblage. Les chercheurs ont d'abord mesuré la productivité dans l'usine alors modifiées l'éclairage dans une zone de l'usine pour voir si des changements dans l'éclairage seraient affecter la productivité. Comme il se avère, la productivité améliorée dans toutes les conditions expérimentales (voir Effet Hawthorne). Cependant, l'étude est aujourd'hui fortement critiqué pour des erreurs dans les procédures expérimentales, en particulier l'absence d'une groupe témoin et blindedness .

Un exemple d'une étude d'observation est une étude qui explore la corrélation entre le tabagisme et le cancer du poumon. Ce type d'étude utilise généralement une enquête pour recueillir des observations sur la zone d'intérêt, puis effectuer une analyse statistique. Dans ce cas, les chercheurs devraient recueillir les observations des deux fumeurs et non-fumeurs, peut-être à travers une étude cas-témoins, puis de regarder le nombre de cas de cancer du poumon dans chaque groupe.

Les étapes de base pour une expérience sont les suivants:

1. planifier la recherche, y compris la détermination des sources d'information, la sélection des sujets de recherche, et éthiques considérations pour la recherche et méthode proposée,
2. Conception de l'expérience se concentrant sur le modèle du système et de l'interaction de variables indépendantes et dépendantes,
3. résumer un recueil d'observations à présenter leur communauté en supprimant les détails ( statistiques descriptives),
4. parvenir à un consensus sur ce que les observations nous disent sur le monde que nous observons ( inférence statistique),
5. document et présenter les résultats de l'étude.

Les niveaux de mesure

Voir: Stanley Stevens '"échelles de mesure" (1946): nominal, ordinal, intervalle, le rapport

Il ya quatre types de mesures ou échelles de mesure utilisées dans les statistiques. Les quatre types ou niveaux de mesure (nominal, ordinal, intervalle, et le rapport) ont différents degrés d'utilité en statistique recherche. mesures de rapport, où à la fois une valeur zéro et les distances entre les différentes mesures sont définies, offrent la plus grande flexibilité dans les méthodes statistiques qui peut être utilisé pour analyser les données. Mesures d'intervalles ont distances significatives entre les mesures, mais aucune valeur significative zéro (telles que les mesures de QI ou de mesures de température dans Fahrenheit). Mesures ordinales ont des différences entre les valeurs consécutives imprécises mais un ordre significatif à ces valeurs. Mesures nominales ont pas d'ordre de rang significatif parmi les valeurs.

Variables conformes seulement aux mesures nominales ou ordinales sont ainsi parfois appelés variables catégoriques, car ils ne peuvent raisonnablement être mesurés numériquement, alors que le ratio et par intervalles mesures sont regroupées sous quantitative ou variables continues en raison de leur nature numérique.

Les techniques statistiques

Certains bien connus statistiques essais et les procédures de recherche observations sont:

Disciplines spécialisées

Certains champs des statistiques d'utilisation d'enquête appliquées de façon extensive qu'ils ont terminologie spécialisée. Ces disciplines sont:

Statistiques constituent un outil de base clé dans les affaires et de fabrication ainsi. Il est utilisé pour comprendre des systèmes de mesure de la variabilité, des processus de contrôle (comme dans contrôle statistique du processus ou SPC), pour résumer les données et de prendre des décisions basées sur les données. Dans ces rôles, il est un outil essentiel, et peut-être le seul outil fiable.

Calcul statistique

Les augmentations rapides et soutenues dans la puissance de calcul à partir de la seconde moitié du 20ème siècle ont eu un impact considérable sur la pratique de la science statistique. Les premiers modèles statistiques étaient presque toujours à partir de la classe de modèles linéaires, mais des ordinateurs puissants, couplés avec numériques appropriés algorithmes , ont provoqué un regain d'intérêt pour modèles non linéaires (en particulier les réseaux de neurones et des arbres de décision) et la création de nouveaux types, tels que modèles linéaires généralisés et modèles multiniveaux.

Puissance de calcul accrue a également conduit à la popularité croissante des méthodes de calcul intensif basées sur des rééchantillonnage, comme les tests de permutation et de la bootstrap, tandis que les techniques telles que Échantillonnage de Gibbs ont fait des méthodes bayésiennes plus réalisable. La révolution informatique a des implications pour l'avenir des statistiques, avec un nouvel accent sur les statistiques "expérimentales" et "empiriques". Un grand nombre de fois à usage général et spécial progiciels statistiques sont maintenant disponibles pour les praticiens.

Abus

Il ya une perception générale que la connaissance statistique est bien trop souvent intentionnellement abusé, en trouvant des façons d'interpréter les données qui sont favorables au présentateur. Une phrase célèbre attribuée à Benjamin Disraeli est, " Il ya trois sortes de mensonges:. Mensonges, les sacrés mensonges et les statistiques »Et le président de Harvard Lawrence Lowell a écrit en 1909 que les statistiques, "comme les tartes de veau, sont bonnes si vous connaissez la personne qui les a rendus, et sont sûrs de les ingrédients."

Si diverses études semblent contredire les uns les autres, le public peut venir à se méfier de telles études. Par exemple, une étude peut suggérer qu'un régime ou une activité donnée soulève la pression artérielle , tandis qu'un autre peut suggérer qu'il abaisse la pression artérielle. L'écart peut provenir de subtiles variations dans la conception expérimentale, telles que les différences dans les groupes de patients ou des protocoles de recherche, qui ne sont pas facilement compréhensibles par le non-expert. (Rapports des médias omettent parfois cette information contextuelle vitale entièrement.)

En choisissant (ou de rejeter ou modifier) un certain échantillon, les résultats peuvent être manipulés; jeter aberrantes est un des moyens de le faire. Ces manipulations ne doivent pas être malveillant ou retors; ils peuvent provenir de préjugés involontaires du chercheur. Les graphiques utilisés pour résumer les données peuvent également être trompeurs.

Critiques profondes proviennent du fait que l'approche de tests d'hypothèses, largement utilisé dans de nombreux cas requis par la loi ou un règlement, oblige une hypothèse (la hypothèse nulle) à "favorisé", et peut également sembler exagérer l'importance de différences mineures dans les grandes études. Une différence qui est statistiquement très significative peut encore être d'aucune importance pratique. (Voir critique de tests d'hypothèses et controverse sur l'hypothèse nulle.)

Une réponse a été un plus grand accent sur la valeur p plus tout simplement de rapports si une hypothèse a été rejetée au niveau de signification donné. La valeur p, cependant, ne indique pas la taille de l'effet. Une autre approche de plus en plus courante consiste à signaler intervalles de confiance. Bien que ceux-ci sont produits à partir des mêmes calculs que les tests d'hypothèses ou p -values, ils décrivent à la fois la taille de l'effet et de l'incertitude qui l'entoure.