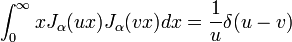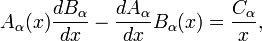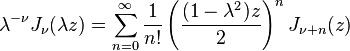Função de Bessel
Você sabia ...
Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Visite o site da SOS Children at http://www.soschildren.org/
Em matemática , as funções de Bessel, primeiro definida pelo matemático Daniel Bernoulli e generalizada por Friedrich Bessel, são soluções canônica y (x) de Bessel de equação diferencial :
para um número real ou complexo α arbitrária. O caso especial mais comum e é importante onde α é um número inteiro n, então α é referido como o fim da função de Bessel.
Embora α e -α produzir a mesma equação diferencial, é convencional para definir diferentes funções de Bessel para estes dois pedidos (por exemplo, de modo que as funções de Bessel na maior parte suaves são funções de α). Funções de Bessel também são conhecidas como funções cilindro ou cilíndricos harmónicas porque eles são encontrados na solução de A equação de Laplace em coordenadas cilíndricas.
Aplicações
A equação de Bessel surge quando encontrar soluções para separáveis E a equação de Laplace Equação de Helmholtz em cilíndricos ou esféricos coordenadas . Funções de Bessel são, portanto, particularmente importante para muitos problemas de propagação de ondas, potenciais estáticos, e assim por diante. Na resolução de problemas em sistemas de coordenadas cilíndricas, obtém-se funções de Bessel de ordem inteiro (α = n); em problemas esféricas, obtém-se uma meia-ordens inteiros (α = n + ½). Por exemplo:
- ondas electromagnéticas numa cilíndrica guia de ondas
- condução de calor num objecto cilíndrico.
- modos de vibração de uma circular fina (ou anulares) membrana artificial.
- problemas de difusão em uma treliça.
Funções de Bessel também têm propriedades úteis de outros problemas, tais como processamento de sinal (por exemplo, ver Síntese FM, Janela Kaiser, ou Filtro de Bessel).
Definições
Uma vez que esta é uma equação diferencial de segunda ordem, deve haver dois soluções linearmente independentes. Dependendo das circunstâncias, no entanto, várias formulações destas soluções é conveniente, e as diferentes variações são descritas abaixo.
Funções de Bessel do primeiro tipo: 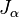
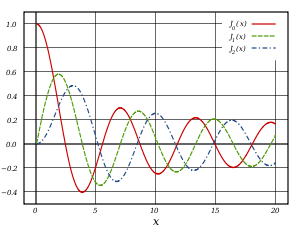
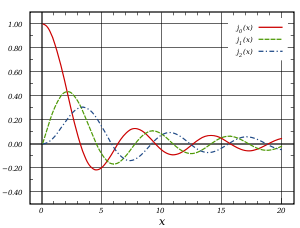
Funções de Bessel do primeiro tipo, denominado J α (x), são soluções da equação diferencial de Bessel que são finitos na origem (x = 0) para α inteiro não negativo, e divergem quando x tende a zero para não-inteiro negativo α. O tipo de solução (por exemplo, um inteiro ou não inteiro) e normalização de J α (x) são definidos pelas suas propriedades abaixo. Para soluções de ordem inteiros, é possível definir a função por sua série de Taylor expansão em torno de x = 0:
onde  é o função gama, uma generalização do fatorial função para valores não-inteiros. Para não inteiro α, um mais geral série de potência expansão é necessária. Os gráficos de funções de Bessel olhar mais ou menos como oscilando funções seno ou co-seno que se decompõem na proporção 1 / √ x (ver também as suas formas assintóticas abaixo), embora as suas raízes não são geralmente periódica, exceto assintoticamente para grandes x. (A série de Taylor, que indica
é o função gama, uma generalização do fatorial função para valores não-inteiros. Para não inteiro α, um mais geral série de potência expansão é necessária. Os gráficos de funções de Bessel olhar mais ou menos como oscilando funções seno ou co-seno que se decompõem na proporção 1 / √ x (ver também as suas formas assintóticas abaixo), embora as suas raízes não são geralmente periódica, exceto assintoticamente para grandes x. (A série de Taylor, que indica 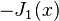 é o derivado de
é o derivado de 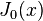 , Bem como
, Bem como 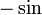 é o derivado de
é o derivado de 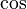 ; mais geralmente, o derivado de
; mais geralmente, o derivado de 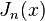 pode ser expressa em termos de
pode ser expressa em termos de 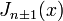 por as identidades abaixo ).
por as identidades abaixo ).
Para α não inteiros, as funções 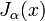 e
e 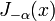 são linearmente independentes, e estão, por conseguinte, as duas soluções da equação diferencial. Por outro lado, para a ordem inteiro
são linearmente independentes, e estão, por conseguinte, as duas soluções da equação diferencial. Por outro lado, para a ordem inteiro 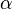 , A seguinte relação é válida:
, A seguinte relação é válida:
Isto significa que as duas soluções já não são linearmente independentes. Neste caso, é então encontrado na segunda solução linearmente independentes são a função de Bessel de segunda espécie, como discutido abaixo.
Integrais de Bessel
Outra definição da função de Bessel, para valores inteiros de 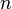 , É possível usando uma representação integral:
, É possível usando uma representação integral:
Esta foi a abordagem que Bessel utilizado e, a partir dessa definição, ele derivou várias propriedades da função.
Outra representação integral é:
Relação à série hipergeométrica
As funções de Bessel pode ser expressa em termos de séries hipergeométricas como
Esta expressão está relacionada com o desenvolvimento de funções de Bessel, em termos de Função de Bessel-Clifford.
Funções de Bessel do segundo tipo: 
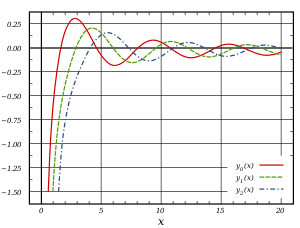
As funções de Bessel de segunda espécie, denotado por α Y (X), são soluções da equação diferencial de Bessel. Eles são singular ( infinito) na origem (x = 0).
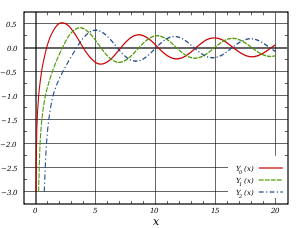
Α Y (X) é, às vezes também chamada a função Neumann, e é por vezes designado por α em vez de N (X). Para α não inteiros, ela está relacionada com J α (x) por:
No caso de ordem inteiro n, a função é definida tomando o limite como um número não inteiro α tende a n ':
que tem o resultado (em forma integral)
Para o caso de α não inteiros, a definição de α Y (x) é redundante (tal como resulta da sua definição acima). Por outro lado, quando α é um número inteiro, Y α (x) é a segunda solução linearmente independente da equação de Bessel; Além disso, como foi o caso de forma semelhante para as funções do primeiro tipo, a seguinte relação é válida:
Ambos α J (x) e α Y (x) são funções holomorfas de x no plano complexo corte ao longo do eixo real negativo. Quando α é um número inteiro, não há ponto de ramificação, e as funções de Bessel são funções inteiras de x. Se x é mantido fixo, então as funções de Bessel são funções inteiras de α.
Funções de Hankel: 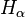
Outra formulação importante das duas soluções linearmente independentes a equação de Bessel são funções de Hankel α H (1) (X) e α H (2) (X), definida por:
onde i é a unidade imaginária . Estas combinações lineares são também conhecidas como funções de Bessel do terceiro tipo; eles são duas soluções linearmente independentes da equação diferencial de Bessel. As funções de Hankel do primeiro e segundo tipo são usados para expressar outward- e para dentro de propagação de onda cilíndrica soluções da equação de onda cilíndrica, respectivamente (ou vice-versa, dependendo do convenção de sinal para o frequência). Eles são nomeados após Hermann Hankel.
Usando as relações anteriores podem ser expressas como:
Se α é um número inteiro, o limite tem de ser calculada. As seguintes relações são válidas, se α é um inteiro ou não:
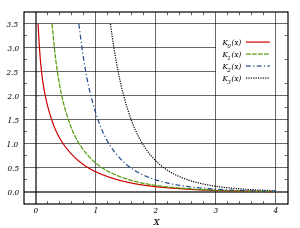
Funções de Bessel de modificação: 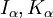
As funções de Bessel são válidos mesmo para complexos argumentos x, e um caso especial importante é a de um argumento puramente imaginário. Neste caso, as soluções para a equação de Bessel são chamados as funções de Bessel modificadas (ou, ocasionalmente as funções de Bessel hiperbólicas) do primeiro e segundo tipo, e são definidos por:
Estes são escolhidos para ser de valor real para argumentos reais x. A expansão em série para que α (x) é, portanto, semelhante ao usado para α j (x), mas sem o alternada (-1) m fator.
I α (x) e K α (X) são as duas soluções linearmente independentes para a equação de Bessel modificada:
Ao contrário das funções de Bessel ordinárias, que são oscilantes como funções de um argumento real, eu α e K α são exponencialmente crescente e funções em decomposição, respectivamente. Como a função de Bessel J α comum, a função que eu α vai a zero em x = 0 para α> 0 e é finito em x = 0 para α = 0. Analogamente, K α diverge em x = 0.
 |  |
A função de Bessel modificada de segundo tipo também tem sido chamado pelos nomes agora-raros:
- Função Basset
- função de Bessel modificada do terceiro tipo
- Função MacDonald
Funções de Bessel esféricas: 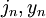
Quando a solução de Equação de Helmholtz em coordenadas esféricas por separação de variáveis, a equação radial tem a forma:
As duas soluções linearmente independentes desta equação são chamados de Bessel esférica funciona j n y e n, e estão relacionados com a funções de Bessel J n normal e Y n por:
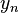 é também indicada
é também indicada 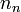 ou η n; alguns autores chamam essas funções as funções Neumann esféricas.
ou η n; alguns autores chamam essas funções as funções Neumann esféricas.
As funções de Bessel esféricas também pode ser escrita como:
A primeira função de Bessel esférica 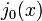 também é conhecido como o (unnormalized) função sinc. As primeiras funções de Bessel esféricas são:
também é conhecido como o (unnormalized) função sinc. As primeiras funções de Bessel esféricas são:
e
Há também análogos esféricos das funções de Hankel:
Na verdade, não são simples expressões de forma fechada para as funções de Bessel ordem semi-inteiro em termos de padrão de funções trigonométricas , e, portanto, para as funções de Bessel esféricas. Em particular, para inteiros não negativos n:
e H N (2) é o complexo-conjugado deste (para x real). Segue-se, por exemplo, que j 0 (x) = sen (x) / x e y 0 (x) = -cos (x) / x, e assim por diante.
Funções Riccati-Bessel: 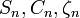
Funções Riccati-Bessel apenas ligeiramente diferem de funções de Bessel esféricas:
Eles satisfazem a equação diferencial:
Esta equação diferencial, e as soluções de Riccati-Bessel, surge o problema de dispersão de ondas electromagnéticas por uma esfera, como conhecido Mie espalhamento após a primeira solução publicada por Mie (1908). Ver, por exemplo Du (2004) para os desenvolvimentos recentes e referências.
Seguinte Debye (1909), a notação 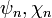 é por vezes usado em vez de
é por vezes usado em vez de 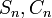 .
.
Formas assintóticas
As funções de Bessel tem a seguinte formas assintóticas para α não negativo. Para as pequenas argumentos 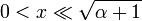 , Obtém-se:
, Obtém-se:
onde γ é a Constante de Euler-Mascheroni (0,5772 ...) e indica a Γ função gama. Para grandes argumentos 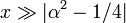 , Eles tornam-se:
, Eles tornam-se:
(Para α = 1/2 estas fórmulas são exatas; ver as funções de Bessel esféricas acima.) Formas assintóticas para os outros tipos de função de Bessel seguem diretamente das relações acima. Por exemplo, para grande 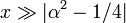 , As funções de Bessel modificadas tornar-se:
, As funções de Bessel modificadas tornar-se:
enquanto para as pequenas argumentos 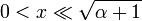 , Eles tornam-se:
, Eles tornam-se:
Propriedades
Por fim inteiro α = n, J n é muitas vezes definido através de um Séries de Laurent para uma função geradora:
uma abordagem utilizada por PA Hansen em 1843. (Isso pode ser generalizado a ordem não inteira por integração de contorno ou outros métodos). Outra relação importante para as ordens de inteiros é a Identidade de Jacobi-Anger:
o qual é usado para expandir um onda plana como uma soma de ondas cilíndricas, ou para encontrar o Séries de Fourier de um tom modulado Sinal de FM.
As funções α J, Y, α α H (1), e α H (2) tudo o satisfazer relações de recorrência:
em que Z indica a J, Y, H (1), ou H (2). (Estas duas identidades são frequentemente combinados, por exemplo, adicionados ou subtraídos, para produzir várias outras relações.) Deste modo, por exemplo, pode-se calcular funções de Bessel de ordem mais elevada (ou derivados maiores) Considerando os valores em ordens mais baixas (inferiores ou derivados ). Em particular, segue-se que:
Funções de Bessel modificadas siga relações semelhantes:
e
A relação de recorrência lê
em que C indica que α α ou e απ i K α. Estas relações de recorrência são úteis para problemas de difusão discretos.
Porque se torna equação de Bessel Hermitiana (auto-adjunta) se for dividido por x, as soluções devem satisfazer uma relação de ortogonalidade para as condições de contorno apropriadas. Em particular, segue-se que:
onde α> -1, δ m, n é o Delta de Kronecker e α u, m é o m-ésimo zero da α J (x). Esta relação ortogonalidade pode então ser usado para extrair os coeficientes no Séries de Fourier-Bessel, em que uma função é expandido na base das funções J α (x α u, M) para α fixo e variando m. (Uma relação análoga para as funções de Bessel esféricas segue imediatamente.)
Outra relação de ortogonalidade é a equação de fechamento:
para α> -1/2 e onde δ é a Delta de Dirac. Esta propriedade é usada para a construção de uma função arbitrária a partir de uma série de funções de Bessel por meio do Hankel transformar. Para as funções de Bessel esféricas a relação ortogonalidade é:
para α> 0.
Outra propriedade importante das equações de Bessel, que decorre A identidade de Abel, envolve a Wronskiano das soluções:
onde A e α α B são quaisquer duas soluções da equação de Bessel, e C é uma constante α independente de x (que depende α e nas funções de Bessel específicas consideradas). Por exemplo, se A = J α α α e B = Y α, então C é α 2 / π. Isso também vale para as funções de Bessel modificadas; por exemplo, se A = I α α e B α = K α, então C é α -1.
(Existe um grande número de outros integrais e identidades conhecidas que não são aqui reproduzidas, mas que podem ser encontrados nas referências).
Multiplicação teorema
As funções de Bessel obedecer a um multiplicação teorema
onde 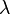 e
e 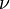 pode ser tomada como números complexos arbitrários. Uma forma semelhante pode ser dada para
pode ser tomada como números complexos arbitrários. Uma forma semelhante pode ser dada para 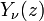 e etc. Ver
e etc. Ver
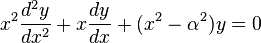
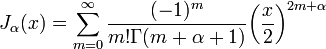
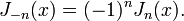
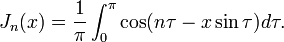
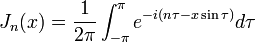
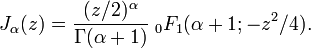
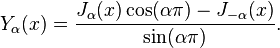
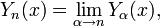
![Y_n (x) = \ frac {1} {\ pi} \ int_ {0} ^ {\ pi} \ sin (x \ sin \ theta - n \ theta) d \ theta - \ frac {1} {\ pi} \ int_ {0} ^ {\ infty} \ left [e ^ {nt} + (-1) ^ ne ^ {- nt} \ right] e ^ {- x \ t} sinh dt.](../../images/208/20863.png)
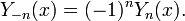
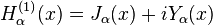
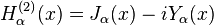

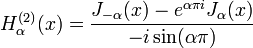
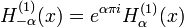
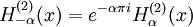
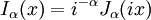
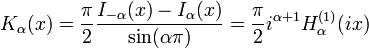
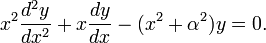
![x ^ 2 \ frac {d ^ 2 y} {dx ^ 2 + 2x} \ frac {dy} {dx} + [x ^ 2 - n (n + 1)] y = 0.](../../images/209/20907.png)
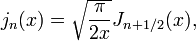
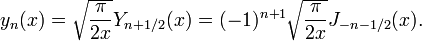
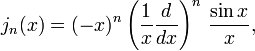

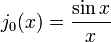
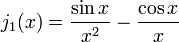
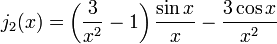
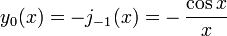
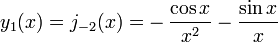
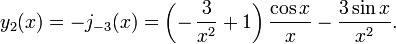
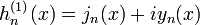
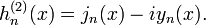
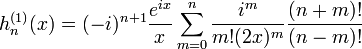

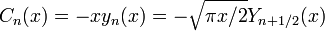
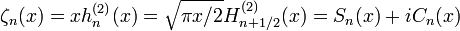
![x ^ 2 \ frac {d ^ 2 y} {dx ^ 2} + [x ^ 2 - n (n + 1)] y = 0](../../images/209/20927.png)
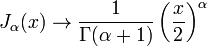
![Y_ \ alpha (x) \ rightarrow \ left \ {\ begin {matrix} \ frac {2} {\ pi} \ left [\ ln (x / 2) + \ gamma \ right] & \ mbox {if} \ alpha = 0 \\ \\ - \ frac {\ Gamma (\ alpha)} {\ pi} \ left (\ frac {2} {x} \ right) ^ \ alpha & \ mbox {if} \ alpha> 0 \ end {matrix} \ right.](../../images/209/20932.png)
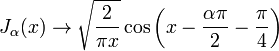
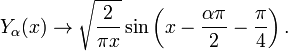
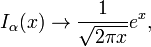
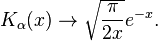


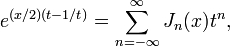
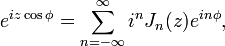
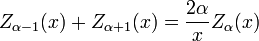
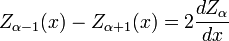
![\ Left (\ frac {d} {x dx} \ right) ^ m \ left [x ^ \ alpha Z _ {\ alpha} (x) \ right] = x ^ {\ alpha - m} Z _ {\ alpha - m } (x)](../../images/209/20944.png)
![\ Left (\ frac {d} {x} dx \ right) ^ m \ left [\ frac {Z_ \ alpha (x)} {x ^ \ alpha} \ right] = (-1) ^ m \ frac {Z_ {\ alpha + m} (x)} {x ^ {\ alpha + m}}](../../images/209/20945.png)
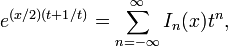
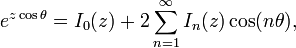
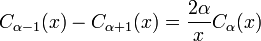
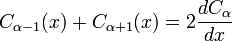
![\ Int_0 ^ 1 x J_ \ alpha (x u _ {\ alpha, m}) J_ \ alpha (x u _ {\ alpha, n}) dx = \ frac {\ delta_ {m, n}} {2} [J_ { \ alpha + 1} (u _ {\ alpha, m})] ^ 2 = \ frac {\ delta_ {m, n}} {2} [J _ {\ alpha} '(u _ {\ alpha, m})] ^ 2,](../../images/209/20950.png)