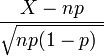Distribuição binomial
Você sabia ...
Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas de todo o mundo. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
Função massa de probabilidade 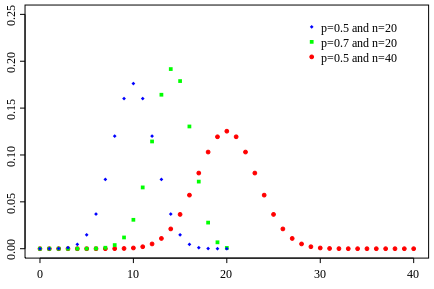 | |
Função de distribuição cumulativa 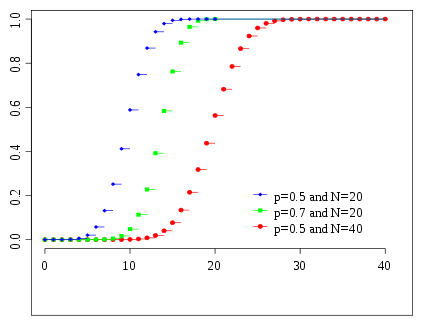 As cores combinam a imagem acima | |
| Parâmetros | 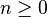 número de tentativas ( inteiro ) número de tentativas ( inteiro ) 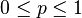 probabilidade de sucesso ( verdadeiro ) probabilidade de sucesso ( verdadeiro ) |
|---|---|
| Apoio | 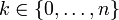 |
| PMF | 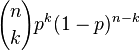 |
| CDF | 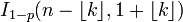 |
| Significar | 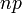 |
| Mediano | um de  |
| Modo | 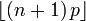 |
| Variação | 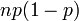 |
| Assimetria | 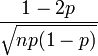 |
| Ex. curtose | 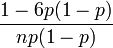 |
| Entropy | 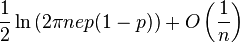 |
| MGF |  |
| CF | 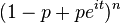 |
Em teoria da probabilidade e estatística , a distribuição binomial é a distribuição de probabilidade discreta do número de sucessos em uma seqüência de n sim / não experiências independentes, cada uma das quais rende sucesso com probabilidade p. Tal sucesso / fracasso experimento também é chamado de um experimento ou Bernoulli Julgamento Bernoulli. Na verdade, quando n = 1, a distribuição binomial é um Distribuição de Bernoulli. A distribuição binomial é a base para o popular teste binomial de significância estatística. Uma distribuição binomial não deve ser confundido com um distribuição bimodal.
Exemplos
Um exemplo elementar é esta: Role um padrão morrer dez vezes e contar o número de seis. A distribuição deste número aleatório é uma distribuição binomial com n = 10 e p = 1/6.
Como outro exemplo, suponha 5% de uma população muito grande para ser de olhos verdes. Você escolhe aleatoriamente 100 pessoas. O número de pessoas de olhos verdes que você escolhe é uma variável aleatória X que segue uma distribuição binomial com n = 100 e p = 0,05.
Especificação
Função massa de probabilidade
Em geral, se a variável aleatória K segue a distribuição binomial com parâmetros n e p, podemos escrever K ~ B (n, p). A probabilidade de obter exactamente k sucessos em n ensaios é dada pela função massa de probabilidade:
para k = 0, 1, 2, ..., n e onde
é o coeficiente binomial (daí o nome da distribuição) "n escolher K" (também denotado C (n, k) ou n C k). A fórmula pode ser entendida da seguinte maneira: queremos k sucessos (p k) e n - falhas K (1 - p) n - k. No entanto, os sucessos k pode ocorrer em qualquer lugar entre os n tentativas, e não são C (n, k), diferentes formas de distribuição k sucessos em uma sequência de n ensaios.
Ao criar tabelas de referência para a probabilidade de distribuição binomial, geralmente o quadro é preenchido em até n / 2 valores. Isto é porque para k> n / 2, a probabilidade pode ser calculada por seu complemento como
Então, é preciso olhar para um k diferente e uma diferente p (o binômio não é simétrica em geral).
Função de distribuição cumulativa
O função de distribuição cumulativa pode ser expressa em termos de regularizada função beta incompleta, como se segue:
fornecida k é um inteiro 0 e ≤ k ≤ n. Se x não é necessariamente um número inteiro ou não necessariamente positivo, pode-se expressar da seguinte maneira:
Para k ≤ np, limites superiores para a cauda inferior da função de distribuição pode ser derivada. Em particular, A desigualdade de Hoeffding produz o limite
e A desigualdade de Chernoff pode ser usado para derivar o limite
Média, variância, eo modo
Se X ~ B (n, p) (isto é, X é uma variável aleatória binomial distribuído), em seguida, o valor esperado de X é
ea variância é
Este facto é facilmente comprovada como se segue. Suponha primeiro que temos exatamente um julgamento Bernoulli. Nós temos dois resultados possíveis, 1 e 0, com o primeiro tendo probabilidade p eo segundo tendo probabilidade 1 - p; a média para este julgamento é dado por μ = p. Utilizando a definição de variância , temos
Agora, suponha que queremos que a variância para n tais ensaios (ou seja, para a distribuição binomial geral). Uma vez que os ensaios são independentes, podemos acrescentar os desvios para cada julgamento, dando
O modo de X é o maior inteiro menor do que ou igual a (n + 1) p; se m = (n + 1) p é um número inteiro, então m - 1 e m são ambos os modos.
Derivações explícitas de média e variância
Obtivemos essas quantidades dos primeiros princípios. Certas quantias específicas ocorrem nessas duas derivações. Nós reorganizar os montantes e prazos para que resume unicamente sobre as funções completas de massa de probabilidade binomial ( PMF ) surgem, que estão sempre a unidade
Significar
Nós aplicamos a definição do valor esperado de uma variável aleatória discreta para a distribuição binomial
O primeiro termo da série (com índice k = 0) tem valor 0 desde o primeiro fator, k, é zero. Pode, assim, ser descartados, ou seja, podemos alterar o limite inferior para: k = 1
Nós puxado fatores de N e K fora dos fatoriais, e um poder de p foi cindida. Estamos nos preparando para redefinir os índices.
Nós renomear m = n - 1 e s = k - 1. O valor da soma não é alterado pelo presente, mas agora se torna facilmente identificável
A soma resultante é uma soma sobre um binômio completa pmf (de uma ordem inferior à soma inicial, como acontece). Assim
Variação
Pode-se mostrar que a variância é igual a (ver: variância, 10. fórmula computacional para variância ):
Em usando esta fórmula, vemos que agora também precisa do valor esperado de X 2, que é
Nós podemos usar nossa experiência adquirida em derivar acima da média. Nós sabemos como processar um fator de k. Isso nos leva tão longe como
(Mais uma vez, com m = n - 1 e s = k - 1). Podemos dividir a soma em duas somas separadas e reconhecemos cada um
A primeira soma é idêntico em forma à que calculado no Média (acima). Ele resume a pf. A segunda soma é a unidade.
Usando este resultado na expressão para a variância, juntamente com a média (E (X) = NP), obtemos
Relação com outras distribuições
Somas de binômios
Se X ~ B (n, p) e Y ~ B (m, p) são variáveis independentes binomial, então X + Y é de novo uma variável binomial; sua distribuição é
Aproximação normal
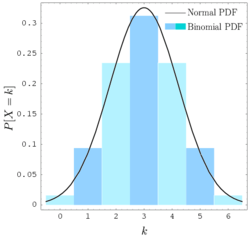
Se n for suficientemente grande, a inclinação da distribuição não é muito grande, e um adequado correcção de continuidade é utilizado, em seguida, uma excelente aproximação para B (n, p) é dada pela distribuição normal
Vário regras de polegar pode ser utilizada para decidir se n é suficientemente grande. Uma regra é que ambos NP e n (1 - P) deve ser superior a 5. No entanto, o número específico varia de fonte para a fonte, e depende de quão boa é uma aproximação uma quer; Algumas fontes dão 10. Outra regra comumente usado sustenta que a aproximação normal acima é apropriada somente se
O que se segue é um exemplo de aplicação de um correção de continuidade: Suponha que se deseja calcular Pr (X ≤ 8) para uma variável aleatória X binomial. Se Y tem uma distribuição determinada pela aproximação normal, em seguida, Pr (X ≤ 8) é aproximada por Pr (Y ≤ 8,5). A adição de 0,5 é a correcção de continuidade; a aproximação normal sem correção dá resultados consideravelmente menos precisos.
Esta aproximação é uma enorme economia de tempo (cálculos exatos com grande n são muito oneroso); Historicamente, foi a primeira utilização de uma distribuição normal, introduzido em O livro de Abraham de Moivre A Doutrina da Chances em 1733. Hoje em dia, ele pode ser visto como uma consequência da teorema do limite central desde B (n, p) é uma soma de n independente, identicamente distribuídos 0-1 variáveis indicadoras.
Por exemplo, suponha que você provar n pessoas, de uma grande população de forma aleatória e perguntar-lhes se concordam com uma determinada declaração. A proporção de pessoas que concordam, claro, irá depender da amostra. Se você amostrados grupos de n pessoas repetidamente e verdadeiramente aleatoriamente, as proporções iria seguir uma distribuição normal com média aproximada igual a verdadeira proporção p de acordo na população e com desvio padrão σ = (p (1 - p) n) 1 / 2. Grande o tamanho das amostras n são boas, porque o desvio padrão, como uma percentagem do valor esperado, torna-se menor, o que permite um cálculo mais preciso do parâmetro desconhecido p.
Poisson aproximação
A distribuição binomial converge para a distribuição de Poisson como o número de ensaios vai para infinito quando o np produto permanece fixo. Por conseguinte, a distribuição de Poisson com parâmetro λ = NP pode ser usado como uma aproximação para B (n, p) da distribuição binomial se n for suficientemente grande e p é suficientemente pequena. De acordo com duas regras de ouro, esta aproximação é bom se n ≥ 20 e P ≤ 0,05, ou se n ≥ 100 e ≤ 10 np.
Limites da distribuição binomial
- Como n se aproxima ∞ e P se aproxima de 0, enquanto permanece fixo na NP λ> 0 ou pelo menos se aproxima NP λ> 0, em seguida, o binomial (n, p) de distribuição se aproxima da distribuição de Poisson com λ valor esperado.
- Como n se aproxima ∞ p enquanto permanece fixo, a distribuição de
- se aproxima da distribuição normal com valor esperado 0 e variância 1 (este é apenas um caso específico do Teorema do Limite Central).
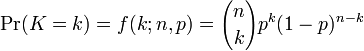
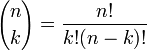
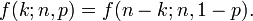
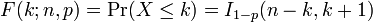
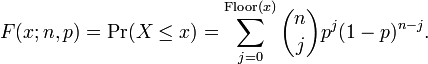
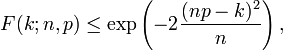
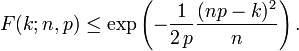
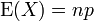
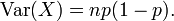
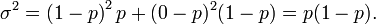
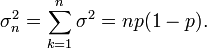
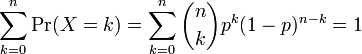
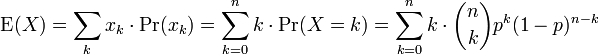
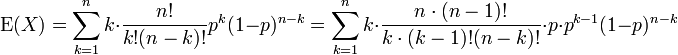
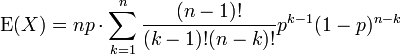
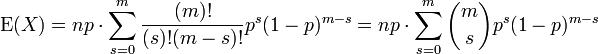

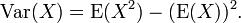
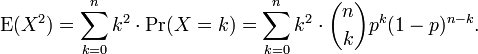
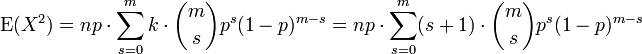
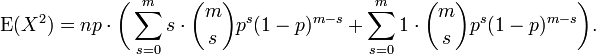
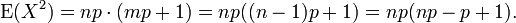
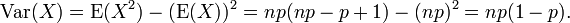
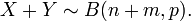
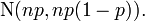
![\ Mu pm \ 3 \ sigma = np \ pm 3 \ sqrt {np (1-p)} \ in [0, n].](../../images/195/19591.png)