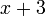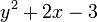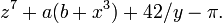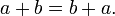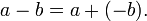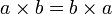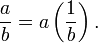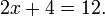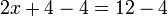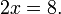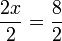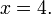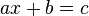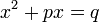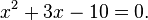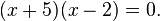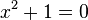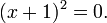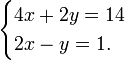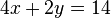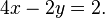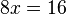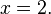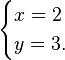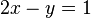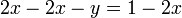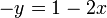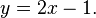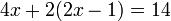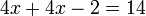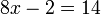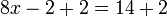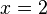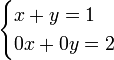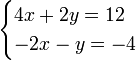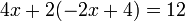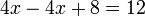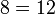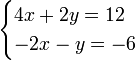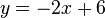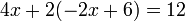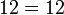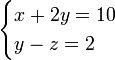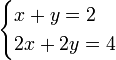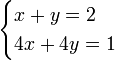Álgebra elementar
Fundo para as escolas Wikipédia
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/
Álgebra elementar é uma forma fundamental e relativamente básico de álgebra ensinado aos estudantes que se presume ter pouco ou nenhum conhecimento formal da matemática além de aritmética . Enquanto na aritmética apenas números e suas operações aritméticas (como +, -, ×, ÷) ocorrem, em álgebra um também usa símbolos (como x e y, ou a e b) números para denotam. Estes são chamados variáveis. Isto é útil porque:
- Ele permite a generalização da aritmética equações (e desigualdades ) para ser indicado como leis (como
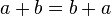 para toda a e b), e, portanto, é o primeiro passo para o estudo sistemático das propriedades do sistema de números reais .
para toda a e b), e, portanto, é o primeiro passo para o estudo sistemático das propriedades do sistema de números reais . - Ela permite que os números de referência para que não são conhecidos. No contexto de um problema, uma variável pode representar um certo valor das quais é incerto, mas pode ser resolvido por meio da formulação e manipulação de equações.
- Ele permite a exploração de relações matemáticas entre quantidades (como "se você vender bilhetes x, então seu lucro será
 dólares ").
dólares ").
Estes três são as principais vertentes da álgebra elementar, que devem ser distinguidos de álgebra abstrata , um tópico mais avançado geralmente ensinado aos estudantes universitários.
Em álgebra elementar, um " . expressão "pode conter números, variáveis e operações aritméticas Estes são geralmente escrito (por convenção) com termos« de maior poder "sobre a esquerda (ver polinomial ); alguns exemplos são:
Em álgebra mais avançado, uma expressão pode também incluir funções elementares.
Um " equação "é a alegação de que duas expressões são iguais. Algumas equações são verdadeiro para todos os valores das variáveis envolvidas (tais como 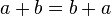 ); tais equações são chamados " "." identidades equações condicionais "são verdadeiras apenas para alguns valores das variáveis envolvidas:
); tais equações são chamados " "." identidades equações condicionais "são verdadeiras apenas para alguns valores das variáveis envolvidas: 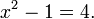 Os valores das variáveis que tornam a equação verdadeira são chamados de "soluções" da equação.
Os valores das variáveis que tornam a equação verdadeira são chamados de "soluções" da equação.
Leis da álgebra elementar
- Comutativa propriedade de adição
- A subtracção é o inverso da adição.
- Para subtrair é a mesma que para adicionar um número negativo :
- Exemplo: se
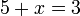 em seguida
em seguida 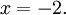
- Propriedade comutativa da multiplicação
- Divisão é o inverso da multiplicação.
- Para fractura é o mesmo que para multiplicar por um recíproco:
- Exponenciação não é uma operação comutativa.
- Portanto exponenciação tem um par de operações reversíveis: logaritmo e exponenciação com expoentes fracionários (por exemplo, raízes quadradas ).
- Exemplos: Se
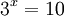 em seguida
em seguida 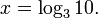 Se
Se 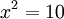 em seguida
em seguida 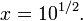
- Exemplos: Se
- As raízes quadradas de números negativos não existe no sistema de número real. (Veja: sistema de número complexo )
- Portanto exponenciação tem um par de operações reversíveis: logaritmo e exponenciação com expoentes fracionários (por exemplo, raízes quadradas ).
- Associativa propriedade de adição:
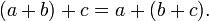
- Associatividade da multiplicação:
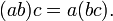
- Propriedade distributiva da multiplicação em relação à adição:
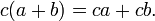
- Propriedade distributiva de exponenciação com respeito a multiplicação:
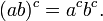
- Como combinar expoentes:
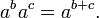
- Poder de uma propriedade poder de expoentes:
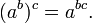
Leis da igualdade
- Se
 e
e 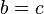 , Então
, Então  ( transitividade de igualdade).
( transitividade de igualdade).  ( reflexividade da igualdade).
( reflexividade da igualdade). - Se
 em seguida
em seguida 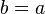 ( simetria da igualdade).
( simetria da igualdade).
Outras leis
- Se
 e
e 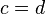 em seguida
em seguida 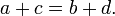
- Se
 em seguida
em seguida 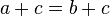 para qualquer c (propriedade além da igualdade).
para qualquer c (propriedade além da igualdade).
- Se
- Se
 e
e 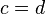 em seguida
em seguida 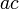 =
= 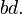
- Se
 em seguida
em seguida 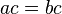 para qualquer c (propriedade multiplicação de igualdade).
para qualquer c (propriedade multiplicação de igualdade).
- Se
- Se dois símbolos são iguais, então pode ser substituído para o outro à vontade (princípio da substituição).
- Se
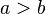 e
e 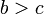 em seguida
em seguida 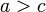 (Transitividade de desigualdade).
(Transitividade de desigualdade). - Se
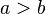 em seguida
em seguida 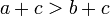 para qualquer c.
para qualquer c. - Se
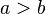 e
e 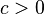 em seguida
em seguida 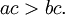
- Se
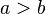 e
e 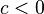 em seguida
em seguida 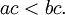
Exemplos
Equações lineares em uma variável
As equações mais simples de resolver são equações lineares que têm apenas uma variável. Eles contêm apenas números constantes e uma única variável, sem um expoente. Por exemplo:
A técnica fundamental é somar, subtrair, multiplicar ou dividir ambos os lados da equação pelo mesmo número, a fim de isolar a variável de um lado da equação. Uma vez que a variável é isolado, o outro lado da equação é o valor da variável. Por exemplo, subtraindo 4 de ambos os lados da equação acima:
o que simplifica a:
Dividindo ambos os lados por 2:
simplifica para a solução:
O caso geral,
segue o mesmo formato para a solução:
Equações de segundo grau
Equações quadráticas pode ser expressa na forma ax 2 + bx + c = 0, em que um não é zero (se fosse zero, então a equação quadrática não seria mas linear ). Devido a isso uma equação quadrática devem conter o termo ax 2, que é conhecido como o termo quadrático. Daí a ≠ 0, e assim podemos dividir por um e reorganizar a equação na forma padrão
onde p = b / a e q = - c / a. Resolver este, por um processo conhecido como completar o quadrado, leva à fórmula quadrática .
Equações de segundo grau também pode ser resolvido usando fatoração (o processo inverso do que é expansão, mas para dois Termos lineares é por vezes designado foiling). Como um exemplo de factoring:
Que é a mesma coisa que
Daqui resulta a partir da propriedades do produto ou zero que x = 2 x = -5 ou são as soluções, uma vez que precisamente um dos factores deve ser igual a zero, . Todas as equações de segundo grau terão duas soluções no número complexo sistema, mas não precisa ter qualquer no número real do sistema. Por exemplo,
não tem solução número real já que nenhum número real ao quadrado é igual a -1. Às vezes uma equação quadrática tem uma raiz de multiplicidade 2, tais como:
Para esta equação, -1 é uma raiz de multiplicidade dois.
Sistema de equações lineares
No caso de um sistema de equações lineares , como, por exemplo, duas equações em duas variáveis, é muitas vezes possível encontrar as soluções de ambas as variáveis que satisfaçam as equações.
Primeiro método de encontrar uma solução
Um exemplo de um sistema de equações lineares poderia ser a seguinte:
Multiplicando os termos do segundo equação por 2:
Somando as duas equações em conjunto para obter:
o que simplifica a
Uma vez que o facto de que é conhecida x = 2, então é possível deduzir que y = 3 por qualquer uma das duas equações originais (usando dois em vez de x) A solução completa para este problema é, em seguida,
Note que esta não é a única maneira de resolver este sistema específico; y poderia ter sido resolvido antes de x.
Segundo método de encontrar uma solução
Outra maneira de resolver o mesmo sistema de equações lineares é por substituição.
Um equivalente de Y pode ser deduzida utilizando uma das duas equações. Usando a segunda equação:
Subtraindo 2x de cada lado da equação:
e multiplicando por -1:
Utilizando este valor y na primeira equação no sistema original:
Adicionando duas em cada lado da equação:
o que simplifica a
Utilizando este valor numa das equações, a mesma solução que no método anterior é obtido.
Note que esta não é a única maneira de resolver este sistema específico; neste caso, bem como, y poderia ter sido resolvido antes x.
Outros tipos de sistemas de equações lineares
Sistemas insolúveis
No exemplo acima, é possível encontrar uma solução. No entanto, também existem sistemas de equações que não possuem uma solução. Um exemplo óbvio seria:
A segunda equação do sistema não tem uma solução possível. Portanto, este sistema não pode ser resolvido. No entanto, nem todos os sistemas incompatíveis são reconhecidos à primeira vista. Como um exemplo, o seguinte sistema é estudada:
Ao tentar solucionar este (por exemplo, usando o método de substituição acima), a segunda equação, após a adição de - 2 x em ambos os lados e multiplicando por -1, resulta em:
E usar este valor para y na primeira equação:
Não há variáveis são deixados, ea igualdade não é verdade. Isto significa que a primeira equação não pode proporcionar uma solução para o valor de y obtido na segunda equação.
Sistemas indeterminados
Existem também os sistemas que têm soluções múltiplas ou infinitos, em oposição a um sistema com uma solução única (ou seja, dois valores exclusivos para x e y) Por exemplo:
Isolando y na segunda equação:
E usando esse valor na primeira equação no sistema:
A igualdade é verdade, mas não fornece um valor para x. Com efeito, pode-se facilmente verificar (por apenas preencher alguns valores de x) que, para qualquer x não é uma solução, enquanto y = x + -2 6. Existem infinitas soluções para este sistema.
Ao longo e Sistemas indeterminados
Sistemas com mais variáveis do que o número de equações lineares não tem uma solução única. Um exemplo de um tal sistema é
Um tal sistema é chamado subdeterminada; quando se tenta encontrar uma solução, uma ou mais variáveis só pode ser expressa em relação a outras variáveis, mas não pode ser determinada numericamente. Aliás, um sistema com um maior número de equações que variáveis, em que necessariamente algumas equações são somas ou múltiplos de outras pessoas, é chamado sobredeterminado.
Relação entre Solvabilidade e Multiplicidade
Dado qualquer sistema de equações lineares, há uma relação entre multiplicidade e resolubilidade.
Se uma equação é um múltiplos do outro (ou, mais geralmente, uma soma de múltiplos de outras equações), então o sistema de equações lineares é indeterminado, o que significa que o sistema possui infinitas soluções. Exemplo:
Quando a multiplicidade é apenas parcial (o que significa que, por exemplo, apenas os lados esquerdos das equações são múltiplos, enquanto os lados da mão direita ou não pelo mesmo número), em seguida, o sistema é insolúvel. Por exemplo, em
os segundos rendimentos equação que x + y = 1/4 que está em contradição com a primeira equação. Esse sistema também é chamado inconsistente na linguagem da álgebra linear . Ao tentar resolver um sistema de equações lineares é geralmente uma boa idéia para verificar se uma equação é um múltiplo do outro. Se esta é precisamente isso, a solução não pode ser unicamente determinada. Se esta é apenas parcialmente, a solução não existe.
Isto, no entanto, não significa que as equações deve ser múltiplos de cada um possa ter uma solução, como mostrado nas secções anteriores; por outras palavras: multiplicidade num sistema de equações lineares não é um condição necessária para a resolubilidade.