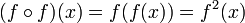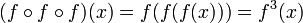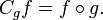Composição de função
Informações de fundo
Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Patrocínio da criança ajuda as crianças uma a uma http://www.sponsor-a-child.org.uk/ .
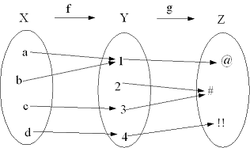
Em matemática , uma função composta, formada pela composição de uma função em um outro, representa a aplicação do primeiro para o resultado da aplicação desta última para o argumento do compósito. As funções f: X → Y eg: Y → Z pode ser composto por primeiro aplicar f a um argumento x e, em seguida, aplicar g para o resultado. Assim obtém-se uma função g o f: X → Z definido por (g o f) (x) = g (f (x)) para todo x em X. A notação g o f é lido como "círculo g f", ou "g composto com f", "g seguinte f", ou apenas "g de f".
A composição de funções é sempre associativa . Isto é, se f, g, e h são três funções com domínios e codomains adequadamente escolhidas, em seguida, de f o (g o h) = (f o g) o h. Como não há distinção entre as escolhas de colocação de parênteses, eles podem ser deixados com segurança fora.
As funções G e F comutar uns com os outros, se g o f = f o g. Em geral, a composição de funções não será conmutativo. Comutatividade é uma propriedade especial, alcançada somente por funções específicas, e muitas vezes em circunstâncias especiais. Por exemplo,  apenas quando
apenas quando 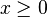 . Mas funções inverso sempre comutar para produzir o mapeamento de identidade.
. Mas funções inverso sempre comutar para produzir o mapeamento de identidade.
Derivados de composições que envolvem funções diferenciáveis pode ser encontrado usando a regra da cadeia. Derivados "superior" de tais funções são dadas por A fórmula de Faa di de Bruno.
Exemplo
Como um exemplo, suponha que a elevação de um avião no instante t é dado pela função de h (t) e que a concentração de oxigénio na elevação x é dado pela função c (x). Em seguida, (c o h) (t) descreve a concentração de oxigênio ao redor do avião no momento t.
Poderes funcionais
Se 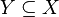 em seguida
em seguida  pode compor com ele mesmo; esta é por vezes designado
pode compor com ele mesmo; esta é por vezes designado 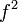 . Assim:
. Assim:
Composição repetida de uma função com a própria é chamada função de iteração.
Os funcionais poderes 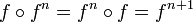 para naturais
para naturais 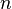 siga imediatamente.
siga imediatamente.
- Por convenção,
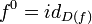
 o mapa de identidade no domínio de
o mapa de identidade no domínio de 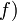 .
. - Se
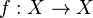 admite uma função inversa , poderes funcionais negativos
admite uma função inversa , poderes funcionais negativos 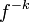
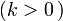 são definidos como o poder oposto da função inversa,
são definidos como o poder oposto da função inversa, 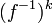 .
.
Nota: Se f leva seus valores em uma anel (em especial para o verdadeiro valor de F ou complexo), existe um risco de confusão, como f n também poderia estar para o produto de n vezes de F, por exemplo, f 2 (x) = f (x) · f (x ).
(Para funções trigonométricas, geralmente esta última se destina, pelo menos para expoentes positivos. Por exemplo, em trigonometria, esta notação sobrescrito representa padrão exponenciação quando usado com funções trigonométricas : sin 2 (x) = sin (x) · sin (x). No entanto, para expoentes negativos (especialmente -1), que, no entanto, geralmente refere-se à função inversa, por exemplo, tan -1 = arctan (≠ 1 / tan).
Em alguns casos, para uma expressão em f g (x) = f r (x) pode ser derivado a partir da regra dada por g valores não inteiros de r. Isto é chamado iteração fraccionada. Um exemplo simples seria a de que, onde f é a função sucessor, f r (x) = x + r.
Funções iteradas ocorrem naturalmente no estudo dos fractais e sistemas dinâmicos.
Monoids Composição
Suponha que um tem duas (ou mais) funciona f: X → X, g: X → X que tem o mesmo domínio e intervalo. Em seguida, pode-se formar longas cadeias, potencialmente complicados destas funções compostas em conjunto, tais como o f f o g o f. Essas longas cadeias têm a estrutura algébrica de um monoid, às vezes chamado de monoid composição. Em geral, monoides composição pode ter uma estrutura extremamente complicada. Um exemplo notável é o especial curva de Rham. O conjunto de todas as funções f: X → X é chamado de semigroup transformação completa no X.
Se as funções são bijective, em seguida, o conjunto de todas as combinações possíveis destas funções formar um grupo ; e diz-se que o grupo está gerado por essas funções.
O conjunto de todos bijective funções f: X → X formam um grupo, em relação ao operador composição. Isto é o grupo simétrico, também chamado às vezes o grupo de composição.
Notação alternativa
Em meados do século 20 , alguns matemáticos decidiram que escrever "g o f" para significar "primeiro aplicar f, em seguida, aplicar g" foi muito confusa e decidiu mudar notações. Eles escreveu "xf" para "f (x)" e "XFG" para "G (f (x))". Isso pode ser mais natural e parecer mais simples do que escrever funções do lado esquerdo em algumas áreas.
Categoria Teoria usa f; g alternadamente com g o f.
Operador de composição
Dada uma função g, o operador composição 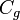 é definida como aquela operador que mapeia para funções como funções
é definida como aquela operador que mapeia para funções como funções
Operadores de composição são estudadas no campo de teoria dos operadores.