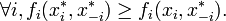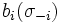Equilíbrio de Nash
Informações de fundo
Crianças SOS têm produzido uma seleção de artigos da Wikipedia para escolas desde 2005. Patrocinar uma criança para fazer uma diferença real.
| Equilíbrio de Nash | |
|---|---|
| A conceito da solução na teoria dos jogos | |
| Relacionamentos | |
| Subconjunto de | Racionabilidade, Epsilon-equilíbrio, Equilíbrio correlacionado |
| Superset de | Evolutivamente estratégia estável , Sub-jogo perfeito equilíbrio, Perfeito equilíbrio Bayesian, Mão trêmula equilíbrio perfeito |
| Significado | |
| Proposto por | John Forbes Nash |
| Usado para | Tudo jogos não-cooperativos |
| Exemplo | Dilema do prisioneiro |
Em teoria dos jogos , o equilíbrio de Nash (nomeado após John Forbes Nash, que a propôs) é uma conceito da solução de um jogo envolvendo dois ou mais jogadores, no qual nenhum jogador tem nada a ganhar com a mudando apenas a sua própria estratégia de forma unilateral. Se cada jogador optou por uma estratégia e nenhum jogador pode se beneficiar mudando sua estratégia enquanto os outros jogadores manter deles inalterada, em seguida, o conjunto atual de opções de estratégia e os pagamentos correspondentes constituem um equilíbrio de Nash.
Dito de forma simples, Amy e Bill estão em equilíbrio de Nash se Amy está fazendo a melhor decisão que pode, tendo em conta a decisão de Bill, e Bill está fazendo a melhor decisão que pode, tendo em conta a decisão de Amy. Da mesma forma, muitos jogadores estão em equilíbrio de Nash se cada um está fazendo a melhor decisão que eles podem, tendo em conta as decisões dos outros. No entanto, equilíbrio de Nash não significa necessariamente a melhor recompensa cumulativa para todos os atores envolvidos; em muitos casos, todos os jogadores podem melhorar suas recompensas se eles poderiam de alguma forma, chegar a acordo sobre estratégias diferentes a partir do equilíbrio de Nash (por exemplo, empresários concorrentes. formando uma cartel, a fim de aumentar os seus lucros).
História
O conceito de equilíbrio de Nash (NE) não é inteiramente original para Nash (por exemplo, Antoine Augustin Cournot mostrou como encontrar o que hoje chamamos o equilíbrio de Nash do Cournot jogo duopólio). Consequentemente, alguns autores se referem a ele como um "Cournot-Nash equilíbrio" (ou como um "Nash-Cournot equilíbrio"). No entanto, Nash mostrou pela primeira vez em sua dissertação, jogos não-cooperativos (1950), que Nash equilíbrios (em estratégias mistas) devem existir para todos os jogos finitos com qualquer número de jogadores. Antes do trabalho de Nash, isso só tinha sido provada para dois jogadores jogos de soma zero (por John von Neumann e Oskar Morgenstern em 1947).
Definições
Definição informal
Informalmente, um conjunto de estratégias é um equilíbrio de Nash se nenhum jogador pode fazer melhor, alterando unilateralmente a sua estratégia. Como uma heurística, pode-se imaginar que cada jogador é contada as estratégias dos outros jogadores. Se qualquer jogador gostaria de fazer algo diferente depois de ser informado sobre as estratégias dos outros, então esse conjunto de estratégias não é um equilíbrio de Nash. Se, no entanto, o jogador não quer mudar (ou é indiferente entre a mudança e não), então o conjunto de estratégias é um equilíbrio de Nash.
Isto pode ter consequências contra-intuitivas. Uma vez que o equilíbrio de Nash se concentra sobre as preferências de um indivíduo, dado que os outros mantêm suas escolhas fixo, não pode haver equilíbrio de Nash, onde, se os jogadores poderiam coordenar, todos iriam querer mudar. O caça ao veado apresenta um exemplo desse fenômeno.
Definição formal
Seja (S, f) ser um jogo, onde S é o conjunto de perfis de estratégia e f é o conjunto de perfis de recompensa. Deixar 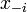 ser um perfil de estratégia de todos os jogadores, exceto para o jogador
ser um perfil de estratégia de todos os jogadores, exceto para o jogador 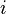 . Quando cada jogador
. Quando cada jogador 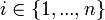 escolhe estratégia
escolhe estratégia 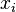 resultando em perfil estratégia
resultando em perfil estratégia 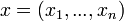 então jogador
então jogador 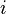 obtém retorno
obtém retorno 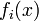 . Note-se que o retorno depende do perfil de estratégia escolhida, ou seja, sobre a estratégia escolhida pelo jogador
. Note-se que o retorno depende do perfil de estratégia escolhida, ou seja, sobre a estratégia escolhida pelo jogador 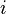 bem como as estratégias escolhidas por todos os outros jogadores. Um perfil de estratégia
bem como as estratégias escolhidas por todos os outros jogadores. Um perfil de estratégia 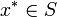 é um equilíbrio de Nash (NE) se nenhum desvio unilateral de estratégia por um único jogador é rentável, que é
é um equilíbrio de Nash (NE) se nenhum desvio unilateral de estratégia por um único jogador é rentável, que é
Um jogo pode ter uma NE estratégia pura ou um NE na sua extensão mista (que de escolher uma estratégia pura estocasticamente com um fixo frequência). Nash provou que, se permitirmos que estratégias mistas (jogadores escolhem estratégias aleatoriamente de acordo com probabilidades pré-atribuído), então cada n-jogador jogo em que cada jogador pode escolher entre um número finito de estratégias admite pelo menos um equilíbrio de Nash.
Exemplos
Jogo Competição
| Jogador 2 escolhe '0' | Jogador 2 escolhe '1' | Jogador 2 escolhe '2' | Jogador 2 escolhe '3' | |
|---|---|---|---|---|
| Jogador 1 escolhe '0' | 0, 0 | 2, -2 | 2, -2 | 2, -2 |
| Jogador 1 escolhe '1' | -2, 2 | 1, 1 | 3, -1 | 3, -1 |
| Jogador 1 escolhe '2' | -2, 2 | -1, 3 | 2, 2 | 4, 0 |
| Jogador 1 escolhe '3' | -2, 2 | -1, 3 | 0, 4 | 3, 3 |
Isto pode ser ilustrado por um jogo com dois jogadores, em que ambos os jogadores escolhem simultaneamente um número inteiro de 0 a 3 e ambos ganhar o menor dos dois pontos em números. Além disso, se um jogador escolhe um número maior que o outro, então ele / ela tem que desistir de dois pontos para o outro. Este jogo tem um equilíbrio de Nash único: ambos os jogadores escolhem a 0 (em destaque na luz vermelha). Qualquer outra escolha de estratégias pode ser melhorada se um dos jogadores reduz o seu número para um número menor do que o outro jogador. Na tabela à esquerda, por exemplo, quando se inicia no quadrado verde que é do interesse do jogador 1 de se mudar para a praça roxo, escolhendo um número menor, e que é do interesse do jogador 2 de se mudar para o quadrado azul, escolhendo um número menor. Se o jogo é modificado para que os dois jogadores ganhar o montante nomeado se ambos escolher o mesmo número, e de outra forma não ganhar nada, então há 4 Nash equilíbrios (0,0 ... 1,1 ... 2,2. ..e 3,3).
Jogo de Coordenação
| Jogador 2 adota estratégia 1 | Jogador 2 adota a estratégia 2 | |
|---|---|---|
| Jogador 1 adota estratégia 1 | A, A | B, C |
| Jogador 1 adota estratégia 2 | C, B | D, D |
O jogo é um clássico coordenação ( simétrica) de dois jogadores, dois jogo de estratégia, com o matriz de compensação mostrado para a direita, onde os retornos satisfazer A> C e D> B. Os jogadores devem, assim, coordenar, tanto em A ou em D, para receber um alto retorno. Se as escolhas dos jogadores não coincidem, uma recompensa inferior é recompensado. Um exemplo de um jogo de coordenação é o cenário onde duas tecnologias estão disponíveis para duas empresas com produtos compatíveis, e eles têm que eleger uma estratégia para se tornar o padrão do mercado. Se ambas as empresas concordam com a tecnologia escolhida, alta de vendas são esperados para ambas as empresas. Se as empresas não concordam com a tecnologia padrão, resultado poucas vendas. Ambas as estratégias são equilíbrios de Nash do jogo.
Condução em uma estrada, e ter que optar por conduzir à esquerda ou para conduzir à direita da estrada, é também um jogo de coordenação. Por exemplo, com retornos 100 significado nenhum acidente e 0 significa uma falha, o jogo de coordenação pode ser definido com a seguinte matriz de compensação:
| Conduzir à esquerda | Conduzir à direita | |
|---|---|---|
| Conduzir à esquerda | 100, 100 | 0, 0 |
| Conduzir à direita | 0, 0 | 100, 100 |
Neste caso existem dois equilíbrios de Nash de estratégia pura, quando ambos optar por conduzir à esquerda ou à direita. Se admitirmos estratégias mistas (onde uma estratégia pura é escolhida ao acaso, sujeitos a alguma probabilidade fixa), em seguida, existem três equilíbrio de Nash para o mesmo caso: dois temos visto a partir da forma pura estratégia, onde as probabilidades são (0, 100% %) de um jogador, (0%, 100%) para dois jogadores; e (100%, 0%) para um jogador, (100%, 0%) para o jogador de dois, respectivamente. Nós adicionamos outro onde as probabilidades de cada jogador é (50%, 50%).
Dilema do prisioneiro
(Mas cuidado com as diferenças na orientação da matriz de compensação)
O Dilema do Prisioneiro tem a mesma matriz de compensação, conforme ilustrado para o Jogo de Coordenação, mas agora C> A> D> B. Porque C> A e D> B, cada jogador melhora a sua situação, passando de estratégia # 1 para a estratégia # 2, não importa o que o outro jogador decide. O Dilema do Prisioneiro, portanto, tem um único Equilíbrio de Nash: ambos os jogadores escolhem a estratégia de # 2 ("traindo"). O que há muito tem feito deste um caso interessante para estudar é o fato de que D <A ("tanto trair") é globalmente inferior ao "ambos permanecem leais". A estratégia global ideal é instável; não é um equilíbrio.
Como Ian Stewart colocou, "decisões racionais, por vezes, não são sensíveis!".
Equilíbrios Nash em uma matriz de compensação
Existe uma maneira fácil de identificar numérica Nash Equilíbrio em uma Matriz de Resultados. É especialmente útil em dois jogos pessoa onde os jogadores têm mais de duas estratégias. Neste caso, a análise formal pode tornar-se demasiado longo. Esta regra não se aplica ao caso em que (estocásticos) estratégias mistas são de interesse. A regra é a seguinte: se o primeiro número de recompensa, no dupleto da célula, é o valor máximo da coluna da célula e se o segundo número é o valor máximo da linha da célula - a célula representa um equilíbrio de Nash .
Podemos aplicar esta regra para uma matriz 3x3:
| Opção A | Opção B | Opção C | |
|---|---|---|---|
| Opção A | 0, 0 | 25, 40 | 5, 10 |
| Opção B | 40, 25 | 0, 0 | 5, 15 |
| Opção C | 10, 5 | 15, 5 | 10, 10 |
Usando a regra, pode-se muito rapidamente (muito mais rapidamente do que com a análise formal) ver que as células são Equlibria Nash (B, A), (A B,), e (C, C). Com efeito, para a célula (B, A) 40 é o valor máximo da primeira coluna e 25 é o máximo da segunda fileira. Para (A, B) 25 é o máximo da segunda coluna e 40 é o valor máximo da primeira linha. Mesmo para célula (C, C). Por outras células, um ou ambos dos membros Duplet não são o máximo das linhas e colunas correspondentes.
Isto dito, a mecânica de encontrar células de equilíbrio é óbvia: encontrar o máximo de uma coluna e verifique se o segundo membro do par é o máximo da linha. Se estas condições forem satisfeitas, a célula representa um equilíbrio de Nash. Confira todas as colunas dessa forma para encontrar todas as células NE. Uma matriz NxN pode ter entre 0 e NxN estratégia puro equilíbrio de Nash.
Estabilidade
O conceito de estabilidade, útil na análise de diversos tipos de de equilíbrio, pode também ser aplicada a Nash equilíbrios.
Um equilíbrio de Nash para um jogo de estratégia mista é estável se uma pequena alteração (especificamente, uma mudança infinitesimal) em probabilidades para um jogador leva a uma situação em que duas condições são:
- o jogador que não se alterou não tem melhor estratégia na nova circunstância
- o jogador que fez a mudança agora está jogando com uma estratégia estritamente pior
Se estes casos são ambos se encontraram, em seguida, um jogador com a pequena mudança em sua estratégia mista voltará imediatamente para o equilíbrio de Nash. O equilíbrio é dito para ser estável. Se a condição não se realizar, em seguida, o equilíbrio é instável. Se apenas uma condição segura, em seguida, há uma probabilidade de haver um número infinito de estratégias ideais para o jogador que mudou. John Nash mostrou que a última situação não pode surgir numa variedade de jogos bem definidas.
No "jogo de condução" exemplo acima, existem ambos os equilíbrios estáveis e instáveis. Os equilíbrios envolvendo-estratégias mistas com 100% de probabilidades são estáveis. Se qualquer jogador muda suas probabilidades um pouco, eles vão ser tanto em desvantagem, e seu adversário não terá nenhuma razão para alterar a sua estratégia, por sua vez. O equilíbrio (50%, 50%) é instável. Se qualquer um dos jogadores muda suas probabilidades, então o outro jogador tem imediatamente uma melhor estratégia em qualquer (0%, 100%) ou (100%, 0%).
A estabilidade é crucial para aplicações práticas de equilíbrio de Nash, uma vez que o estratégia mista de cada jogador não está perfeitamente conhecido, mas tem de ser inferida a partir distribuição estatística de suas ações no jogo. Neste caso equilíbrios instáveis são muito pouco provável que ocorra na prática, uma vez que qualquer alteração de minuto nas proporções de cada estratégia visto vai levar a uma mudança de estratégia e a quebra do equilíbrio.
Note-se que a estabilidade do equilíbrio está relacionado com, mas distinto de, a estabilidade de uma estratégia.
A Coalizão à prova de Equilíbrio de Nash (CPNE) (semelhante a um forte equilíbrio de Nash) ocorre quando os jogadores não podem fazer melhor, mesmo se eles estão autorizados a comunicar e colaborar antes do jogo. Cada estratégia correlacionada suportado por dominância estrita iterated e no Fronteira de Pareto é um CPNE. Além disso, é possível para um jogo de ter um equilíbrio de Nash que é resiliente contra coalizões inferior a um tamanho especificado, k. CPNE está relacionada com a teoria do núcleo.
Ocorrência
Se um jogo tem um equilíbrio de Nash único e é jogado entre os jogadores em determinadas condições, então o conjunto NE estratégia será adoptada. Condições suficientes para garantir que o equilíbrio de Nash é jogado são:
- Os jogadores todos farão o seu melhor para maximizar o seu retorno esperado como descrito por o jogo.
- Os jogadores estão sem falhas na execução.
- Os jogadores têm inteligência suficiente para deduzir a solução.
- Não é de conhecimento comum que todos os jogadores atender a essas condições, incluindo este. Assim, não só deve cada jogador sabe os outros jogadores satisfazer as condições, mas também eles devem saber que todos eles sabem que eles encontrá-los, e sei que eles sabem que eles sabem que eles encontrá-los, e assim por diante.
Se não estiverem preenchidas as condições
Exemplos de problemas de teoria dos jogos em que estas condições não forem cumpridas:
- A primeira condição não é cumprida se o jogo não descreve corretamente as quantidades de um jogador deseja maximizar. Neste caso, não há nenhuma razão especial para esse jogador a adotar uma estratégia de equilíbrio. Por exemplo, o dilema do prisioneiro não é um dilema se um ou outro jogador tem o prazer de ser preso indefinidamente.
- Imperfeição intencional ou acidental em execução. Por exemplo, um computador com capacidade de reprodução lógica impecável de frente para um segundo computador sem falhas resultarão em equilíbrio. Introdução de imperfeição vai levar a sua interrupção seja através de perda para o jogador que comete o erro, ou por meio da negação do quarto critério "conhecimento comum" levando a possível vitória para o jogador. (Um exemplo seria um jogador de repente colocar o carro em marcha à ré no jogo da "galinha", garantindo uma perda de nenhum cenário não-win). Um exemplo notável dessa situação na ficção é a série Doctor Who Destiny of the Daleks
- Em muitos casos, a terceira condição não é satisfeita porque, mesmo que o equilíbrio tem de existir, é conhecido, devido à complexidade do jogo, por exemplo, em Xadrez chinês. Ou, se for conhecida, pode não ser conhecido por todos os jogadores, como quando se joga tic-tac-toe com uma criança pequena que quer desesperadamente para ganhar (satisfação dos outros critérios).
- O quarto critério de conhecimento comum não pode ser satisfeita mesmo se todos os jogadores que, de fato, cumprir todos os outros critérios. Jogadores indevidamente desconfiando racionalidade do outro pode adoptar contra-estratégias para o esperado jogo irracional em nome de seus oponentes. Esta é uma consideração importante em " Chicken "ou um corrida aos armamentos, por exemplo.
Se estiverem reunidas as condições
Devido às condições limitadas em que NE pode na verdade ser observados, eles são raramente tratado como um guia para o comportamento no dia-a-dia, ou observado na prática em humanos negociações. No entanto, como um conceito teórico em economia e biologia evolutiva da NE tem poder explicativo. O retorno em economia é o dinheiro, e na transmissão gene biologia evolutiva, ambos são a linha de fundo fundamental de sobrevivência. Os pesquisadores que se aplicam a teoria de jogos nesses campos afirmam que os agentes não maximizam estes por qualquer motivo será competiu fora do mercado ou do ambiente, que são atribuídas a capacidade de testar todas as estratégias. Esta conclusão é tirada da " estabilidade teoria "acima. Nestas situações, o pressuposto de que a estratégia observada é na verdade um NE tem sido muitas vezes confirmada por pesquisas.
Prova de existência
Tal como referido acima, deixe 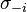 ser um perfil de estratégia mista de todos os jogadores, exceto para o jogador
ser um perfil de estratégia mista de todos os jogadores, exceto para o jogador 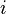 . Podemos definir um melhor resposta correspondência para o jogador
. Podemos definir um melhor resposta correspondência para o jogador 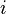 ,
, 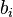 .
. 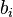 é uma relação a partir do conjunto de todas as distribuições de probabilidades sobre perfis de jogador adversário para um conjunto de jogador
é uma relação a partir do conjunto de todas as distribuições de probabilidades sobre perfis de jogador adversário para um conjunto de jogador 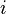 's estratégias, de tal modo que cada elemento de
's estratégias, de tal modo que cada elemento de
é uma melhor resposta a 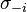 . Definir
. Definir
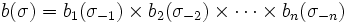 .
.
Pode-se usar o Kakutani ponto fixo teorema de provar que 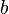 tem um ponto fixo. Isto é, há uma
tem um ponto fixo. Isto é, há uma 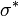 tal que
tal que 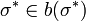 . Desde
. Desde 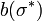 representa a melhor resposta para todos os jogadores para
representa a melhor resposta para todos os jogadores para 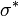 , A existência de um ponto fixo prova que existe um conjunto estratégia que é uma melhor resposta a si. Nenhum jogador pode fazer melhor, desviando, e por isso é um equilíbrio de Nash.
, A existência de um ponto fixo prova que existe um conjunto estratégia que é uma melhor resposta a si. Nenhum jogador pode fazer melhor, desviando, e por isso é um equilíbrio de Nash.
Quando Nash fez este ponto a John von Neumann em 1949, von Neumann famosa demiti-lo com as palavras: "Isso é trivial, você sabe. Isso é apenas um teorema de ponto fixo." (Veja Nasar, 1998, p. 94.)