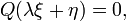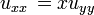Equação diferencial parcial
Você sabia ...
Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Visite o site da SOS Children at http://www.soschildren.org/
Em matemática , equações diferenciais parciais (PDE) são um tipo de equação diferencial , ou seja, um relação que envolve um desconhecido função (ou funções) de vários variáveis independentes e sua (resp.) sua derivadas parciais em relação a essas variáveis. Equações diferenciais parciais são usados para formular e, assim, ajudar a solução de, problemas envolvendo funções de várias variáveis; tais como a propagação do som ou calor , eletrostática, eletrodinâmica, o fluxo de fluido, elasticidade. Curiosamente, fenômenos físicos aparentemente distintas podem ter formulações matemáticas idênticas e, portanto, regulada pela mesma dinâmica subjacente.
Introdução
A equação diferencial parcial é relativamente simples
Esta relação implica que os valores de u (x, y) é independente de x. Daí a solução geral dessa equação é
onde f é uma função arbitrária (diferenciável) de y. O análogo equação diferencial ordinária é
que tem a solução
em que c é qualquer valor constante (independente de x). Estes dois exemplos ilustram que as soluções gerais de equações diferenciais ordinárias envolvem constantes arbitrárias, mas as soluções de equações diferenciais parciais envolvem funções arbitrárias. Uma solução de uma equação diferencial parcial não é geralmente único; condições adicionais devem ser geralmente especificado no fronteira da região onde a solução está definida. Por exemplo, no exemplo anterior, a função 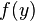 pode ser determinado se
pode ser determinado se 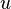 é especificado na linha
é especificado na linha 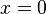 .
.
Existência e unicidade
Embora a questão da existência e unicidade de soluções de equações diferenciais ordinárias tem uma resposta muito satisfatória com a Picard-Lindelöf teorema, que está longe de ser o caso de equações diferenciais parciais. Há um teorema geral (o Teorema de Cauchy-Kovalevskaya) que indica que o Problema de Cauchy para qualquer equação diferencial parcial que é analítico na função desconhecida e seus derivados têm uma única solução analítica. Embora este resultado possa parecer para liquidar a existência e unicidade de soluções, há exemplos de equações diferenciais parciais lineares cujos coeficientes tem derivados de todas as ordens (que não são, no entanto, analítica), mas que não têm soluções em tudo: ver Lewy (1957). Mesmo se a solução de uma equação diferencial parcial existe e é único, ele pode, no entanto, ter propriedades indesejáveis.
Um exemplo de comportamento patológico é a sequência de problemas de Cauchy (dependendo n) para o Equação de Laplace
com condições iniciais
onde n é um número inteiro. O derivado de L em relação à y se aproxima de 0 uniformemente em x como n aumenta, mas a solução é
Esta solução aproxima do infinito, se nx não é um múltiplo inteiro de π para qualquer valor não-zero do y. O problema de Cauchy para a equação de Laplace é chamado de mal colocado ou não bem colocada, uma vez que a solução não depende continuamente em cima dos dados do problema. Tais problemas mal-colocados geralmente não são satisfatórios para aplicações físicas.
Notação e exemplos
No PDE, é comum para denotar derivadas parciais usando subscritos. Isto é:
Especialmente em (matemático) física, um frequentemente prefere utilização de del (que em coordenadas cartesianas é escrito 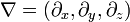 para derivadas espaciais e um ponto
para derivadas espaciais e um ponto 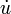 para os derivados de tempo, por exemplo, para escrever a equação de onda (ver abaixo) como
para os derivados de tempo, por exemplo, para escrever a equação de onda (ver abaixo) como
 (Notação matemática)
(Notação matemática)
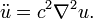 (Notação física)
(Notação física)
Equação do calor em uma dimensão espacial
A equação para a condução de calor de uma dimensão para o corpo tem a forma homogénea
onde u (t, x) é a temperatura, e α é uma constante positiva que descreve a velocidade de difusão. O problema de Cauchy para a equação consiste em especificar 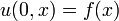 , Em que F (x) é uma função arbitrária.
, Em que F (x) é uma função arbitrária.
Soluções geral da equação de calor pode ser obtido pelo método de separação de variáveis. Alguns exemplos aparecem na artigo equação do calor. São exemplos de Série de Fourier para f periódica e Transformadas de Fourier para f não periódica. Usando a transformada de Fourier, uma solução geral da equação de calor tem a forma
onde F é uma função arbitrária. A fim de satisfazer a condição inicial, F é dado pela transformada de Fourier F, que é
Se f representa um muito pequeno, mas intensa fonte de calor, então o integral precedente pode ser aproximada pela distribuição delta, multiplicado pela força da fonte. Para obter uma fonte cuja força é normalizado para 1, o resultado é
e a solução resultante da equação de calor é
Isto é um Integral gaussiana. Pode ser avaliada para se obter
Esse resultado corresponde a uma densidade de probabilidade normal para x com média 0 e variância 2α t. A equação do calor e similares equações de difusão são ferramentas úteis para estudar os fenômenos aleatórios.
Equação de onda em uma dimensão espacial
O equação de onda é uma equação para uma função desconhecida u (t, x) da forma
Aqui u pode descrever o deslocamento de uma corda estirada de equilíbrio, ou a diferença de pressão do ar num tubo, ou a magnitude de um campo electromagnético num tubo, e c é um número que corresponde à velocidade da onda. O problema de Cauchy para a equação consiste em prescrever o deslocamento inicial e velocidade de uma corda ou outro meio:
onde f e g são dadas funções arbitrárias. A solução deste problema é dada pela A fórmula de d'Alembert:
Esta fórmula indica que a solução a (t, x) depende apenas os dados do segmento de linha inicial, que é cortado pela Curvas características
que são atraídos para trás a partir desse ponto. Estas curvas correspondem aos sinais que se propagam com a velocidade c para a frente e para trás. Por outro lado, a influência dos dados em qualquer dado ponto na linha inicial propaga com a velocidade finita c: não existe qualquer efeito fora através de um triângulo que ponto cujos lados são curvas características. Este comportamento é muito diferente da solução para a equação de calor, onde o efeito de um fonte de ponto é exibida (com pequena amplitude) instantaneamente em qualquer ponto do espaço. A solução dada acima também é válido se t é negativo, ea fórmula explícita mostra que a solução depende suavemente sobre os dados: tanto a frente e para trás problemas de Cauchy para a equação de onda estão bem colocados.
Ondas esféricas
Ondas esféricas são ondas cuja amplitude depende apenas da distância r radial a partir de um centro de fonte pontual. Para essas ondas, a equação de onda tridimensional tem a forma
Isto é equivalente a
e, portanto, a quantidade ru satisfaz a equação de onda unidimensional. Por conseguinte, uma solução geral para ondas esféricas tem a forma
em que F e G são completamente funções arbitrárias. A radiação de uma antena corresponde ao caso em que G é identicamente zero. Assim, a forma de onda transmitida a partir de uma antena tem nenhuma distorção no tempo: o único factor de distorção é de 1 / R. Esta característica de propagação de ondas sem distorções não está presente se existem duas dimensões espaciais.
Equação de Laplace, em duas dimensões
O Equação de Laplace para uma função desconhecida de duas variáveis tem a forma φ
Soluções de equação de Laplace são chamados funções harmônicas.
Conexão com funções
Soluções da equação de Laplace estão intimamente ligados com funções analíticas de uma variável complexa (aka funções holomorfas): as partes real e imaginária de qualquer função analítica são funções harmônicas conjugadas: ambos satisfazer a equação de Laplace, e seus gradientes são ortogonais. Se f = u + iv, em seguida, o Cauchy-Riemann equações de estado que
e segue-se que
Por outro lado, tendo em conta qualquer função harmónica, que é a parte real de uma função analítica, pelo menos localmente. Detalhes são fornecidos em Equação de Laplace.
Um problema típico do valor limite
Um problema típico para a equação de Laplace é encontrar uma solução que satisfaça os valores arbitrários na fronteira de um domínio. Por exemplo, nós podemos procurar uma função harmônica que assume os valores de u (θ) em um círculo de raio um. A solução foi dada por Poisson:
Petrovsky (1967, p. 248) mostra como esta fórmula pode ser obtido pela soma uma série de Fourier para φ. Se r <1, as derivadas de φ pode ser calculada através da diferenciação sob o signo integral, e pode-se verificar que φ é analítica, mesmo se u é contínuo, mas não necessariamente diferenciável. Este comportamento é típico para soluções de equações diferenciais parciais elípticas: as soluções podem ser muito mais suave do que os dados de contorno. Isto está em contraste com as soluções da equação de onda, e mais geral equações diferenciais parciais hiperbólicas, que normalmente não têm mais do que os derivados de dados.
Equação de Euler-Tricomi
O Equação de Euler-Tricomi é usado na investigação de fluxo transonic. É
Equação advecção
O equação advecção descreve o transporte de um escalar conservada 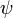 num campo de velocidades
num campo de velocidades 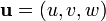 . Isto é:
. Isto é:
Se o campo de velocidade é solenoidal (isto é, 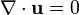 ), Então a equação pode ser simplificada para
), Então a equação pode ser simplificada para
A equação de advecção um fluxo constante dimensional 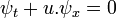 (Onde
(Onde 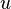 é constante) é vulgarmente referido como o problema chiqueiro. Se
é constante) é vulgarmente referido como o problema chiqueiro. Se 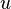 não é constante e igual
não é constante e igual 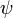 a equação é referido como Equação 'Burgers.
a equação é referido como Equação 'Burgers.
Equação Ginzburg-Landau
O Equação Ginzburg-Landau é usado em modelagem supercondutividade . É
onde 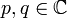 e
e 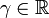 são constantes e
são constantes e 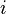 é a unidade imaginária.
é a unidade imaginária.
A equação Dym
O Dym equação é nomeado para Harry Dym e ocorre no estudo de sólitons. É
Outros exemplos
O Equação de Schrödinger é uma PDE no coração do não-relativística mecânica quântica . No WKB aproximação é a Equação de Hamilton-Jacobi.
Excepto para a equação Dym e a equação de Ginzburg-Landau, as equações acima são lineares no sentido de que eles podem ser escrito sob a forma Au = F para uma dada Um operador linear e uma dada função f. Outras equações não lineares importantes incluem as equações de Navier-Stokes que descreve o fluxo de fluidos, e Einstein equações de campo da relatividade geral .
Métodos para resolver PDE
O método de separação de variáveis trará soluções específicas de uma PDE linear em domínios muito simples, tais como retângulos que podem satisfazer as condições iniciais ou de contorno. Porque qualquer superposição de soluções de um PDE linear é novamente uma solução, as soluções específicas podem então ser combinadas para se obter soluções mais gerais. Se o domínio é finito ou periódica, uma soma infinita de soluções como uma Séries de Fourier é adequado, mas uma integral de soluções, tais como um Integral de Fourier é geralmente necessária para domínios infinitos. A solução para uma fonte pontual para a equação de calor dada acima é um exemplo da utilização de uma integral de Fourier.
Problemas de valor inicial de fronteira
Muitos problemas de Física Matemática são formulados como problemas de valor de contorno-inicial.
Vibrando cadeia
Se a cadeia de caracteres está esticada entre dois pontos em que x = 0 e x = L e L indica a amplitude do deslocamento da cadeia, então u satisfaz a equação unidimensional onda na região em que 0 <x <L e T é ilimitado . Uma vez que a cadeia é amarrado nas extremidades, u também devem satisfazer as condições de contorno
bem como as condições iniciais
O método de separação de variáveis para a equação de onda
leva a soluções de forma
onde
em que a constante k tem de ser determinado. As condições de contorno, em seguida, significa que X é um múltiplo de pecado kx, e k tem de ter a forma
onde n é um número inteiro. Cada termo na soma corresponde a um modo de vibração da corda. O modo com n = 1 é chamado de modo fundamental, e as freqüências dos outros modos são todos múltiplos de esta frequência. Eles formam a Harmônica série da cadeia, e eles são a base para a acústica musical. As condições iniciais podem então ser satisfeito através da representação de f e g como somas infinitas destes modos. Instrumentos de sopro normalmente correspondem a vibrações de uma coluna de ar com uma extremidade aberta e uma extremidade fechada. Os correspondentes condições de contorno são
O método de separação de variáveis podem também ser aplicados, neste caso, e que conduz a uma série de harmónicos impares.
O problema geral deste tipo é resolvido em Teoria de Sturm-Liouville.
Membrana vibratória
Se uma membrana é esticada sobre uma curva C que forma o limite de um domínio D no plano, as vibrações são governados pela equação de onda
se t> 0 e (x, y) é em D. A condição de contorno é 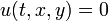 se
se 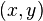 é sobre
é sobre 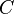 . O método de separação de variáveis leva à forma
. O método de separação de variáveis leva à forma
que por sua vez deve satisfazer
A última equação é chamado o Equação de Helmholtz. A constante k tem de ser determinado de modo a permitir um v não trivial para satisfazer a condição de contorno na C. Tais valores de k 2 são chamados os valores próprios do Laplaciano em D, e as soluções associadas são as autofunções do Laplaciano em D. A teoria de Sturm-Liouville pode ser alargado a este problema de valores próprios elíptica (Jost, 2002).
Não há geralmente métodos aplicáveis para resolver PDE não-lineares. Ainda assim, a existência e unicidade resultados (tal como o Cauchy-Kovalevskaya teorema) muitas vezes são possíveis, como são as provas de propriedades qualitativas e quantitativas importantes de soluções (obter esses resultados é uma parte importante da análise ). Solução computacional para as PDE não-linear, a Método split-step, existem para equações específicas, como a equação não-linear Schrodinger.
No entanto, algumas técnicas podem ser utilizadas para vários tipos de equações. O h-princípio é o método mais poderoso para resolver equações indeterminados. O Teoria Riquier-Janet é um método eficaz para a obtenção de informações sobre muitos analítica sistemas sobredeterminadas.
O método de características ( Método de transformação de semelhança) pode ser usada em alguns casos muito especiais para resolver equações diferenciais parciais.
Em alguns casos, uma PDE pode ser resolvido por meio de análise de perturbação em que a solução é considerada como sendo uma correcção para uma equação com uma solução conhecida. As alternativas são técnicas de análise numérica de simples esquemas de diferenças finitas para o mais maduro multigrid e métodos de elementos finitos. Muitos problemas interessantes em ciência e engenharia são resolvidos desta forma usando computadores , às vezes de alto desempenho supercomputadores.
Classificação
Algumas equações diferenciais parciais linear, de segunda ordem pode ser classificada como parabólico, hiperbólico ou elíptica. Outros, como o Equação de Euler-Tricomi têm diferentes tipos em diferentes regiões. A classificação fornece um guia para as condições iniciais e de contorno apropriadas, e lisura das soluções.
Equações de segunda ordem
Supondo 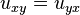 , O PDE geral de segunda ordem em duas variáveis independentes tem a forma
, O PDE geral de segunda ordem em duas variáveis independentes tem a forma
onde os coeficientes A, B, C, etc. pode depender de x e y. Esta forma é análoga à equação para uma secção cónica:
Assim como uma pessoa classifica seções cônicas em parabólico, hiperbólica, elíptica e com base no discriminante 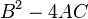 , O mesmo pode ser feito para uma PDE de segunda ordem em um determinado ponto.
, O mesmo pode ser feito para uma PDE de segunda ordem em um determinado ponto.
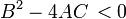 : soluções de PDEs elípticas são tão suave como os coeficientes de permitir que, no interior da região em que a equação e soluções são definidos. Por exemplo, as soluções da equação de Laplace são analíticas dentro do domínio onde são definidas, mas as soluções podem assumir valores de limite que não são suaves. O movimento de um fluido a velocidades subsónicas pode ser aproximado com PDEs elípticas, e a equação de Euler-Tricomi é elíptica em que x <0.
: soluções de PDEs elípticas são tão suave como os coeficientes de permitir que, no interior da região em que a equação e soluções são definidos. Por exemplo, as soluções da equação de Laplace são analíticas dentro do domínio onde são definidas, mas as soluções podem assumir valores de limite que não são suaves. O movimento de um fluido a velocidades subsónicas pode ser aproximado com PDEs elípticas, e a equação de Euler-Tricomi é elíptica em que x <0. 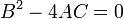 : equações que são parabólico em todos os pontos pode ser transformado numa forma análoga para a equação de calor por uma mudança de variáveis independentes. Soluções suavizar como as variáveis transformadas aumenta o tempo. A equação de Euler-Tricomi tem tipo parabólico na linha em que x = 0.
: equações que são parabólico em todos os pontos pode ser transformado numa forma análoga para a equação de calor por uma mudança de variáveis independentes. Soluções suavizar como as variáveis transformadas aumenta o tempo. A equação de Euler-Tricomi tem tipo parabólico na linha em que x = 0. 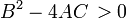 : equações hiperbólicas reter quaisquer descontinuidades de funções ou derivados nos dados iniciais. Um exemplo é a equação de onda. O movimento de um fluido a velocidades supersónicas pode ser aproximado com PDEs hiperbólicas, e a equação de Euler-Tricomi é hiperbólica em que x> 0.
: equações hiperbólicas reter quaisquer descontinuidades de funções ou derivados nos dados iniciais. Um exemplo é a equação de onda. O movimento de um fluido a velocidades supersónicas pode ser aproximado com PDEs hiperbólicas, e a equação de Euler-Tricomi é hiperbólica em que x> 0.
Se existem n variáveis independentes x 1, x 2, ..., x n, uma equação parcial geral linear diferencial de segunda ordem tem a forma
A classificação depende da assinatura dos valores próprios da matriz de coeficientes.
- Elliptic: Os autovalores são todos positivos ou todos negativos.
- Parabólico: Os autovalores são todos positivos ou todos negativos, senão um que é zero.
- Hiperbólica: Existe apenas um autovalor negativo e todo o resto são positivos, ou há apenas um autovalor positivo e todo o resto são negativos.
- Ultrahyperbolic: Existe mais do que um valor próprio positivo e mais do que um valor próprio negativa, e não existem valores próprios de zero. Há apenas teoria limitada por equações ultrahyperbolic (Courant e Hilbert, 1962).
Sistemas de equações de primeira ordem e superfícies característicos
A classificação de equações diferenciais parciais pode ser estendido para sistemas de equações de primeira ordem, em que o u é agora desconhecido com um vector m componentes, e as matrizes de coeficientes  são m por m matrizes para
são m por m matrizes para 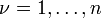 . A equação diferencial parcial assume a forma
. A equação diferencial parcial assume a forma
onde o coeficiente de matrizes A ν e o vector B pode depender x e u. Se uma hipersuperfície S é dada na forma implícita
onde φ tem uma inclinação diferente de zero, então S é uma característica de superfície para o operador G num dado ponto, se a forma característica desaparece:
A interpretação geométrica de esta condição é a seguinte: se os dados para L são prescritos sobre a superfície S, então pode ser possível determinar a derivada normal de u em S a partir da equação diferencial. Se os dados sobre a S e a equação diferencial determinar a derivada normal de u em S, então S não é característica. Se os dados sobre a S e a equação diferencial não determinam a derivada normal de u em S, em seguida, a superfície é característica, e a equação diferencial restringe os dados em S: da equação diferencial é interno ao S.
- Um sistema de primeira ordem Lu = 0 é elíptica, se nenhuma superfície é característica para L: os valores de u em S e a equação diferencial sempre determinar a derivada normal de u em S.
- Um sistema de primeira ordem é hiperbólica num ponto, se houver um espaço semelhante a superfície S com ξ normais nesse momento. Isto significa que, dado qualquer não-trivial vector η ortogonal para ξ, e um multiplicador λ escalar, a equação
m tem raízes reais λ 1, λ 2, ..., m λ. O sistema é estritamente hiperbólica se essas raízes são sempre distintos. A interpretação geométrica de esta condição é a seguinte: a forma característica Q (ζ) = 0 define um cone (cone normal) com coordenadas ζ homogénea. No caso hiperbólico, este cone tem folhas m, eo eixo ζ = λ ξ é executado dentro dessas folhas: não cruzam nenhum deles. Mas quando deslocada da origem por η, este eixo intersecta cada folha. No caso elíptica, o cone normal, não tem folhas verdadeiras.
Equações do tipo misto
Se um PDE tem coeficientes que não são constantes, é possível que ele não pertence a nenhuma destas categorias, mas sim ser do tipo misto. Um exemplo simples, mas importante é a equação de Euler-Tricomi
que é chamado elíptico-hiperbólico, porque é elíptica na região x <0, hiperbólica na região x> 0, e parabólico degenerada na linha x = 0.
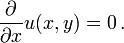
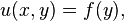
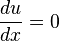
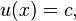
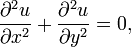
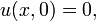
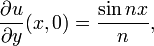
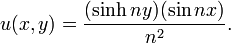
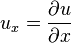
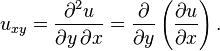
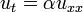
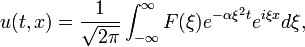
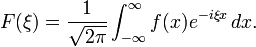

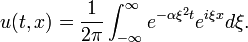

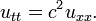
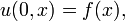

![u (t, x) = \ frac {1} {2} \ left [f (x-ct) + f (x + ct) \ right] + \ frac {1} {2-C} \ int_ {x}-ct ^ {x} + ct g (y) \, dy. \,](../../images/89/8985.png)

![u_ {tt} = c ^ 2 \ left [u_ {rr} + \ frac {2} {r} u_r \ right]. \,](../../images/89/8987.png)
![(Ru) _ {} tt = c ^ 2 \ left [(ru) _ {rr} \ right], \,](../../images/89/8988.png)
![u (t, r) = \ frac {1} {R} \ left [F (r-ct) + G (r + ct) \ right], \,](../../images/89/8989.png)
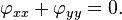
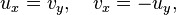

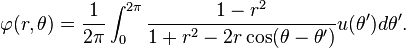
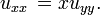
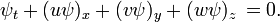

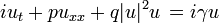
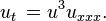

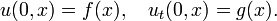
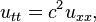
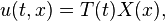
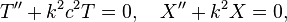
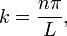
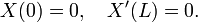
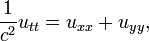
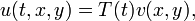
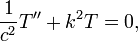
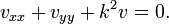
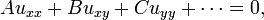
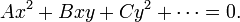
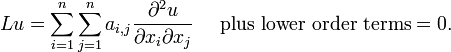
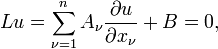

![Q \ left (\ frac {\ part \ varphi} {\ x_1 parcial}, \ ldots, \ frac {\ part \ varphi} {\ x_n parcial} \ right) = \ det \ left [\ sum _ {\ nu = 1 } ^ nA_ \ nu \ frac {\ \ varphi parcial} {\ x_ parcial \ nu} \ right] = 0. \,](../../images/90/9030.png)