Topologia

A Fita de Möbius, um objeto com apenas uma superfície e uma borda; tais formas são objeto de estudo em topologia.

Topologia ( grego topos, "lugar", e logos, "estudo") é um ramo da matemática que é uma extensão da geometria . Topologia começa com uma consideração sobre a natureza do espaço, a investigar tanto a estrutura fina e a sua estrutura global. Topologia baseia-se na teoria dos conjuntos , considerando ambos os conjuntos de pontos e famílias de conjuntos.

A palavra topologia é utilizada tanto para a área de estudo e para uma família de conjuntos com certas propriedades descritas a seguir que são utilizados para definir uma espaço topológico. De particular importância no estudo da topologia são funções ou mapas que são homeomorfismos . Informalmente, essas funções podem ser pensado como aqueles que esticar espaço sem desmanchá-lo ou aderindo partes distintas juntos.

Quando a disciplina foi primeiro adequadamente fundada, em direção ao final do século 19 , foi chamado geometria situs ( Latin geometria do lugar) e análise de situs ( Latin análise de lugar). Entre 1925 e 1975, foi uma importante área de crescimento dentro da matemática.

A topologia é um grande ramo da matemática que inclui muitos subcampos. A divisão mais básica topologia é dentro topologia de set-point, que investiga conceitos como compacidade , conectividade, e responsabilização; topologia algébrica, que investiga conceitos como homotopy e homologia; e topologia geométrica, que estuda manifolds e seus mergulhos, incluindo teoria dos nós .

Veja também: Glossário topologia para definições de alguns dos termos usados em topologia e espaço topológico para um tratamento mais técnica do assunto.

História

O Sete pontes de Königsberg é um problema famosa resolvido por Euler.

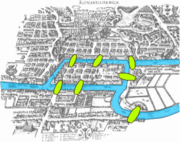
O ramo da matemática chamado agora topologia começou com a investigação de determinadas questões de geometria. Leonhard Euler 's 1736 de papel sobre Sete pontes de Königsberg é considerado como um dos primeiros resultados topológicos.

O termo "topologie" foi introduzido em alemão em 1847 por Johann Benedict Listing em Vorstudien zur Topologie, Vandenhoeck und Ruprecht, Göttingen, pp. 67, 1848. No entanto, Listing já tinha usado a palavra por dez anos na correspondência. "Topology", sua forma Inglês, foi introduzida em 1883 na revista Natureza distinguir "geometria qualitativa a partir da geometria comum em que as relações quantitativas principalmente são tratados". O termo topologista no sentido de um especialista na topologia foi usado em 1905 na revista Spectator.

Topologia moderna depende fortemente das idéias de teoria dos conjuntos , desenvolvidos por Georg Cantor na parte posterior do século 19. Cantor, além de definir para baixo as idéias básicas da teoria dos conjuntos, conjuntos de pontos considerados no espaço euclidiano , como parte de seu estudo sobre Série de Fourier.

Henri Poincaré publicado Análise Situs em 1895, introduzindo os conceitos de homotopia e homologia, que agora são considerados parte da topologia algébrica.

Maurice Fréchet, unificando o trabalho em espaços de funções de Cantor, Volterra, Arzela, Hadamard, Ascoli e outros, introduziu a espaço métrico em 1906. Um espaço métrico é agora considerado um caso especial de um espaço topológico geral. Em 1914, Felix Hausdorff cunhou o termo "espaço topológico" e deu a definição para o que hoje é chamado de Espaço Hausdorff. No uso atual, um espaço topológico é uma ligeira generalização dos espaços de Hausdorff, dada em 1922 por Kazimierz Kuratowski.

Para mais desenvolvimentos, ver topologia de set-point e topologia algébrica.

Introdução elementar

A deformação permanente ( homotopy ) de um copo de café em um donut ( toro ) e para trás.

Espaços topológicos aparecer naturalmente em quase todos os ramos da matemática. Isso fez com topologia uma das grandes ideias unificadoras da matemática. Topologia geral, ou topologia ponto-set, define e estuda as propriedades dos espaços e mapas como conectividade, compacidade e continuidade. A topologia algébrica utiliza estruturas de álgebra resumo , especialmente o grupo para estudar espaços topológicos e os mapas de entre eles.

A visão motivadora por trás de topologia é que alguns problemas geométricos não depende da forma exata dos objetos envolvidos, mas sim sobre a forma como eles estão juntos. Por exemplo, o quadrado eo círculo tem muitas propriedades em comum: ambos são objectos unidimensionais (a partir de um ponto de vista topológico) e ambos separar o plano em duas partes, a parte interna ea parte externa.

Um dos primeiros trabalhos em topologia foi a demonstração, por Leonhard Euler , que era impossível encontrar uma rota através da cidade de Königsberg (atual Kaliningrad), que iria atravessar cada uma de suas sete pontes apenas uma vez. Este resultado não depende dos comprimentos das pontes, nem sobre a sua distância uns dos outros, mas apenas em propriedades de conectividade: pontes que são conectados para que as ilhas ou margens. Este problema, o Sete pontes de Königsberg, é agora um problema famoso em matemática introdutórias, e levou ao ramo da matemática conhecido como teoria dos grafos.

Da mesma forma, o teorema bola peluda de topologia algébrica diz que "não se pode pentear o cabelo em uma bola lisa." Este fato é imediatamente convencer a maioria das pessoas, mesmo que eles podem não reconhecer a declaração mais formal do teorema, que não há não nulos contínuo vetor tangente campo na esfera . Tal como acontece com as pontes de Konigsberg, o resultado não depende de a forma exacta da esfera; aplica-se a formas de pêra e de fato qualquer tipo de blob (sujeito a certas condições sobre a lisura da superfície), contanto que ela não tem furos.

A fim de lidar com esses problemas que não dependem da forma exata dos objetos, deve ser claro sobre exatamente o que propriedades estes problemas não dependem. A partir desta necessidade surge a noção de equivalência topológica. A impossibilidade de atravessar cada ponte apenas uma vez aplica-se a todas as medidas de pontes topologicamente equivalentes aquelas em Königsberg, eo teorema bola peluda aplica-se a qualquer espaço topologicamente equivalente a uma esfera.

Intuitivamente, dois espaços são topologicamente equivalentes se uma pode ser deformada para o outro sem corte ou colagem. Uma piada tradicional é que um topologist não pode dizer a caneca de café de que ela está bebendo do filhós ela está comendo, uma vez que um donut suficientemente flexível poderia ser reformulado para a forma de um copo de café, criando uma covinha e, progressivamente, ampliando-o, ao mesmo tempo reduzindo o buraco em uma alça.

Um exercício simples é introdutório para classificar as letras minúsculas do alfabeto Inglês de acordo com a equivalência topológica. (As linhas das letras são assumidos para ter uma largura diferente de zero.) Na maior parte dos tipos de letra em utilização moderna, existe uma classe {a, b, d, e, o, p, q} de cartas com um furo, uma classe {c, f, h, k, l, m, n, r, s, t, u, v, w, x, y, z} de letras sem um buraco, e uma classe {i, j} de cartas que consiste de duas peças. g pode pertencer quer na classe com um furo, ou (em algumas fontes) pode ser o único elemento de uma classe de cartas com dois furos, dependendo de se ou não a cauda está fechado. Para um exercício mais complicado, pode-se supor que as linhas têm largura zero; pode-se obter várias classificações diferentes, dependendo de qual fonte será usada. Topologia carta é de relevância prática em stencil tipografia: O tipo de letra Braggadocio, por exemplo, pode ser cortado de um avião sem caindo aos pedaços.

Definição matemática

Seja X qualquer conjunto e seja T uma família de subconjuntos de X. Em seguida, T é uma topologia em X se

1. Tanto o conjunto vazio e X são elementos de T.
2. Qualquer união de arbitrariamente muitos elementos de T é um elemento de T.
3. Qualquer interseção de um número finito de elementos de T é um elemento de T.

Se T é uma topologia em X, X, em seguida, em conjunto com T é chamado um espaço topológico.

Todos os conjuntos em T são chamados abrir; note que, em geral, nem todos os subconjuntos de X precisa ser em T. Um subconjunto de X é dito ser fechado se o seu complemento é em T (ou seja, é aberto). Um subconjunto de X pode ser aberta, fechada, ambos, ou nenhum.

A função ou mapa de um espaço topológico para outro é chamado de contínuo se a imagem inversa de qualquer conjunto aberto é aberto. Se a função mapeia os números reais para os números reais (tanto o espaço com a topologia padrão), em seguida, esta definição de contínua é equivalente à definição de contínua no cálculo . Se uma função contínua é um-para-um e para e se o inverso da função é também contínua, então a função é chamada uma homeomorphism e o domínio da função é dito ser homeomorfos para o intervalo. Outra maneira de dizer isso é que a função tem uma extensão natural para a topologia. Se dois espaços são homeomorfos, eles têm propriedades topológicas idênticos, e são considerados topologicamente a mesma. O cubo ea esfera são homeomorphic, assim como a xícara de café eo donut. Mas o círculo não é homeomorfo ao donut.

Alguns teoremas em Topologia geral

• Cada fechado intervalo em R de comprimento finito é compacto . Mais é verdade: Em R ^n, um conjunto é compacto se e somente se é fechado e limitado. (Ver Teorema de Heine-Borel).
• Cada imagem contínua de um espaço compacto é compacto.
• Teorema de Tychonoff: A (arbitrária) produtos de espaços compactos é compacto.
• Um subespaço compacto de um espaço de Hausdorff é fechado.
• Cada seqüência de pontos em um espaço métrico compacto tem uma subseqüência convergente.
• Cada intervalo em que R é ligado.
• A imagem contínua de um conexidade está conectado.
• A espaço métrico é Hausdorff, também normal e paracompact.
• O teoremas metrization fornecer condições necessárias e suficientes para uma topologia de vir de um métrica.
• O Tietze extensão teorema: Em um espaço normal, cada função real contínua definida em um subespaço fechado pode ser estendido para uma aplicação contínua definido em todo o espaço.
• O Baire categoria teorema: Se X é um completar espaço métrico ou um espaço localmente compacto Hausdorff, em seguida, o interior de cada união de countably muitos nenhum lugar conjuntos densos está vazio.
• Em um paracompact espaço Hausdorff cada tampa aberta admite um partição de unidade subordinada à tampa.
• Cada conectados à caminho, localmente conectado à caminho e semi-localmente espaço simplesmente ligado tem um cobertura universal.

Topologia geral também tem algumas surpreendentes conexões para outras áreas da matemática. Por exemplo:

• na teoria dos números, A prova de Furstenberg da infinitude dos números primos.

Algumas noções úteis de topologia algébrica

Veja também lista de tópicos topologia algébrica.

• Homologia e cohomology: Números de Betti, Euler característicos .
• Intuitivamente-aplicações atraentes: Brouwer teorema de ponto fixo, Teorema bola peluda, Borsuk-Ulam, Ham teorema sanduíche.
• Homotopia grupos (incluindo o grupo fundamental).
• As classes de Chern, Aulas de Stiefel-Whitney, Classes de Pontryagin.

Generalizações

Ocasionalmente, é preciso usar as ferramentas da topologia, mas um "conjunto de pontos" não está disponível. Em uma topologia pointless considera, em vez do treliça de conjuntos abertos como a noção básica da teoria, enquanto Topologias Grothendieck são certas estruturas definido no arbitrária categorias que permitem a definição de roldanas nas categorias, e com que a definição de teorias muito gerais cohomology.