Infinito

Assuntos Relacionados: Matemática

Você sabia ...

Crianças SOS voluntários ajudaram a escolher artigos e fez outros materiais currículo SOS mães cada um cuidar de uma família de crianças apadrinhadas .

O símbolo do infinito, ∞, em vários tipos de letra.

Infinito (simbolicamente representado com ∞) vem dos latino- Infinitas ou "ilimitação." Refere-se a vários conceitos distintos (geralmente ligados à idéia de "sem fim"), que surgem em filosofia , matemática , e teologia.

Em matemática , "infinito" é frequentemente utilizado em contextos onde ela é tratada como se fosse um número (ou seja, conta ou medidas coisas: "um número infinito de termos"), mas é um tipo diferente de "número" do que o números reais . Infinito está relacionada com os limites , números de Aleph, aulas de teoria dos conjuntos , Conjuntos Dedekind-infinito, grandes cardeais, O paradoxo de Russell, aritmética não-padrão, números hiperreais, geometria projetiva, números reais estendidos ea absoluto Infinito.

História

Os primeiros pontos de vista indígenas do infinito

O Isha Upanishad do Yajurveda (c. 4º para o século 3 aC) afirma que "se você remover uma parte do infinito ou adicionar uma parte para o infinito, ainda que permanece é infinito".

Purnam Adah purnam idam (Isto é completo, este está cheio)

udacyate pūrṇāt purnam (Do total, o total é subtraído)

pūrṇasya purnam Adaya (Quando a cheio é retirado do total)

evāvasiṣyate purnam (O total ainda permanecerá.) - Isha Upanishad

O índio matemático texto Surya Prajnapti (c. 400 aC) classifica todos os números em três conjuntos: enumeráveis, inúmeros e infinitos. Cada uma delas foi subdividido em três ordens:

Enumerable: mais baixo, intermediário e alto
Inumeráveis: quase inumeráveis, realmente inúmeras e inúmeras innumerably
Infinito: quase infinita, verdadeiramente infinito, infinitamente infinita

O Jainistas foram os primeiros a descartar a idéia de que todos os infinitos eram os mesmos ou igual. Eles reconheceram diferentes tipos de infinidades infinitas: de comprimento (um dimensão), infinito em área (duas dimensões), infinito em volume (três dimensões), e infinito perpetuamente (número infinito de dimensões).

De acordo com Singh (1987), Joseph (2000) e Agrawal (2000), o maior número enumerable N dos jainistas corresponde ao conceito moderno de aleph-nulo 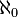$\ Aleph_0$ (O número cardinal do conjunto infinito de números inteiros 1, 2, ...), a menor cardinal número transfinito. O jainistas também definiu todo um sistema de números cardinais infinitos, dos quais o maior número enumerable N é o menor.

No trabalho Jaina na teoria dos conjuntos , dois tipos básicos de números infinitos são distinguidas. Em ambos físico e fundamentos ontológicos, foi feita uma distinção entre asaṃkhyāta ("incontáveis, inumeráveis") e ananta ("infinito, ilimitado"), entre rigidamente delimitada e vagamente infinidades limitadas.

Lógica

Na lógica de um argumento regressão infinita é "um tipo distintivamente filosófica do argumento pretendendo mostrar que uma tese é defeituoso porque gera uma série infinita quando quer (formulário A) não existe tal série ou (formulário B) foram que ela exista, a tese não teria a papel (por exemplo, da justificação) que é suposto para jogar ".

Símbolo da infinidade

John Wallis apresenta o símbolo do infinito à literatura matemática.

A origem precisa do símbolo do infinito "∞" não é clara. Uma possibilidade é sugerido pelo nome às vezes é chamado-o lemniscate, a partir do lemniscus latim, que significa "fita". Pode-se imaginar andando sempre ao longo de um loop simples formado a partir de uma fita.

Uma explicação popular é que o símbolo infinito é derivada a partir da forma de um Fita de Möbius. Mais uma vez, pode-se imaginar andando ao longo da sua superfície para sempre. No entanto, esta explicação é improvável, uma vez que o símbolo tinha sido usado para representar o infinito por mais de 200 anos antes August Ferdinand Möbius e Johann Benedict Listing descobriu a fita de Möbius em 1858 .

Também é possível que ele é inspirado mais velha religiosa / alquímico simbolismo. Por exemplo, verificou-se em tibetanos balançar esculturas, eo ouroboros, ou infinito cobra, é muitas vezes representado nesta forma.

John Wallis é geralmente creditado com a introdução ∞ como um símbolo do infinito em 1655 em seu De sectionibus conicis. Uma conjectura sobre por que ele escolheu este símbolo é que ele derivou-lo a partir de um número romano para 1000 que por sua vez foi derivado do Numeral etrusca de 1000, que parecia um pouco como CIƆ e às vezes era usada para significar "muitos". Outra conjectura é que ele derivou-lo da letra grega ω ( omega), a última letra do alfabeto grego .

Outra possibilidade é que o símbolo foi escolhido porque era mais fácil de girar uma personalidade "8" por 90 ° quando diagramação foi feito à mão. O símbolo é às vezes chamado de "preguiçoso oito", evocando a imagem de um "8" deitado de lado.

Outra crença popular é que o símbolo do infinito é uma descrição clara do ampulheta virou 90 °. Obviamente, essa ação faria com que o vidro da hora de tomar o tempo infinito para esvaziar apresentando, portanto, um exemplo tangível de infinito. A invenção da ampulheta é anterior à existência do símbolo do infinito permitindo que essa teoria seja plausível.

O símbolo infinito é representado em Unicode pelo ∞ personagem (U + 221E).

Infinito matemático

Infinito é usado em vários ramos da matemática.

Cálculo

Em análise real, o símbolo 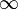$\ Infty$ , Chamado "infinito", denota uma ilimitada limite . $x \ rightarrow \ infty$ significa que x cresce sem limites, e $x \ rightarrow - \ infty$ significa o valor de x está diminuindo sem limites. Se f (t) ≥ 0 para cada t, então

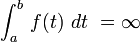$\ Int_ {a} ^ {b} \, f (t) \ dt \ = \ infty$ significa que f (t) não ligada uma área finita a partir de uma ab
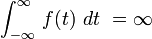$\ Int _ {- \ infty} ^ {\ infty} \, f (t) \ dt \ = \ infty$ significa que a área sob o f (t) é infinito.
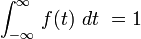$\ Int _ {- \ infty} ^ {\ infty} \, f (t) \ dt \ = 1$ significa que a área sob o f (t) é igual a 1

Infinito também é usado para descrever infinita série:

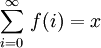$\ sum_ {i = 0} ^ {\ infty} \, f (i) = x$ significa que a soma da série infinita converge para algum valor real x.
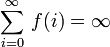$\ Sum_ {i = 0} ^ {\ infty} \, f (i) = \ infty$ significa que a soma da série infinita diverge no sentido específico que as somas parciais crescer sem limites.

Propriedades algébricas

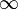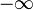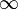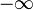Infinito é muitas vezes usado, não só para definir um limite, mas como um valor no sistema número real affinely estendida. Pontos rotulada $\ Infty$ e $- \ Infty$ podem ser adicionados ao espaço topológico dos números reais, produzindo os dois pontos compactification dos números reais. Adicionando propriedades algébricas para isso nos dá os números reais estendidos. Nós também podemos tratar $\ Infty$ e $- \ Infty$ quanto ao mesmo, o que conduz a um ponto- compactificação dos números reais, que é a reta projetiva real. Geometria projetiva também introduz uma linha no infinito em geometria plana , e assim por diante para dimensões superiores.

A linha de número real estendido adiciona dois elementos chamados infinito ( 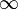$\ Infty$ ), Maior do que todos os outros números reais estendidos, e infinito negativo ( 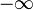$- \ Infty$ ), Menos do que todos os outros números reais estendidos, para os quais algumas operações aritméticas podem ser executadas.

Análise Complexa

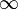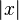Como na análise real, em análise complexa o símbolo $\ Infty$ , Chamado "infinito", denota uma ilimitada limite . $x \ rightarrow \ infty$ significa que a magnitude $| X |$ de x cresce para além de qualquer valor atribuído. A ponto marcado 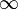$\ Infty$ podem ser adicionados ao plano complexo como um espaço topológico dando a-ponto um compactificação do plano complexo. Quando isto é feito, o espaço resultante é um unidimensional colector de complexo, ou Riemann superfície , o chamado plano complexo estendido ou o Esfera de Riemann. As operações aritméticas semelhantes às apresentadas abaixo para os números reais estendido também pode ser definida, no entanto não há nenhuma distinção entre os sinais (é, por conseguinte, uma infinidade excepção de que não pode ser adicionado a si mesmo). Por outro lado, este tipo de borda infinita permite a divisão por zero, ou seja, 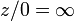$Z / 0 = \ infty$ para qualquer número complexo z. Neste contexto, é muitas vezes útil considerar meromorfas funções como mapas para a esfera de Riemann tendo o valor de 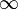$\ Infty$ nos pólos. O domínio de uma função de valor complexo pode ser estendido para incluir o ponto no infinito bem. Um exemplo importante de tais funções é o grupo de Transformações de Möbius.

Análise fora do padrão

A formulação original do cálculo por Newton e Leibniz usadas quantidades infinitesimais. No século XX, foi demonstrado que este tratamento poderia ser colocado em um fundamento rigoroso através de vários sistemas lógicos, incluindo análise infinitesimal suave e análise fora do padrão. Neste último, infinitesimais são inversíveis, e seus inversos são números infinitos. Os infinitos neste sentido são parte de um todo campo; não há equivalência entre eles como com o cantoriana transfinites. Por exemplo, se H é um número infinito, em seguida, H + H = 2H e H + são diferentes um número infinito.

Teoria de conjuntos

Um tipo diferente de "infinito" são o ordinais e cardinais infinitos da teoria dos conjuntos. Georg Cantor desenvolveu um sistema de números transfinitos, em que o primeiro cardeal transfinite é aleph-nulo 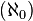$(\ Aleph_0)$ , O cardinalidade do conjunto de números naturais . Essa concepção matemática moderna do infinito quantitativo desenvolvido no final do século XIX do trabalho por Cantor, Gottlob Frege, Richard Dedekind e outros, usando a idéia de coleções, ou conjuntos.

A abordagem de Dedekind foi essencialmente a adotar a idéia de um-para-um correspondência como um padrão para comparação do tamanho dos conjuntos, e para rejeitar a vista de Galileu (que derivou de Euclides ) que o conjunto não pode ser do mesmo tamanho que a parte. Um conjunto infinito pode ser simplesmente definido como tendo o mesmo tamanho que, pelo menos, um dos seus " adequadas "partes; esta noção de infinito é chamado Dedekind infinito.

Cantor definiu dois tipos de números infinitos, os números ordinais e da números cardinais. Os números ordinais podem ser identificados com conjuntos bem-ordenada, ou contagem exercida a qualquer ponto de parada, incluindo pontos, depois de um número infinito já foram contadas. Generalizando finito eo infinito ordinária sequências que são mapas dos positivos inteiros leva a mapeamentos de números ordinais, e sequências transfinitos. Os números cardinais definir o tamanho dos conjuntos, ou seja, quantos membros eles contêm, e pode ser padronizada, escolhendo o primeiro número ordinal de um determinado tamanho para representar o número cardinal de que tamanho. O menor ordinal infinito é o dos números inteiros positivos, e qualquer conjunto que tem o cardinality dos números inteiros é infinito contável. Se um conjunto é muito grande para ser colocado em correspondência um a um com os números inteiros positivos, ele é chamado incontável. vistas de Cantor prevaleceu ea Matemática moderna aceita infinito real. Certos prolongados Número sistemas, como o números hiperreais, incorporar os números ordinários (finitos) e um número infinito de diferentes tamanhos.

Nossa intuição adquirida com conjuntos finitos quebra quando se lida com conjuntos infinitos. Um exemplo disto é a O paradoxo de Hilbert do Grand Hotel.

Cardinalidade do contínuo

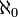Um dos resultados mais importantes de Cantor foi que a cardinalidade do continuum ( $\ Mathbf c$ ) É maior do que a dos números naturais ( ${\ Aleph_0}$ ); ou seja, há um número mais real do que R números naturais N. Nomeadamente, Cantor mostrou que $\ Mathbf {c} = 2 ^ {\ aleph_0}> {\ aleph_0}$ (Veja Argumento diagonal de Cantor).

O hipótese do contínuo indica que não há nenhum número cardinal entre a cardinalidade dos reais eo cardinality dos números naturais, isto é, 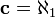$\ Mathbf {c} = \ aleph_1$ . No entanto, esta hipótese não pode nem ser provada nem refutada dentro do amplamente aceito Zermelo-Fraenkel, mesmo supondo que o Axioma da Escolha.

Cardinal aritmética podem ser usados para mostrar que não apenas o número de pontos numa A linha número real é igual ao número de pontos em qualquer segmento de linha que, mas que esta é igual ao número de pontos do plano e, na verdade, em qualquer espaço de dimensão finita. Estes resultados são altamente contra-intuitiva, uma vez que implica que existem sub-grupos apropriados de um conjunto infinito S que têm o mesmo tamanho como S.

O primeiro destes resultados é evidente, considerando, por exemplo, a tangente função, que fornece um um-para-um entre o intervalo [-0.5π, 0.5π] e R (ver também O paradoxo de Hilbert do Grand Hotel). O segundo resultado foi provado por Cantor em 1878, mas só se tornou intuitivamente evidente em 1890, quando Giuseppe Peano apresentou o curvas de preenchimento do espaço, linhas curvas que torcer e virar o suficiente para preencher a totalidade de qualquer quadrado ou cubo, ou hypercube, ou espaço de dimensão finita. Estas curvas podem ser utilizadas para definir um um-para-um entre os pontos no lado de um quadrado e aqueles na praça.

Também é possível demonstrar que conjuntos com cardinalidade estritamente maior que $\ Mathbf c$ existir. Eles incluem, por exemplo:

o conjunto de todos os subconjuntos de R, ou seja, o conjunto de R poder, escrito P (R) ou 2 ^R
o conjunto R ^R de todas as funções a partir de R R

Ambos têm cardinalidade 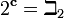$2 ^ \ mathbf {c} = \ beth_2$ (Veja Número Beth).

Matemática sem o infinito

Leopold Kronecker rejeitou a noção de infinito e começou uma escola de pensamento, no filosofia da matemática chamado finitismo que influenciou a escola filosófica e matemática de construtivismo matemático.

Infinidade física

Em física , aproximações de números reais são usados para medições contínuas e números naturais são usados para medições discretas (isto é, a contagem). É, portanto, assumido por físicos que não quantidade mensurável pode ter um valor infinito, por exemplo, tendo um valor infinito em um sistema de número real estendido (veja também: número hiper-real), ou exigindo a contagem de um número infinito de eventos. É por exemplo presume impossível para qualquer corpo para ter massa infinita ou energia infinita. Não existe o conceito de entidades infinitos (tais como um infinito onda plana), mas não há meios de produção de tais coisas.

Deve ser salientado que esta prática de recusar valores infinitos para quantidades mensuráveis não vem de a priori ou motivações ideológicas, mas sim a partir de motivações mais metodológicas e pragmáticas. Uma das necessidades de qualquer teoria científica e física é dar fórmulas utilizáveis que correspondem a ou, pelo menos, aproximada da realidade. Como um exemplo, se qualquer objecto de massa gravitacional infinita existisse, qualquer utilização da fórmula para calcular a força gravitacional conduziria a um resultado infinito, o que seria de nenhum benefício uma vez que o resultado seria sempre a mesma, independentemente da posição e a massa do outro objecto. A fórmula seria útil nem para calcular a força entre dois objetos de massa finito nem para calcular seus movimentos. Se um objeto de massa infinita existisse, qualquer objeto de massa finita seriam atraídos com força infinita (e, portanto, aceleração) pelo objeto massa infinita, o que não é o que podemos observar na realidade.

Este ponto de vista não significa que o infinito não pode ser usado na física. Por amor, cálculos, equações, teorias e aproximações de conveniência, muitas vezes usar séries infinitas, ilimitadas funções , etc., e podem envolver quantidades infinitas. Os físicos, contudo, exigir que o resultado final ser fisicamente significativa. Em teoria quântica de campo infinitos surgem que precisam ser interpretados de tal forma a conduzir a um resultado fisicamente significativa, um processo chamado renormalização . Uma aplicação em que surgem infinitos é a quantificação de temperaturas termodinâmicas .

No entanto, existem algumas circunstâncias atualmente aceitas onde o resultado final é o infinito. Um exemplo é buracos negros . Os físicos têm verificado que, quando uma estrela experiências colapso gravitacional, ele acabará por encolher a um ponto de tamanho zero, e, portanto, têm densidade infinita. Este é um exemplo do que é chamado uma singularidade matemática, ou um ponto onde as leis da matemática, da física e, portanto, quebrar. Alguns físicos acreditam agora que a singularidade pode ser fisicamente real, e, desde então, voltaram sua atenção para encontrar novas matemática onde infinitos são possíveis.

Infinito em cosmologia

Uma questão intrigante é se o infinito real existe no nosso físico universo : Existem infinitas estrelas? Será que o universo tem de volume infinito? O espaço "continuar para sempre"? Esta é uma questão importante de aberto cosmologia . Note-se que a questão do ser infinito é logicamente separada da questão de não ter fronteiras. A superfície bidimensional da Terra, por exemplo, é finito, ainda não tem uma borda. Ao caminhar / vela / condução reta longa o suficiente, você vai voltar para o local exato que você começou. O universo, pelo menos em princípio, pode ter um semelhante topologia ; se você voar com sua nave espacial para a frente o tempo suficiente, talvez você acabaria por rever o seu ponto de partida. Se, no entanto, o universo está em constante expansão , então você nunca poderia voltar ao seu ponto de partida, mesmo em uma escala de tempo infinito.

Representações de computador do infinito

O IEEE padrão de ponto flutuante especifica valores positivos e negativos infinito; estes podem ser o resultado de estouro aritmético, divisão por zero, ou outras operações excepcionais.

Algumas linguagens de programação (por exemplo, J e UNIDADE) especificar maior e menos elementos, ou seja, comparar valores que (respectivamente) maior do que ou menor do que todos os outros valores. Estes também podem ser denominadas superior e inferior, ou mais infinito e menos infinito; eles são úteis como valores sentinela em algoritmos que envolvem triagem, pesquisar ou janelamento. Em idiomas que não tem maiores e menos elementos, mas não permitem sobrecarga de operadores relacionais, é possível criar maiores e menos elementos (com alguns em cima, e o risco de incompatibilidade entre as implementações).

Perspectiva e pontos no infinito nas artes

Artwork perspectiva utiliza o conceito de imaginário pontos de fuga, ou pontos no infinito, localizado a uma distância infinita do observador. Isso permite que artistas para criar pinturas que 'realista' retratam distância e encurtamento de objetos. Artista MC Escher é especificamente conhecido por empregar o conceito de infinito em sua obra nesta e em outras maneiras.

Retirado de " http://en.wikipedia.org/w/index.php?title=Infinity&oldid=198896642 "