
Energia cinética
Sobre este escolas selecção Wikipedia
Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas de todo o mundo. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança

A energia cinética de um objeto é o extra de energia que possui devido ao seu movimento. É definido como o trabalho necessário para acelerar uma massa de uma dada massa de descanso para a sua velocidade de corrente. Tendo ganhado essa energia durante a sua aceleração , o corpo mantém essa energia cinética, a menos que suas mudanças de velocidade. Trabalho negativo da mesma magnitude iria ser obrigado a retornar o corpo a um estado de repouso do que a velocidade.
Etimologia
| Procurar cinética em Wiktionary, o dicionário livre. |
O adjetivo "cinética" ao substantivo energia tem suas raízes no Grego palavra para "motion" ( kinesis). Os termos de energia cinética e de trabalho e seus significados presentes científicos datam de meados do século 19. Entendimentos iniciais dessas idéias pode ser atribuído a Gaspard-Gustave Coriolis, que em 1829 publicou o artigo intitulado Du Calcul de l'Effet des Machines esboçando a matemática da energia cinética.
William Thomson , mais tarde Lord Kelvin, é dado o crédito por cunhar o termo energia cinética c. 1849.
Introdução
Existem várias formas de energia: energia química, calor , radiação electromagnética , energia potencial (gravitacional, eléctrico, elástica, etc.), energia nuclear, energia de repouso. Estes podem ser classificados em duas classes principais: energia potencial e energia cinética.
A energia cinética pode ser melhor compreendida pelos exemplos que demonstram como é transformada a partir de outras formas de energia e para as outras formas. Por exemplo, um ciclista irá usar energia química que foi fornecida pelo alimento para acelerar uma bicicleta para uma velocidade escolhida. Esta velocidade pode ser mantida sem mais trabalho, excepto para superar a resistência do ar e o atrito. A energia foi convertida em energia de movimento, conhecido como energia cinética mas o processo não é completamente eficiente e também calor é produzido dentro do ciclista.
A energia cinética do movimento da bicicleta e do ciclista pode ser convertido em outras formas. Por exemplo, o ciclista pode encontrar um monte apenas o suficiente para costa, de modo que a bicicleta vem a uma parada completa na parte superior. A energia cinética já em grande parte foi convertida em energia potencial gravitacional que pode ser lançado pela roda livre para o outro lado da colina. (Desde a bicicleta perdeu alguma da sua energia ao atrito, ele nunca vai recuperar toda a sua velocidade sem mais pedalar. Note-se que a energia não é perdida porque só foi convertida a outra forma por fricção.) Como alternativa, o ciclista pode conectar um dínamo de uma das rodas e também gerar alguma energia eléctrica na descida. A bicicleta estaria viajando mais lentamente na parte inferior do morro, porque parte da energia foi desviado para tornar a energia elétrica. Outra possibilidade seria para o ciclista para aplicar os travões, caso em que a energia cinética seria dissipada, por atrito, como a energia de calor.
Como qualquer quantidade física que é uma função da velocidade, a energia cinética de um objecto não depende apenas da natureza interior do referido objecto. Ele também depende da relação entre o objeto eo observador (na física um observador é formalmente definido por uma classe particular de sistema de coordenadas chamado de referencial inercial). Grandezas físicas como este estão a ser dito não invariável. A energia cinética é co-localizado com o objeto e contribui para o seu campo gravitacional.
Cálculos
Existem várias equações diferentes que podem ser utilizados para calcular a energia cinética de um objecto. Em muitos casos, eles dão quase a mesma resposta para dentro precisão bem mensurável. Onde elas diferem, a escolha de qual a utilização é determinada pela velocidade do corpo ou o seu tamanho. Assim, se o objecto está em movimento, a uma velocidade muito menor do que a velocidade da luz, os newtonianos mecânica (clássica) será suficientemente precisa; mas, se a velocidade é comparável à velocidade da luz, relatividade começa a fazer diferenças significativas para o resultado e deve ser usado. Se o tamanho do objecto é sub-atómico, a mecânica quântica equação é mais adequado.
Energia cinética newtoniana
A energia cinética de corpos rígidos
Em mecânica clássica , a energia cinética de um "objeto de ponto" (um corpo tão pequeno que o seu tamanho pode ser ignorada), ou um não rotativa corpo rígido, é dada pela equação 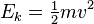 em que m é a massa e v é a velocidade do corpo.
em que m é a massa e v é a velocidade do corpo.
Por exemplo - seria de calcular a energia cinética de uma viagem de massa 80 kg a 18 metros por segundo (40 mph) como 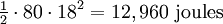 .
.
Note-se que a energia cinética aumenta com o quadrado da velocidade. Isto significa, por exemplo, que se você estiver viajando duas vezes mais rápido, você terá quatro vezes mais energia cinética. Como resultado disto, um carro viaja duas vezes mais rápido necessita de quatro vezes a maior distância para parar (assumindo que uma força de travagem constante. Ver trabalho mecânico ).
Assim, a energia cinética pode ser calculada utilizando a fórmula:
onde:
- E k é a energia cinética em joules
- m é a massa em quilogramas, e
- v é a velocidade em metros por segundo.
Para a energia cinética de translação de um corpo com constante de massa m, cujo centro de massa está se movendo em linha reta com velocidade v, como visto acima é igual a
onde:
- m é a massa do corpo
- v é a velocidade do centro de massa do corpo.
Assim, a energia cinética é uma medida relativa e nenhum objecto pode ser dito ter uma energia cinética única. Um motor de foguete pode ser vista a transferir a sua energia para o navio do foguete ou a corrente de escape, dependendo do quadro de referência escolhido. Mas a energia total do sistema, ou seja, a energia cinética, a energia química combustível, energia térmica, etc., serão conservados independentemente da escolha do quadro de medição.
A energia cinética de um objecto está relacionada com o seu impulso pela equação:
Derivação e definição
O trabalho feito acelerar uma partícula durante o intervalo de tempo infinitesimal dt é dado pelo produto escalar da força e de deslocamento:
Aplicando a regra do produto, vemos que:
Portanto (assumindo uma massa constante), o seguinte pode ser visto:
Como este é um diferencial total (ou seja, ele só depende do estado final, não como a partícula got), podemos integrá-lo e chamar o resultado de energia cinética:
Esta equação indica que a energia cinética (E k) é igual ao integrante do produto escalar da velocidade (v) de um corpo e o alteração ínfima do corpo de impulso (p). Supõe-se que o corpo começa com nenhuma energia cinética quando está em repouso (parado).
A energia cinética dos sistemas
Para um único ponto, ou um corpo rígido que não está a rodar, a energia cinética vai para zero, quando o corpo pára.
No entanto, para os sistemas que contenham vários corpos em movimento de forma independente, que podem exercer forças entre si, e pode (ou não pode) ser rotativa; isso não é mais verdade.
Esta energia é chamado de 'energia interna ".
A energia cinética do sistema, a qualquer instante no tempo é simplesmente a soma das energias cinéticas da masses- incluindo a energia cinética devido às rotações.
Um exemplo seria o sistema solar. No centro de massa do sistema solar, o Sol está (quase) estacionária, mas os planetas e planetóides estão em movimento sobre o assunto. Assim, mesmo em uma estacionária centro de massa, ainda está presente energia cinética.
No entanto, recalculando a energia a partir de quadros diferentes seria tedioso, mas há um truque. A energia cinética do sistema a partir de um sistema inercial diferente pode ser simplesmente calculado a partir da soma da energia cinética no centro de massa e adicionando a energia em que a massa total dos organismos no centro de massa teria se fosse mover-se a velocidade relativa entre as duas armações.
Isto pode ser simplesmente mostrado: Seja v a velocidade relativa da trama k do centro de massa de i:
No entanto, deixe- 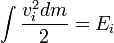 a energia cinética no centro de massa,
a energia cinética no centro de massa, 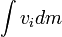 seria simplesmente o momento total que é, por definição, zero no centro de massa, e deixe a massa total:
seria simplesmente o momento total que é, por definição, zero no centro de massa, e deixe a massa total: 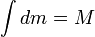 . Substituindo, obtém-se:
. Substituindo, obtém-se:
A energia cinética de um sistema depende, assim, o inercial de referência e é mais baixo em relação ao centro de massa quadro de referência, isto é, num quadro de referência no qual o centro de massa é estacionária. Em qualquer outro ponto de referência não é uma energia cinética adicional correspondente à massa total em movimento com a velocidade do centro de massa.
Corpos girando
Se um corpo rígido está a rodar sobre qualquer linha através do centro de massa, em seguida, tem energia cinética de rotação ( 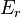 ), Que é simplesmente a soma das energias cinéticas das suas partes móveis, e portanto, é igual a:
), Que é simplesmente a soma das energias cinéticas das suas partes móveis, e portanto, é igual a:
onde:
- ω é o corpo da velocidade angular .
- r é a distância de qualquer dm massa a partir dessa linha
- I é o corpo de momento de inércia
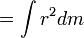
(Nesta equação o momento de inércia deve ser feita sobre um eixo que passa pelo centro de massa e de rotação medido por ω deve ser em torno desse eixo; existir mais equações gerais para sistemas em que o objecto é sujeita a oscilar devido à sua forma excêntrica) .
Rotação em sistemas
Por vezes, é conveniente dividir a energia cinética total de um corpo em a soma do centro de massa do corpo de energia cinética de translação e a energia de rotação em torno do centro de massa energia rotacional:
onde:
- E k é a energia cinética total
- Et é a energia cinética de translação
- E r é a energia de rotação ou energia cinética angular no quadro de repouso
Assim, a energia cinética de uma bola de ténis em voo é a energia cinética devido à sua rotação, mais a energia cinética devido à sua tradução.
Energia cinética relativística de corpos rígidos
Na relatividade especial , temos de mudar a expressão para momento linear. Integrando por partes, obtemos:
Lembrando que 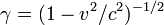 , Temos:
, Temos:
E assim:
A constante de integração é encontrada por meio da observação de que 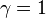 quando
quando 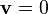 , Então temos a fórmula habitual:
, Então temos a fórmula habitual:
Se a velocidade de um corpo é uma fração significativa da velocidade da luz , é necessário o uso de mecânica relativista (a teoria da relatividade como exposto por Albert Einstein ) para calcular a sua energia cinética.
Para um objecto relativista o momento p é igual a:
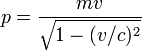 ,
,
em que m é a massa de repouso, v é a velocidade do objeto, e c é a velocidade da luz no vácuo.
Assim, o trabalho despendido acelerar um objeto a partir do repouso a uma velocidade relativista é:
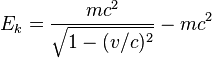 .
.
A equação mostra que a energia de um objecto se aproxima do infinito, como a velocidade v se aproxima da velocidade da luz c, assim, não é possível acelerar um objecto através deste limite.
O subproduto matemática deste cálculo é a fórmula de equivalência massa-energia do corpo em repouso deve ter conteúdo de energia igual a:
A uma velocidade baixa (v <
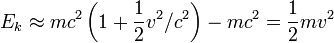 ,
,
Então, o total de energia E pode ser dividida em a energia da massa de repouso mais a energia cinética newtoniana tradicional a baixas velocidades.
Quando objetos se movem a uma velocidade muito mais lenta do que a luz (por exemplo, fenômenos cotidianos da Terra), os dois primeiros termos da série predominam. O termo seguinte na aproximação é pequeno para baixas velocidades, e pode ser encontrado através da extensão da expansão em série de Taylor por mais um termo:
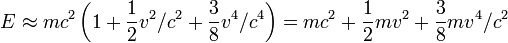 .
.
Por exemplo, para uma velocidade de 10 km / s a correcção para a energia cinética Newtoniano é de 0,07 J / kg (em energia cinética newtoniano de 50 MJ / kg) e para uma velocidade de 100 km / s é de 710 J / kg (em energia cinética newtoniano de 5 GJ / kg), etc.
Para velocidades mais altas, a fórmula para a energia cinética relativística é derivado simplesmente subtraindo a energia massa de repouso do total de energia:
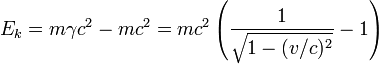 .
.
A relação entre a energia cinética e impulso é mais complicado, neste caso, e é dado pela equação:
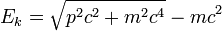 .
.
Isto também pode ser expandido como uma série de Taylor , o primeiro termo que representa a expressão simples de mecânica de Newton.
O que isso sugere é que as fórmulas para a energia e impulso não são especiais e axiomática, mas sim conceitos que emergem a partir da equação de massa com energia e os princípios da relatividade.
Energia cinética mecânica quântica de corpos rígidos
No reino da mecânica quântica, o valor esperado da energia cinética do elétron, 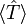 , Para um sistema de electrões descrito pela wavefunction
, Para um sistema de electrões descrito pela wavefunction  é uma soma de 1-elétron valores esperados operador:
é uma soma de 1-elétron valores esperados operador:
onde 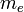 é a massa do elétron e
é a massa do elétron e 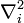 é o Atuação operador Laplaciano sobre as coordenadas do i th elétron eo somatório é executado sobre todos os elétrons. Observe que esta é a versão quantizada da expressão não-relativista para a energia cinética em termos de impulso:
é o Atuação operador Laplaciano sobre as coordenadas do i th elétron eo somatório é executado sobre todos os elétrons. Observe que esta é a versão quantizada da expressão não-relativista para a energia cinética em termos de impulso:
O densidade funcional formalismo da mecânica quântica exige o conhecimento da densidade eletrônica única, ou seja, formalmente não requer conhecimento da função de onda. Dada uma densidade de elétrons 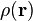 , Exatamente o N-elétron energia cinética funcional é desconhecido; no entanto, para o caso específico de um sistema 1 de electrões, a energia cinética pode ser escrito como
, Exatamente o N-elétron energia cinética funcional é desconhecido; no entanto, para o caso específico de um sistema 1 de electrões, a energia cinética pode ser escrito como
onde ![T [\ rho]](../../images/173/17351.png) É conhecido que a energia cinética Von Weizsàcker funcional.
É conhecido que a energia cinética Von Weizsàcker funcional.
Alguns exemplos
Uso nave espacial energia química para decolar e ganhar energia cinética considerável para chegar velocidade orbital. Esta energia cinética adquirida durante o lançamento permanecerá constante enquanto em órbita, porque não há quase nenhum atrito. No entanto, torna-se aparente a re-entrada quando a energia cinética é convertida em calor.
A energia cinética pode ser passada de um objeto para outro. No jogo de bilhar, o jogador dá energia cinética para a bola golpeando-o com o taco. Se a bola se choca com outra bola, ele vai abrandar drasticamente ea bola colidiu com a vontade de acelerar a uma velocidade como a energia cinética é passada para ele. Colisões em bilhar são efetivamente colisões elásticas, onde a energia cinética é preservada.
Volantes está a ser desenvolvido como um método de armazenamento de energia (ver artigo armazenamento de energia do volante). Isto ilustra que a energia cinética de rotação também pode ser. Observe a fórmula nos artigos sobre volantes para o cálculo da energia cinética de rotação é diferente, embora análogo.
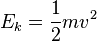
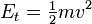
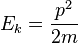
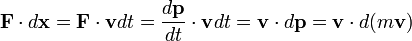
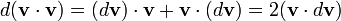
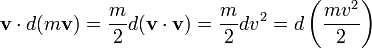
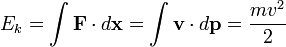
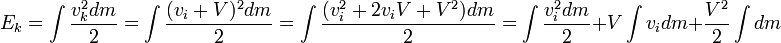

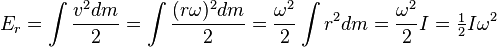
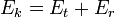
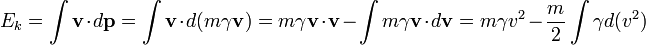
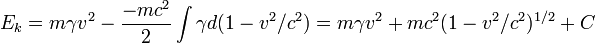

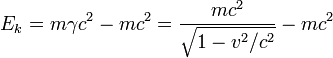
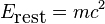
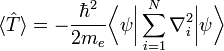
![T [\ rho] = \ frac {1} {8} \ int \ frac {\ nabla \ rho (\ mathbf {r}) \ cdot \ nabla \ rho (\ mathbf {r})} {\ rho (\ mathbf {R})} d ^ 3r](../../images/173/17350.png)
