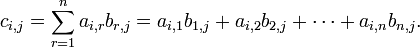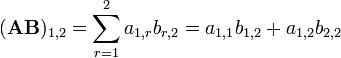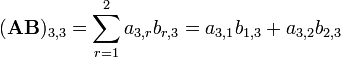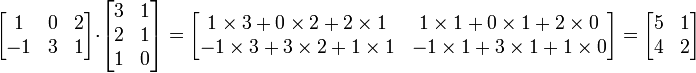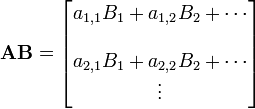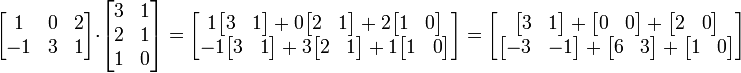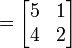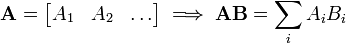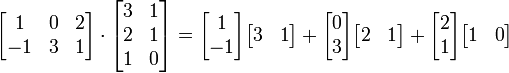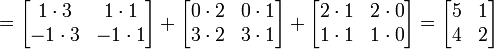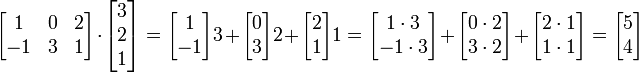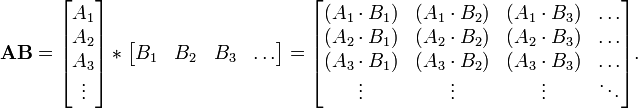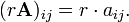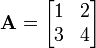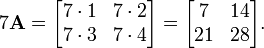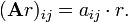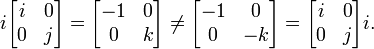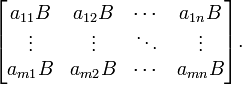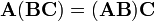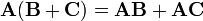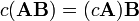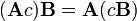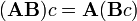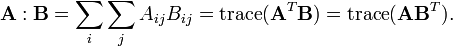A multiplicação de matrizes

Assuntos Relacionados: Matemática

Você sabia ...

Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/

Em matemática , a multiplicação de matrizes é a operação de multiplicação de uma matriz com qualquer um escalar ou outra matriz. Este artigo dá uma visão geral das várias formas de executar a multiplicação de matrizes.

Produto de matriz comum

Esta é a forma mais frequentemente utilizado e mais importante para multiplicar as matrizes. Ela é definida entre duas matrizes apenas se o número de colunas da primeira matriz é o mesmo que o número de linhas da segunda matriz. Se A é uma matriz m -by- N e B é um N -by- p matriz, em seguida, o seu produto é uma matriz de m -by- p denotado por AB (ou, por vezes, A · B). Se C = AB, e c _{i, j representa} a entrada em C na posição (i, j), então

$c_ {i, j} = \ sum_ {r = 1} ^ n a_ {i, r} b_ {r, j} = {i a_, b_ 1} {1, j} + a_ {i, 2} {b_ 2, j} + \ cdots + a_ {i, n} b_ {n, j}.$

para cada par i e j com 1 ≤ i ≤ M e 1 ≤ j ≤ p. O sistema algébrico de " unidades matriciais "resume as propriedades abstratas deste tipo de multiplicação.

Calculando diretamente da definição

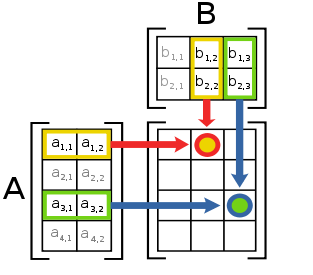
A imagem da esquerda mostra como calcular a (1,2) e o elemento (3,3) elemento de AB, se A é uma matriz 4 x 2, e B é uma matriz de 2 x 3. Os elementos de cada matriz são emparelhados na direcção das setas; cada par é multiplicado, e os produtos são adicionados. A localização do número resultante em AB corresponde a linha e coluna que foram consideradas.

$(\ Mathbf {AB}) _ {1,2} = \ sum_ {r = 1} ^ 2 a_ {1, r} B_ {r, 2} = {1,1} a_ b_ {1,2} + a_ {1,2} {2,2} b_$

$(\ Mathbf {AB}) _ {} 3,3 = \ sum_ {r = 1} ^ 2 a_ {3, r} B_ {r, 3} = {3,1} a_ b_ {1,3} + a_ {3,2} {2,3} b_$

Por exemplo:

$\ Begin {} bmatrix 1 & 2 0 e -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 & 2 \\ \\ 1 1 0 & \ end {bmatrix} = \ begin {} bmatrix 1 \ vezes 3 + 0 \ times 2 + 2 \ times 1 & 1 \ times 1 + 0 \ times 1 + 2 \ times 0 \\ -1 \ times 3 + 3 \ times 2 + 1 \ times 1 & -1 \ times \ 1 + 3 vezes 1 + 1 \ times 0 \ end {bmatrix} = \ begin {} bmatrix 5 & 1 & 2 4 \\ \ end {bmatrix}$

O método de coeficientes vectores

Esta multiplicação de matrizes também pode ser considerada a partir de um ponto de vista um pouco diferente: ele adiciona vetores juntos depois de ser multiplicado por diferentes coeficientes. Se A e B são matrizes dada por:

$\ Mathbf {A} = \ begin {} bmatrix a_ {1,1} e a_ {1,2} & \ \\ pontos a_ {2,1} e {2,2} a_ \ & pontos \\ \ vdots & \ vdots & \ ddots \ end {bmatrix}$ e $\ Mathbf {B} = \ begin {} bmatrix b_ {1,1} e b_ {1,2} & \ \\ pontos b_ {2,1} e {2,2} b_ & \ pontos \\ \ vdots & \ vdots & \ ddots \ end {bmatrix} = \ begin {} bmatrix B_1 \\ B_2 \\ \ vdots \ end {bmatrix}$

em seguida

$\ Mathbf {AB} = \ begin {} bmatrix a_ {1,1} B_1 + a_ {1,2} B_2 + \ cdots \\\\ a_ {2,1} B_1 + a_ {2,2} B_2 + \ cdots \\ \ vdots \ end {bmatrix}$

O exemplo revisitado:

$\ Begin {} bmatrix 1 & 2 0 e -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 & 2 \\ \\ 1 1 0 & \ end {bmatrix} = \ begin {} bmatrix 1 \ begin {} bmatrix 3 e 1 \ end {bmatrix} + 0 \ begin {} bmatrix 2 e 1 \ end {bmatrix} + 2 \ begin {} bmatrix 1 & 0 \ end {} \\ bmatrix -1 \ begin {} bmatrix 3 e 1 \ end {bmatrix} + 3 \ begin {} bmatrix 2 e 1 \ end {bmatrix} + 1 \ begin {} bmatrix 1 & 0 \ end {bmatrix} \ end {bmatrix} = \ begin {bmatrix} \ begin {} bmatrix 3 e 1 \ end {bmatrix} + \ begin {bmatrix} 0 & 0 \ end {bmatrix} + \ begin {} bmatrix 2 & 0 \ end {bmatrix} \\ \ begin {bmatrix} -3 e -1 \ end {bmatrix} + \ begin {} bmatrix 6 e 3 \ end {bmatrix} + \ begin {} bmatrix 1 & 0 \ end {bmatrix} \ end {bmatrix}$

$= \ Begin {} bmatrix 5 & 1 & 2 4 \\ \ end {bmatrix}$

As linhas na matriz à esquerda são a lista de coeficientes. A matriz da direita é a lista de vetores. No exemplo, a primeira linha é [1 0 2], e, assim, assumir um vezes o primeiro vector, 0 vezes o segundo vector, e 2 vezes o terceiro vector.

A equação pode ser ainda mais simplificado através da utilização produtos exteriores:

$\ Mathbf {A} = \ begin {} bmatrix A_1 & A_2 & \ dots \ end {bmatrix} \ implica \ mathbf {AB} = \ sum_i A_iB_i$

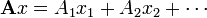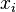Os termos desta soma são matrizes da mesma forma, cada um descrevendo o efeito de uma coluna de A e B de uma linha no resultado. As colunas de A pode ser visto como um sistema de coordenadas da transformação, ou seja, dado um vetor x que têm $\ mathbf {A} = x + A_1x_1 A_2x_2 + \ cdots$ onde $x_i$ são coordenadas ao longo do 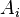$A_i$ "Eixos". Os termos 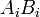$A_iB_i$ são como 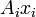$A_ix_i$ , Com excepção de que 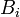$B_i$ contém o i-ésimo de coordenadas para cada vector de coluna B, cada um dos quais é independentemente transformado em paralelo.

O exemplo revisitado:

$\ Begin {} bmatrix 1 & 2 0 e -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 & 2 \\ \\ 1 1 0 & \ end {bmatrix} = \ begin {} bmatrix 1 -1 \\ \ end {bmatrix} \ begin {} bmatrix 3 e 1 \ end {bmatrix} + \ begin {} bmatrix 0 \\ três \ end {bmatrix} \ begin {} bmatrix 2 & 1 \ end {bmatrix} + \ begin {} bmatrix 2 \\ 1 \ end {bmatrix} \ begin {} bmatrix 1 & 0 \ end {bmatrix}$

$= \ Begin {} bmatrix 1 \ cdot 3 e 1 \ cdot 1 -1 \\ \ cdot 3 e -1 \ cdot 1 \ end {bmatrix} + \ begin {} bmatrix 0 \ cdot 2 & 0 \ cdot 1 \\ 3 \ cdot 2 e 3 \ cdot 1 \ end {bmatrix} + \ begin {} bmatrix 2 \ cdot 1 & 2 \ cdot 0 1 \\ \ cdot 1 & 1 \ cdot 0 \ end {bmatrix} = \ begin {bmatrix } 5 & 1 & 2 4 \\ \ end {bmatrix}$

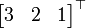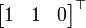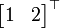Os vectores $\ Begin {} bmatrix 3 & 2 & 1 \ end {bmatrix} ^ \ topo$ e $\ Begin {} bmatrix 1 & 1 & 0 \ end {bmatrix} ^ \ topo$ foram transformados para $\ Begin {} bmatrix 5 e 4 \ end {bmatrix} ^ \ topo$ e $\ Begin {} bmatrix 1 & 2 \ end {bmatrix} ^ \ topo$ em paralelo. Pode-se também transformá-los um por um com os mesmos passos:

$\ Begin {} bmatrix 1 & 2 0 e -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 \\ \\ 2 1 \ end {bmatrix} = \ begin {} bmatrix 1 \ \ -1 \ end {} bmatrix 3+ \ begin {} bmatrix 0 \\ três \ end {} bmatrix 2+ \ begin {} bmatrix 2 \\ 1 \ end {} bmatrix 1 = \ begin {} bmatrix 1 \ cdot 3 -1 \\ \ cdot 3 \ end {bmatrix} + \ begin {} bmatrix 0 \ cdot 2 3 \\ \ cdot 2 \ end {bmatrix} + \ begin {} bmatrix 2 \ cdot 1 \\ 1 \ cdot 1 \ end {bmatrix} = \ begin {} bmatrix 5 4 \\ \ end {bmatrix}$

Método Vector-listas

O produto de matriz comum pode ser pensado como um de um produto escalar coluna da lista de vetores e um linha-lista de vetores. Se A e B são matrizes dada por:

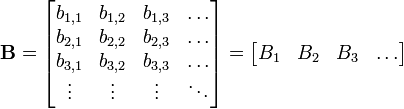
$\ Mathbf {A} = \ begin {} bmatrix a_ {1,1} e a_ {1,2} e a_ {1,3} & \ \\ pontos a_ {2,1} e {2,2} a_ & A_ {2,3} e \ \\ pontos a_ {3,1} e {3,2} a_ & a_ {3,3} & \ pontos \\ \ vdots & \ vdots & \ vdots & \ ddots \ end { bmatrix} = \ begin {} bmatrix A_1 \\ \\ A_2 A_3 \\ \ vdots \ end {bmatrix}$ e $\ Mathbf {B} = \ begin {} bmatrix b_ {1,1} e b_ {1,2} e b_ {1,3} & \ \\ pontos b_ {2,1} e {2,2} b_ & b_ {2,3} & \ \\ pontos b_ {3,1} e {3,2} b_ & b_ {3,3} & \ pontos \\ \ vdots & \ vdots & \ vdots & \ ddots \ end { bmatrix} = \ begin {} bmatrix B_1 & B_2 & B_3 & \ dots \ end {bmatrix}$

onde

Um ₁ é o vector da linha de todos os elementos de uma forma _1, A _{2 x} é o vector da linha de todos os elementos de uma forma _{2, x,} etc,

e B é _um vector de todos os elementos da forma b _{x coluna, 1} B ₂ é o vector de todos os elementos da forma b _{x, 2,} etc. coluna,

em seguida

$\ Mathbf {AB} = \ begin {} bmatrix A_1 \\ \\ A_2 A_3 \\ \ vdots \ end {} * bmatrix \ begin {} bmatrix B_1 & B_2 & B_3 & \ dots \ end {bmatrix} = \ begin { bmatrix} (a_1 \ cdot B_1) e (a_1 \ cdot B_2) e (a_1 \ cdot B_3) & \ \\ pontos (a_2 \ cdot B_1) e (A_2 \ cdot B_2) e (A_2 \ cdot B_3) & \ dots \\ (A_3 \ cdot B_1) e (A_3 \ cdot B_2) e (A_3 \ cdot B_3) & \ pontos \\ \ vdots & \ vdots & \ vdots & \ ddots \ end {} bmatrix.$

Propriedades

A multiplicação de matrizes não é comutativa (isto é, AB ≠ BA), exceto em casos especiais. É fácil perceber porquê: você não pode esperar para mudar as proporções com os vetores e obter o mesmo resultado. Também é fácil ver como a ordem dos factores determina o resultado quando se sabe que o número de colunas da matriz de proporções tem de ser o mesmo que o número de linhas na matriz de vectores: eles têm que representam o mesmo número de vetores.

Embora a multiplicação de matrizes não é comutativa, os determinantes de AB e BA são sempre iguais (se A e B são matrizes quadradas de mesmo tamanho). Veja o artigo sobre determinantes para uma explicação. No entanto multiplicação de matrizes é comutativa quando ambas as matrizes são diagonal e da mesma dimensão.

Esta noção de multiplicação é importante porque, se A e B são interpretados como transformações lineares (que é feito quase universalmente), em seguida, o produto de matrizes AB corresponde à composição das duas transformações lineares, com B a ser aplicado em primeiro lugar.

Além disso, todas as noções de multiplicação de matrizes descritas aqui compartilham um conjunto de propriedades comuns descritos abaixo.

Algoritmos

O complexidade da multiplicação de matrizes, se realizada, ingenuamente, é O (n ³), mas algoritmos mais eficientes que existem. Algoritmo de Strassen, concebido por Volker Strassen em 1969 e muitas vezes referida como "a multiplicação de matrizes rápido", baseia-se em uma forma inteligente de multiplicar duas matrizes de 2 × 2, que requer apenas 7 multiplicações (em vez da habitual 8). Aplicando este truque de forma recursiva dá um algoritmo com um custo de 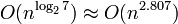$O (n ^ {\ log_ {2}} 7) \ approx O (n ^ {2,807})$ . Na prática, porém, é raramente utilizado, uma vez que é difícil de implementar e que carece estabilidade numérica. O fator constante implícita na notação O grande é de cerca de 4.695.

O algoritmo com o expoente mais baixa conhecida, que foi apresentado pelo Don Coppersmith e Shmuel Winograd em 1990 , tem uma complexidade assintótica de O (n ^2.376). É semelhante ao algoritmo de Strassen: uma maneira inteligente é concebido para multiplicar dois k × k matrizes com menos de multiplicações ³ k, e esta técnica é aplicada de forma recursiva. Ele melhora no fator constante em algoritmo de Strassen, reduzindo-o a 4,537. No entanto, o termo constante implícita no O (n ^2.376) resultado é tão grande que o algoritmo de Coppersmith-Winograd só vale a pena para matrizes que são grandes demais para lidar em computadores de hoje (Knuth, 1998).

Uma vez que qualquer algoritmo para multiplicar duas matrizes n × n tem de processar todos os 2 × n ² entrada, há um limite inferior de assintótica Ω (n) ² operações. Raz (2002) revela um limite inferior de 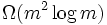$\ Omega (m ^ 2 \ log M)$ para circuitos delimitados coeficiente aritméticas sobre os números reais ou complexos.

Cohn et al. (2003, 2005) colocar métodos, como os algoritmos de Strassen e Coppersmith-Winograd in, um completamente diferente do grupo teórico de contexto. Eles mostram que, se famílias de produtos grinalda de Abelian com grupos simétricos que satisfaçam determinadas condições existe, algoritmos de multiplicação de matrizes com complexidade quadrática essencial existir. A maioria dos pesquisadores acredita que este é realmente o caso (Robinson, 2005).

Multiplicação escalar

A multiplicação escalar de uma matriz A = _(aij) e um escalar r r dá um produto A do mesmo tamanho que um. As entradas de r A são dados pela

$(R \ mathbf {A}) _ {ij} = r \ cdot a_ {ij}. \,$

Por exemplo, se

$\ Mathbf {A} = \ begin {} bmatrix 1 & 2 \\ 3 e 4 \ end {bmatrix}$

em seguida

$7 \ mathbf {A} = \ begin {} bmatrix 7 \ cdot 1 e 7 \ cdot 2 \\ 7 \ cdot 3 e 7 \ cdot 4 \ end {bmatrix} = \ begin {} bmatrix 7 e 14 \\ 21 & 28 \ end {} bmatrix.$

Se estamos preocupados com matrizes mais de um anel, então a multiplicação acima é, por vezes, chamado de multiplicação enquanto a multiplicação esquerda para a direita é definido como sendo

$(\ Mathbf {A} r) _ {ij} = a_ {ij} \ cdot r. \,$

Quando o anel é subjacente conmutativo , por exemplo, o campo de número real ou complexa, as duas multiplicações são os mesmos. No entanto, se o anel não é conmutativo, tais como o quatérnions, eles podem ser diferentes. Por exemplo

$i \ begin {bmatrix} i & 0 \\ 0 & j \\ \ end {bmatrix} = \ begin {bmatrix} -1 e 0 \\ 0 & k \\ \ end {bmatrix} \ ne \ begin {bmatrix} -1 e 0 \\ 0 & -k \\ \ end {bmatrix} = \ begin {bmatrix} i & 0 \\ 0 & j \\ \ end {bmatrix} i.$

Produto Hadamard

Para duas matrizes com as mesmas dimensões, que tem o produto de Hadamard, também conhecido como o produto entrywise e o produto de Schur. Ele pode ser generalizada para reter não só para matrizes, mas também para os operadores. O Produto de Hadamard de dois m -by- n matrizes A e B, indicadas por A • B, m é um n -by- matriz dada por (A • B) _ij = a _{ij ij} b. Por exemplo

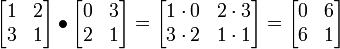$\ Begin {} bmatrix 1 & 2 & 3 1 \\ \\ \ end {bmatrix} \ bala \ begin {} bmatrix 0 e 3 \\ 2 e 1 \\ \ end {bmatrix} = \ begin {} bmatrix 1 \ cdot 0 e 2 \ cdot 3 3 \\ \ cdot 2 e 1 \ cdot 1 \\ \ end {bmatrix} = \ begin {bmatrix} 0 & 6 \\ 6 & 1 \\ \ end {bmatrix}$ .

Note-se que o produto é um Hadamard submatriz do produto de Kronecker (ver abaixo).

O produto Hadamard é comutativa .

O produto Hadamard é estudada pelos teóricos da matriz, e aparece em algoritmos de compressão com perdas, como JPEG, mas é praticamente intocado pelo algebristas lineares. Discutem-se em (Horn e Johnson, 1994, cap. 5).

Produto de Kronecker

Para quaisquer duas matrizes arbitrárias A e B, temos o produto directo ou Um produto de Kronecker ⊗ B definido como

$\ Begin {} bmatrix a_ {11} B & a_ {12} B & \ cdots & a_ {} 1n B \\ \ vdots & \ vdots & \ ddots & \ \\ vdots a_ {} m1 B & a_ {m2} B & \ cdots & a_ {} mn B \ end {} bmatrix.$

Observe que, se A é m -by- n e B é p r -by- então A ⊗ B é um p.f. -by- nr matriz. Novamente, isto não é multiplicação comutativa.

Por exemplo

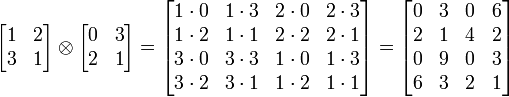$\ Begin {} bmatrix 1 & 2 & 3 1 \\ \\ \ end {bmatrix} \ otimes \ begin {} bmatrix 0 e 3 \\ 2 e 1 \\ \ end {bmatrix} = \ begin {} bmatrix 1 \ cdot 0 e 1 \ cdot 3 & 2 \ cdot 0 e 2 \ cdot 3 \\ 1 \ cdot 2 e 1 \ cdot 1 & 2 \ cdot 2 & 2 \ cdot 1 \\ 3 \ cdot 0 e 3 \ cdot 3 & 1 \ cdot 0 e 1 \ cdot 3 3 \\ \ cdot 2 e 3 \ cdot 1 & 1 \ cdot 2 e 1 \ cdot 1 \\ \ end {bmatrix} = \ begin {bmatrix} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 6 & 3 \\ 3 & 2 & 1 \ final {} bmatrix$ .

Se A e B representam transformações lineares V ₁ → W ₁ e V ₂ → W _2, respectivamente, então A ⊗ B representa o produto tensor dos dois mapas, V ₁ ⊗ V ₂ → W ₁ ⊗ W _2.

As propriedades comuns

O Wikibook O Livro de Provas matemáticas tem uma página sobre o tema de: As provas de propriedades de matrizes

Todas as três noções de multiplicação de matrizes são associativa :

$\ \ Mathbf {A} (\ mathbf {BC}) = (\ mathbf {AB}) \ mathbf {C}$

e distributiva:

$\ \ Mathbf {A} (\ mathbf {B} + \ mathbf {C}) = \ mathbf {AB} + \ mathbf {AC}$

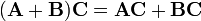$\ (\ Mathbf {A} + \ mathbf {B}) \ mathbf {C} = \ mathbf {AC} + \ mathbf {BC}$ .

e compatível com multiplicação escalar:

$\ C (\ mathbf {AB}) = (c \ mathbf {A}) \ mathbf {B}$

$\ (\ Mathbf {A} c) \ mathbf {B} = \ mathbf {A} (c \ mathbf {B})$

$\ (\ Mathbf {AB}) c = \ mathbf {A} (\ mathbf {B} c)$

Note-se que estes três pares separados de expressões irá ser iguais uns aos outros apenas se a multiplicação e adição no campo escalar são conmutativo, isto é, o campo escalar é um anel conmutativo. Veja multiplicação escalar acima de um contra-exemplo, como o campo escalar de quaternions.

Produto interno Frobenius

O produto interno Frobenius, às vezes denotado A: B é o produto interno-componente sábio de duas matrizes como se eles são vetores. Em outras palavras, é a soma das entradas do produto de Hadamard, isto é,

$\ Mathbf {A}: \ mathbf {B} = \ sum_i \ sum_j A_ {ij} B_ {ij} = \ operatorname} {trace (\ mathbf {A} ^ T \ mathbf {B}) = \ operatorname {trace} (\ mathbf {A} \ mathbf {B} ^ T).$

Este produto interno induz a Frobenius norma.

Retirado de " http://en.wikipedia.org/w/index.php?title=Matrix_multiplication&oldid=203157436 "