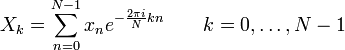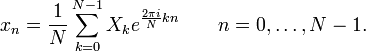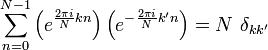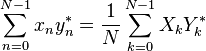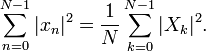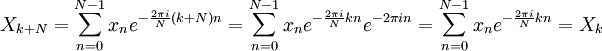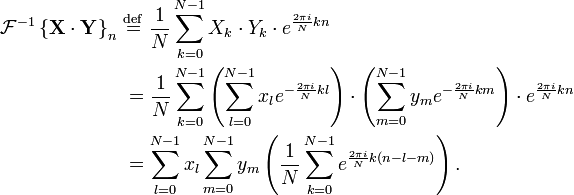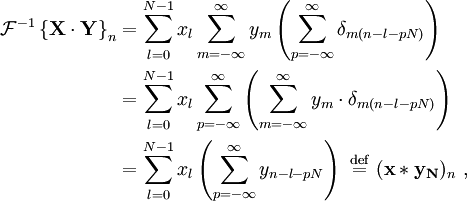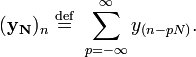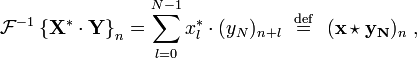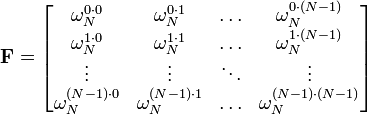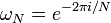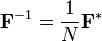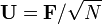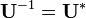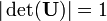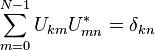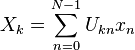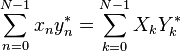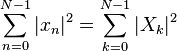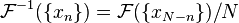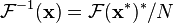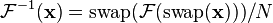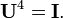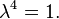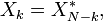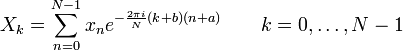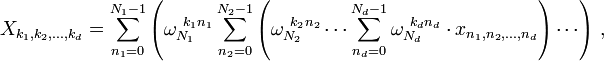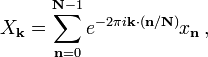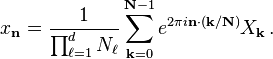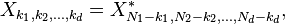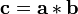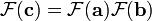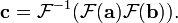Transformada de Fourier discreta
Fundo para as escolas Wikipédia
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Patrocinar uma criança para fazer uma diferença real.
| Transformadas de Fourier |
|---|
| Transformada de Fourier contínua |
| Séries de Fourier |
| De tempo discreto transformada de Fourier |
| Transformada de Fourier discreta |
Em matemática , a transformada de Fourier discreta (DFT) é uma das formas específicas de A análise de Fourier. Como tal, ele transforma uma função para outra, o que é chamado a representação do domínio de frequência, ou simplesmente o DFT, da função original (que é muitas vezes uma função no domínio do tempo). Mas o DFT requer uma função de entrada que é valores discretos e cuja diferente de zero tem uma duração limitada (finito). Tais entradas são muitas vezes criados por amostragem de uma função contínua, como a voz de uma pessoa. E, ao contrário do de tempo discreto transformada de Fourier (DTFT), que avalia apenas componentes de frequência suficientes para reconstruir o segmento finito que foi analisada. Sua transformação inversa não pode reproduzir todo o domínio do tempo, a menos que a entrada passa a ser periódica (para sempre). Por isso, muitas vezes é dito que o DFT é uma transformação para análise de Fourier finita-domínio funções de tempo discreto. As funções de base sinusoidais da decomposição tem as mesmas propriedades.
Uma vez que a função de entrada é uma sequência finita de reais ou números complexos , o DFT é ideal para processamento de informações armazenadas em computadores . Em particular, a DFT é amplamente empregado em processamento de sinal e áreas afins para analisar as frequências contidas em uma amostra sinalizar, para resolver equações diferenciais parciais , e para realizar outras operações como circunvoluções. O DFT pode ser calculado de forma eficiente, na prática, usando um Fast Fourier Transform (FFT).
Uma vez que os algoritmos de FFT são comumente empregues para calcular o DFT, os dois termos são utilizados intermutavelmente em configurações coloquial, embora existe uma distinção clara: "DFT" refere-se a uma transformação matemática, independentemente da forma como é calculado, enquanto "FFT" refere-se a qualquer um dos vários algoritmos eficientes para a TFD. Esta distinção é ainda mais turva, no entanto, pelo sinónimo Transformada de Fourier finita para o DFT, que, aparentemente, antecede o termo "transformação rápida de Fourier" (Cooley et ai., 1969), mas tem a mesma initialism.
Definição
A sequência de N números complexos x 0, ..., N-1 x é transformada na sequência de números complexos n x 0, ..., N-1 X pelo DFT de acordo com a fórmula:
onde 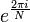 é um enésimo primitivo raiz da unidade.
é um enésimo primitivo raiz da unidade.
A transformação é, por vezes, representado pelo símbolo 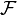 , Como em
, Como em 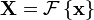 ou
ou  ou
ou 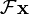 .
.
A Fourier discreta inversa (IDFT) é dada por
Uma simples descrição destas equações é que os números complexos 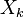 representam a amplitude e fase dos diferentes componentes sinusoidais do "sinal" de entrada
representam a amplitude e fase dos diferentes componentes sinusoidais do "sinal" de entrada 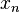 . O DFT calcula o
. O DFT calcula o 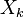 do
do 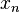 , Enquanto a IDFT mostra como calcular a
, Enquanto a IDFT mostra como calcular a 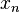 como uma soma de componentes senoidais
como uma soma de componentes senoidais 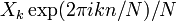 com freqüência
com freqüência 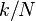 ciclos por amostra. Ao escrever as equações desta forma, estamos fazendo o uso extensivo de A fórmula de Euler para expressar sinusóides em termos de exponenciais complexas, que são muito mais fáceis de manipular. (Da mesma forma, pela escrita
ciclos por amostra. Ao escrever as equações desta forma, estamos fazendo o uso extensivo de A fórmula de Euler para expressar sinusóides em termos de exponenciais complexas, que são muito mais fáceis de manipular. (Da mesma forma, pela escrita 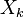 em forma polar , obtemos imediatamente a amplitude do senóide
em forma polar , obtemos imediatamente a amplitude do senóide 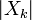 e a fase do argumento complexo.) Uma sutileza importante desta representação, aliasing, é discutida abaixo.
e a fase do argumento complexo.) Uma sutileza importante desta representação, aliasing, é discutida abaixo.
Note-se que o factor de normalização multiplicando o DFT e IDFT (aqui 1 e 1 / N) e os sinais dos expoentes são meramente convenções, e diferem em alguns tratamentos. Os únicos requisitos destas convenções são de que a DFT e IDFT tem expoentes de sinal oposto e que o produto de seus fatores de normalização de 1 / N. Uma normalização de 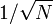 tanto para o DFT e IDFT faz com que as transformações unitária, que tem algumas vantagens teóricas, mas muitas vezes é mais prático em computação numérica para realizar o escalonamento de uma só vez como descrito acima (e uma unidade de escalonamento pode ser conveniente em outras formas).
tanto para o DFT e IDFT faz com que as transformações unitária, que tem algumas vantagens teóricas, mas muitas vezes é mais prático em computação numérica para realizar o escalonamento de uma só vez como descrito acima (e uma unidade de escalonamento pode ser conveniente em outras formas).
(A convenção de um sinal negativo no expoente é muitas vezes conveniente, porque isso significa que 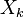 é a amplitude de um "frequência positiva"
é a amplitude de um "frequência positiva" 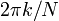 . Equivalentemente, o DFT é frequentemente considerada como um filtro de comparação: quando se olha para uma frequência de 1, um correlaciona o sinal de entrada com uma freqüência de -1).
. Equivalentemente, o DFT é frequentemente considerada como um filtro de comparação: quando se olha para uma frequência de 1, um correlaciona o sinal de entrada com uma freqüência de -1).
Na discussão a seguir os termos "seqüência" e "vector" serão considerados intercambiáveis.
Propriedades
Perfeição
A transformada de Fourier discreta é uma invertida, transformação linear
com 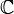 denotando o conjunto de números complexos . Em outras palavras, para qualquer n> 0, um complexo -dimensional vector N tem um DFT e uma IDFT que são, por sua vez vectores N dimensionais complexos.
denotando o conjunto de números complexos . Em outras palavras, para qualquer n> 0, um complexo -dimensional vector N tem um DFT e uma IDFT que são, por sua vez vectores N dimensionais complexos.
Ortogonalidade
Os vectores 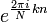 para homem base ortogonal sobre o conjunto de N-dimensional vetores complexos:
para homem base ortogonal sobre o conjunto de N-dimensional vetores complexos:
onde 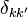 é o Kronecker delta. Esta condição de ortogonalidade pode ser utilizado para derivar a fórmula para a IDFT da definição da DFT, e é equivalente à propriedade unitariedade abaixo.
é o Kronecker delta. Esta condição de ortogonalidade pode ser utilizado para derivar a fórmula para a IDFT da definição da DFT, e é equivalente à propriedade unitariedade abaixo.
O teorema de Plancherel e teorema de Parseval
Se X e Y k k são os DFTs de xn e y, respectivamente, então n o Plancherel teorema:
onde a estrela denota conjugação complexa. Teorema de Parseval é um caso especial do teorema de Plancherel e estados:
Estes teoremas também são equivalentes à condição unitária abaixo.
Periodicidade
Se a expressão que define o DFT é avaliada para todos os inteiros 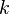 em vez de apenas para
em vez de apenas para 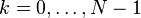 , Então a sequência infinita resultante é uma extensão periódica da DFT, periódica com período N.
, Então a sequência infinita resultante é uma extensão periódica da DFT, periódica com período N.
A periodicidade pode ser demonstrado directamente a partir da definição:
onde usamos o fato de que 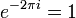 . Da mesma maneira pode-se mostrar que a fórmula IDFT leva a uma extensão periódica.
. Da mesma maneira pode-se mostrar que a fórmula IDFT leva a uma extensão periódica.
O teorema de deslocamento
Multiplicando 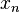 por uma fase linear
por uma fase linear 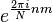 para algum inteiro
para algum inteiro 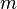 corresponde a um deslocamento circular da saída
corresponde a um deslocamento circular da saída 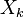 :
: 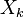 é substituído por
é substituído por 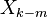 , Onde o subscrito é interpretado módulo
, Onde o subscrito é interpretado módulo 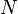 (Ou seja, periodicamente). Da mesma forma, um deslocamento circular da entrada
(Ou seja, periodicamente). Da mesma forma, um deslocamento circular da entrada 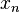 corresponde a multiplicar a saída
corresponde a multiplicar a saída 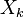 por uma fase linear. Matematicamente, se
por uma fase linear. Matematicamente, se 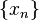 representa o vector x seguida
representa o vector x seguida
- se
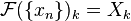
- em seguida
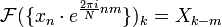
- e
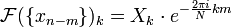
Teorema da convolução Circular e teorema de correlação cruzada
O teorema de convolução para o tempo contínuo e discreto transformadas de Fourier que indica uma convolução de duas sequências infinitas pode ser obtido como a transformada inversa do produto das transformadas individuais. Com sequências e transformações de comprimento N, A circularidade surge:
A quantidade entre parênteses é 0 para todos os valores de 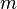 exceto os da forma
exceto os da forma 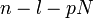 , Onde
, Onde 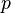 é um número inteiro qualquer. Nessas valores, é 1. Por conseguinte, pode ser substituído por uma soma infinita de Funções delta Kronecker, e continuamos em conformidade. Note que também pode estender os limites da
é um número inteiro qualquer. Nessas valores, é 1. Por conseguinte, pode ser substituído por uma soma infinita de Funções delta Kronecker, e continuamos em conformidade. Note que também pode estender os limites da 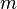 para o infinito, com o entendimento de que o
para o infinito, com o entendimento de que o 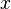 e
e 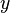 sequências são definidas como 0 fora [0, N-1]:
sequências são definidas como 0 fora [0, N-1]:
que é a convolução da 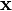 seqüência com um estendido periodicamente
seqüência com um estendido periodicamente 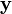 sequência definida por:
sequência definida por:
Do mesmo modo, pode ser mostrado que:
o qual é a correlação cruzada de 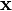 e
e 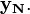
Uma avaliação directa da convolução ou correlação somatório, acima, requer 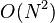 operações. Um método indirecto, usando transformações, podem tirar proveito da
operações. Um método indirecto, usando transformações, podem tirar proveito da 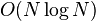 eficiência do Fast Fourier Transform (FFT) para alcançar um desempenho muito melhor. Além disso, convoluções podem ser usadas para calcular DFTs eficientemente através Algoritmo FFT e Rader Algoritmo FFT Bluestein.
eficiência do Fast Fourier Transform (FFT) para alcançar um desempenho muito melhor. Além disso, convoluções podem ser usadas para calcular DFTs eficientemente através Algoritmo FFT e Rader Algoritmo FFT Bluestein.
Os métodos também têm sido desenvolvidas para utilizar a convolução circular, como parte de um processo eficiente que atinge (não circular) convolução normal com um 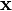 ou
ou 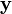 sequência potencialmente muito mais tempo do que o tamanho prático transformar (N). Dois desses métodos são chamados sobrepõem-save e sobrepor-adicionar.
sequência potencialmente muito mais tempo do que o tamanho prático transformar (N). Dois desses métodos são chamados sobrepõem-save e sobrepor-adicionar.
Trigonometria polinômio de interpolação
O trigonométricas polinômios interpolação
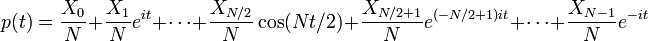 para
para 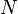 até mesmo,
até mesmo, 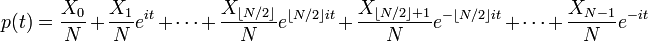 para
para 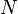 impar,
impar,
onde os coeficientes k X / N são fornecidos pelo DFT de N x acima, satisfaz a propriedade de interpolação 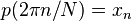 para
para 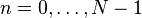 .
.
Para ainda 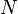 , Observe que o Componente Nyquist
, Observe que o Componente Nyquist 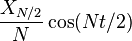 é tratada de forma especial.
é tratada de forma especial.
Esta interpolação não é único: aliasing implica que se pode adicionar N para qualquer das frequências complexo-sinusoidais (por exemplo, mudando 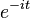 para
para 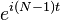 ) Sem alterar a propriedade de interpolação, mas dando valores diferentes entre o
) Sem alterar a propriedade de interpolação, mas dando valores diferentes entre o 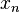 pontos. A escolha acima, no entanto, é típico, porque tem duas propriedades úteis. Em primeiro lugar, é constituída por sinusóides cujas frequências têm as menores amplitudes possíveis, e, portanto, minimiza a raiz quadrada da média declive
pontos. A escolha acima, no entanto, é típico, porque tem duas propriedades úteis. Em primeiro lugar, é constituída por sinusóides cujas frequências têm as menores amplitudes possíveis, e, portanto, minimiza a raiz quadrada da média declive 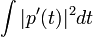 da função de interpolação. Em segundo lugar, se o
da função de interpolação. Em segundo lugar, se o 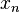 São números reais, em seguida,
São números reais, em seguida, 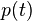 também é real.
também é real.
Em contraste, a mais óbvia interpolação polinomial trigonométrica é aquele em que as frequências variam de 0 a 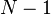 (Em vez de mais ou menos
(Em vez de mais ou menos  para
para  como acima), semelhante ao da fórmula DFT inversa. Esta interpolação não minimiza a inclinação, e geralmente não é de valor real para real
como acima), semelhante ao da fórmula DFT inversa. Esta interpolação não minimiza a inclinação, e geralmente não é de valor real para real 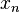 ; seu uso é um erro comum.
; seu uso é um erro comum.
A unitário DFT
Outra maneira de ver o DFT é notar que na discussão acima, a TFD pode ser expresso como um Matriz Vandermonde:
onde
é uma primitiva Nth raiz da unidade. A transformação inversa é então dado por: o inverso da matriz acima:
Com constantes de normalização unitárias 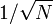 , Torna-se um DFT transformação unitária, definida por uma matriz unitária:
, Torna-se um DFT transformação unitária, definida por uma matriz unitária:
onde det () é o determinante função. O determinante é o produto dos valores próprios, que são sempre 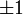 ou
ou 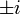 como descrito abaixo. Num espaço vectorial real, uma transformação unitária pode ser pensado como uma simples rotação rígida do sistema de coordenadas, e todas as propriedades de uma rotação rígida pode ser encontrado no DFT unitária.
como descrito abaixo. Num espaço vectorial real, uma transformação unitária pode ser pensado como uma simples rotação rígida do sistema de coordenadas, e todas as propriedades de uma rotação rígida pode ser encontrado no DFT unitária.
A ortogonalidade da DFT é agora expressa como um orthonormality condição (que surge em muitas áreas da matemática, tal como descrito em raiz da unidade):
Se 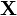 é definida como o DFT unitária do vector
é definida como o DFT unitária do vector 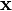 em seguida
em seguida
e o Plancherel teorema é expresso como:
Se vemos o DFT como apenas uma transformação que simplesmente especifica os componentes de um vetor em um novo sistema de coordenadas coordenar, em seguida, o acima é apenas a afirmação de que o produto escalar de dois vetores é preservado sob uma transformação DFT unitário. Para o caso especial 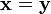 , Isto implica que o comprimento de um vector é preservado como bem esta é apenas Teorema de Parseval:
, Isto implica que o comprimento de um vector é preservado como bem esta é apenas Teorema de Parseval:
Expressando a DFT inversa em termos da DFT
Uma propriedade útil da DFT que é a DFT inversa pode ser facilmente expressa em termos de (para a frente) DFT, através de vários truques "" bem conhecidos. (Por exemplo, em computações, é muitas vezes conveniente para implementar apenas uma transformação Fourier rápida correspondente para transformar uma direcção e, em seguida, para se transformar o outro sentido a partir da primeira.)
Em primeiro lugar, podemos calcular a DFT inversa, invertendo as entradas:
(Como de costume, os subscritos são interpretados modulo 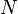 ; Assim, por
; Assim, por 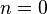 , Temos
, Temos 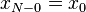 .)
.)
Em segundo lugar, também se pode conjugar as entradas e saídas:
Em terceiro lugar, uma variante deste truque de conjugação, que é por vezes preferível, porque não requer nenhuma modificação dos valores de dados, envolve a troca partes reais e imaginárias (que pode ser feito em um computador simplesmente modificando ponteiros). Definir swap ( 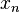 ) Como
) Como 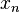 com as suas partes real e imaginária trocada, isto é, se
com as suas partes real e imaginária trocada, isto é, se 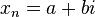 então trocar (
então trocar ( 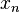 ) É
) É 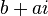 . Equivalentemente, swap (
. Equivalentemente, swap ( 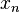 ) É igual
) É igual  . Em seguida
. Em seguida
Isto é, a transformação inversa é o mesmo que a transformação para a frente com as suas partes real e imaginária trocado para entrada e saída, até uma normalização (Duhamel et ai., 1988).
O truque de conjugação também pode ser utilizado para definir uma nova transformação, intimamente relacionado com a TFD, que é involutary, isto é, qual é o seu próprio inversa. Em particular, 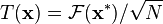 é claramente o seu próprio inversa:
é claramente o seu próprio inversa: 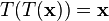 . Uma transformação involutary intimamente relacionados (por um factor de (1 + i) / √2) é
. Uma transformação involutary intimamente relacionados (por um factor de (1 + i) / √2) é 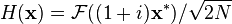 , Uma vez que o
, Uma vez que o 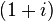 fatores na
fatores na 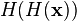 2. Para cancelar a entradas reais
2. Para cancelar a entradas reais 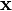 , A parte real
, A parte real 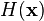 não é outro senão o Hartley discreta transformação, que também é involutary.
não é outro senão o Hartley discreta transformação, que também é involutary.
Valores e vectores próprios
Os valores próprios da matriz DFT são simples e bem conhecida, enquanto que os vectores próprios são complicadas, não exclusivo, e são objecto de investigação em curso.
Considere a forma unitária 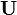 definido acima para o DFT de comprimento
definido acima para o DFT de comprimento 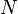 , Onde
, Onde 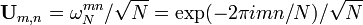 . Esta matriz satisfaz a equação:
. Esta matriz satisfaz a equação:
Isto pode ser visto a partir das propriedades acima inversos: operando 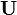 duas vezes dá os dados originais na ordem inversa, de modo a funcionar
duas vezes dá os dados originais na ordem inversa, de modo a funcionar 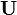 quatro vezes devolve os dados originais e é, portanto, a matriz identidade. Isto significa que os valores próprios
quatro vezes devolve os dados originais e é, portanto, a matriz identidade. Isto significa que os valores próprios 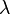 satisfazer um equação característica:
satisfazer um equação característica:
Portanto, os valores próprios de 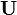 são a quarta raízes da unidade:
são a quarta raízes da unidade: 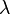 é 1, -1, + I, ou - i.
é 1, -1, + I, ou - i.
Uma vez que existem apenas quatro autovalores distintos para este 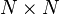 matriz, eles têm alguns multiplicidade . A multiplicidade dá o número de autovetores linearmente independentes correspondentes a cada valor próprio. (Note que existem N autovetores independentes; uma matriz unitária é nunca defeituoso.)
matriz, eles têm alguns multiplicidade . A multiplicidade dá o número de autovetores linearmente independentes correspondentes a cada valor próprio. (Note que existem N autovetores independentes; uma matriz unitária é nunca defeituoso.)
O problema da sua multiplicidade foi resolvido por McClellan e Parks (1972), embora mais tarde foi demonstrado que foram equivalentes a um problema resolvido por Gauss (Dickinson e Steiglitz, 1982). A multiplicidade depende do valor de 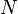 módulo 4, e é dada pela seguinte tabela:
módulo 4, e é dada pela seguinte tabela:
| N tamanho | λ = 1 | λ = -1 | λ = - i | λ = + i |
|---|---|---|---|---|
| 4 m | m + 1 | m | m | m - 1 |
| 4 m + 1 | m + 1 | m | m | m |
| 4 m + 2 | m + 1 | m + 1 | m | m |
| 4 m + 3 | m + 1 | m + 1 | m + 1 | m |
Infelizmente, nenhuma fórmula analítica simples para os autovetores é conhecido. Além disso, os vectores próprios não são únicos porque qualquer combinação linear de vectores próprios para o mesmo valor próprio é também um autovetor para esse valor próprio. Vários pesquisadores propuseram diferentes opções de autovetores, selecionado para satisfazer propriedades úteis, como ortogonalidade e ter formas "simples" (por exemplo, McClellan e Parques, 1972; Dickinson e Steiglitz, 1982; Grünbaum, 1982; Atakishiyev e Lobo, 1997;. Candan et al, 2000; Hanna et al., 2004).
A escolha de vectores próprios da matriz de DFT tornou-se importante em anos recentes, a fim de definir um análogo discreta do transformar-de Fourier fracionário matriz DFT podem ser tomadas para potências fracionárias por exponencializando os valores próprios (por exemplo, Rubio e Santhanam, 2005). Para o contínua com transformada de Fourier, as autofunções ortogonais naturais são a Funções de Hermite, assim vários análogos discretos destes têm sido empregados como os vectores próprios da DFT, tais como o Polinômios Kravchuk (Atakishiyev e Wolf, 1997). O "melhor" escolha de autovetores para definir uma transformada de Fourier discreta fracionada permanece uma questão em aberto, no entanto.
O DFT entrada real-
Se 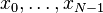 são números reais , já que muitas vezes estão em aplicações práticas, então o DFT obedece à simetria:
são números reais , já que muitas vezes estão em aplicações práticas, então o DFT obedece à simetria:
onde a estrela denota conjugação complexa e os subscritos são interpretados módulo N.
Portanto, a saída de DFT para entradas reais é metade redundante, e obtém-se a informação completa apenas olhando para cerca de metade das saídas 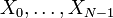 . Neste caso, o elemento de "DC"
. Neste caso, o elemento de "DC" 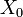 é puramente real, e até mesmo para N o elemento "Nyquist"
é puramente real, e até mesmo para N o elemento "Nyquist" 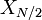 também é real, então há exatamente N não redundantes números reais no primeiro semestre + elemento Nyquist da saída do complexo X.
também é real, então há exatamente N não redundantes números reais no primeiro semestre + elemento Nyquist da saída do complexo X.
Uso A fórmula de Euler, o polinômio trigonométrico interpolação, em seguida, pode ser interpretado como uma soma de funções seno e cosseno.
Generalized / deslocou DFT
É possível deslocar a amostragem transformar no tempo e / ou no domínio da frequência por alguns turnos uma real e b, respectivamente. Isso às vezes é conhecido como um DFT generalizada (ou GDFT), também chamado de deslocados DFT ou compensar DFT, e tem propriedades análogas à DFT comum:
Na maioria das vezes, muda de 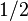 (Metade de uma amostra) são utilizados. Enquanto o DFT ordinária corresponde a um sinal periódico no tempo e domínios de frequência,
(Metade de uma amostra) são utilizados. Enquanto o DFT ordinária corresponde a um sinal periódico no tempo e domínios de frequência,  produz um sinal que é anti-periódica no domínio da frequência (
produz um sinal que é anti-periódica no domínio da frequência ( 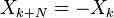 ) E vice-versa para
) E vice-versa para 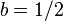 . Assim, no caso específico de
. Assim, no caso específico de 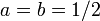 é conhecido como um momento ímpar-ímpar de frequência transformada de Fourier discreta (ou O 2 DFT). Tal deslocado transformações são mais frequentemente usado para dados simétricas, para representar diferentes simetrias de fronteira, e para os dados em tempo real, simétrica que correspondem a diferentes formas de o discreto cosseno e transformações seno.
é conhecido como um momento ímpar-ímpar de frequência transformada de Fourier discreta (ou O 2 DFT). Tal deslocado transformações são mais frequentemente usado para dados simétricas, para representar diferentes simetrias de fronteira, e para os dados em tempo real, simétrica que correspondem a diferentes formas de o discreto cosseno e transformações seno.
Outra opção interessante é 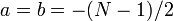 , Que é chamado o DFT centrada (ou CDFT). O DFT centrado tem a propriedade útil que, quando
, Que é chamado o DFT centrada (ou CDFT). O DFT centrado tem a propriedade útil que, quando 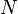 é um múltiplo de quatro, todos os quatro de seus valores próprios (ver acima) tem multiplicidades iguais (Rubio e Santhanam, 2005).
é um múltiplo de quatro, todos os quatro de seus valores próprios (ver acima) tem multiplicidades iguais (Rubio e Santhanam, 2005).
A transformada discreta de Fourier pode ser visto como um caso especial de o transformada z, avaliada sobre o círculo unitário no plano complexo; mais gerais transformadas z correspondem a mudanças complexas a e b acima.
Multidimensional DFT
A DFT ordinária calcula a transformação de um conjunto de dados "unidimensional": uma sequência (ou array) 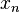 que é uma função de uma variável discreta
que é uma função de uma variável discreta 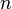 . Mais geralmente, pode-se definir a DFT multidimensional de uma matriz multidimensional
. Mais geralmente, pode-se definir a DFT multidimensional de uma matriz multidimensional 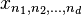 que é uma função de
que é uma função de 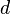 variáveis discretas
variáveis discretas 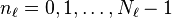 para
para 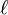 em
em 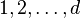 :
:
onde 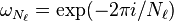 como acima e o
como acima e o 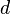 índices de saída executado a partir de
índices de saída executado a partir de 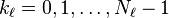 . Este é mais compacta expressa em notação vetor, onde definimos
. Este é mais compacta expressa em notação vetor, onde definimos 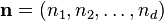 e
e 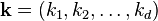 como
como 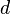 vectores dimensionais de índices de 0 a
vectores dimensionais de índices de 0 a 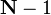 , Que definimos como
, Que definimos como 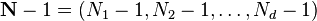 :
:
onde a divisão 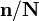 é definido como
é definido como 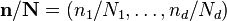 a ser realizada elemento a elemento, ea soma denota o conjunto de somas aninhadas acima.
a ser realizada elemento a elemento, ea soma denota o conjunto de somas aninhadas acima.
O inverso da DFT multi-dimensional é, análogo ao caso unidimensional, dada por:
O multidimensional DFT tem uma interpretação simples. Assim como o DFT unidimensional expressa a entrada 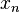 como uma superposição de sinusoidais, a DFT multidimensional expressa a entrada como uma superposição de ondas planas, ou sinusóides oscilando ao longo da direção
como uma superposição de sinusoidais, a DFT multidimensional expressa a entrada como uma superposição de ondas planas, ou sinusóides oscilando ao longo da direção  no espaço e com uma amplitude
no espaço e com uma amplitude 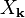 . Tal decomposição é de grande importância para tudo, desde processamento digital de imagem (d = 2) para resolver equações diferenciais parciais em três dimensões (d = 3), quebrando-se a solução em ondas planas.
. Tal decomposição é de grande importância para tudo, desde processamento digital de imagem (d = 2) para resolver equações diferenciais parciais em três dimensões (d = 3), quebrando-se a solução em ondas planas.
Computacionalmente, a DFT multidimensional é simplesmente a composição de uma sequência de DFTs unidimensional ao longo de cada dimensão. Por exemplo, no caso bidimensional 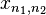 pode-se calcular o primeiro
pode-se calcular o primeiro 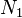 DFTs independentes das linhas (isto é, ao longo
DFTs independentes das linhas (isto é, ao longo 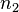 ) Para formar uma nova matriz
) Para formar uma nova matriz 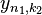 E, em seguida calcular a
E, em seguida calcular a 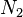 DFTs independentes de
DFTs independentes de 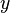 ao longo das colunas (juntamente
ao longo das colunas (juntamente 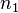 ) Para formar o resultado final
) Para formar o resultado final 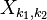 . Ou, pode-se transformar as colunas e, em seguida, as linhas-a ordem é irrelevante porque as somas aninhadas acima trajeto .
. Ou, pode-se transformar as colunas e, em seguida, as linhas-a ordem é irrelevante porque as somas aninhadas acima trajeto .
Devido a isto, dado um modo para calcular um DFT unidimensional (por exemplo, um algoritmo FFT unidimensional comum), um imediatamente tem uma forma de calcular eficientemente o DFT multidimensional. Isto é conhecido como um algoritmo de linha-coluna, embora também existam intrinsecamente algoritmos de FFT multidimensional.
O entradas reais multidimensional DFT
Se as entradas 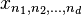 são números reais , como são frequentemente em aplicações de ordem prática, as saídas DFT tem uma simetria conjugado semelhante ao caso unidimensional acima:
são números reais , como são frequentemente em aplicações de ordem prática, as saídas DFT tem uma simetria conjugado semelhante ao caso unidimensional acima:
onde a estrela indica a conjugação complexa ea 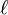 subscrito -ésimo é interpretado módulo
subscrito -ésimo é interpretado módulo 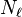 (Por
(Por 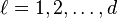 ).
).
Aplicações
A DFT viu ampla utilização através de um grande número de campos; temos apenas esboçar alguns exemplos abaixo (ver também as referências ao final). Todos os aplicativos do DFT dependem crucialmente da disponibilidade de um algoritmo rápido para computar transformadas de Fourier discreta e seus inversos, um Transformada de Fourier rápido.
A análise espectral
Quando o DFT é usado para análise espectral, a 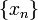 seqüência geralmente representa um conjunto finito de amostras de tempo-uniformemente espaçados de algum sinal
seqüência geralmente representa um conjunto finito de amostras de tempo-uniformemente espaçados de algum sinal 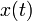 , Em que t representa o tempo. A conversão de tempo contínuo de amostras (de tempo discreto) altera a subjacentes Transformada de Fourier de x (t) para uma Fourier de tempo discreto transformar (DTFT), que geralmente implica um tipo de distorção chamada aliasing. Escolha de uma taxa de amostra adequado (ver Frequência de Nyquist) é a chave para minimizar essa distorção. Do mesmo modo, a conversão de uma sequência muito longa (ou infinito) para um tamanho manuseável implica um tipo de distorção chamada fugas, que se manifesta como uma perda de detalhe (resolução aka) no TFTD. Escolha de um comprimento sub-sequência apropriada é a chave primária para minimizar esse efeito. Quando os dados disponíveis (e tempo para processá-lo) é mais do que o montante necessário para atingir a resolução de freqüência desejada, uma técnica padrão é para executar várias DFTs, por exemplo, para criar uma espectrograma. Se o resultado desejado é um espectro de potência e ruído aleatório ou está presente nos dados, calcular a média dos componentes de grandeza da DFTs múltiplos é um procedimento útil para reduzir a variância do espectro (também chamado de periodogramas neste contexto); Dois exemplos de tais técnicas são a E o método de Welch Método de Bartlett.
, Em que t representa o tempo. A conversão de tempo contínuo de amostras (de tempo discreto) altera a subjacentes Transformada de Fourier de x (t) para uma Fourier de tempo discreto transformar (DTFT), que geralmente implica um tipo de distorção chamada aliasing. Escolha de uma taxa de amostra adequado (ver Frequência de Nyquist) é a chave para minimizar essa distorção. Do mesmo modo, a conversão de uma sequência muito longa (ou infinito) para um tamanho manuseável implica um tipo de distorção chamada fugas, que se manifesta como uma perda de detalhe (resolução aka) no TFTD. Escolha de um comprimento sub-sequência apropriada é a chave primária para minimizar esse efeito. Quando os dados disponíveis (e tempo para processá-lo) é mais do que o montante necessário para atingir a resolução de freqüência desejada, uma técnica padrão é para executar várias DFTs, por exemplo, para criar uma espectrograma. Se o resultado desejado é um espectro de potência e ruído aleatório ou está presente nos dados, calcular a média dos componentes de grandeza da DFTs múltiplos é um procedimento útil para reduzir a variância do espectro (também chamado de periodogramas neste contexto); Dois exemplos de tais técnicas são a E o método de Welch Método de Bartlett.
A última fonte de distorção (ou talvez ilusão) é o próprio DFT, porque é apenas uma amostra discreta da TFTD, que é uma função de um domínio de frequência contínua. Isso pode ser mitigada ao aumentar a resolução da DFT. Este procedimento é ilustrado no de tempo discreto com transformada de Fourier artigo.
- O procedimento é por vezes referido como zero-estofamento, que é uma implementação específica usada em conjunto com o Fast Fourier Transform (FFT). A ineficiência de realizar multiplicações e adições com zero valorizado "amostras" é mais do que compensado pela eficiência inerente da FFT.
- Como já se referiu, o vazamento impõe um limite inerente a resolução do TFTD. Portanto, há um limite prático para o benefício que pode ser obtido a partir de um refinado DFT.
Compressão de dados
O campo de processamento de sinal digital depende fortemente de operações no domínio da frequência (ou seja, na Transformada de Fourier). Por exemplo, várias de imagem com perdas e os métodos de compressão de som empregar a transformada de Fourier discreta: o sinal é cortado em segmentos curtos, cada um é transformado, em seguida, os coeficientes de Fourier de altas frequências, que são assumidos para ser imperceptível, são descartados. O descompressor calcula a transformada inversa com base neste número reduzido de coeficientes de Fourier. (Aplicações de compressão utilizam frequentemente uma forma especializada da DFT, o transformação de coseno discreta ou, por vezes, o co-seno discreta modificada transformar.)
Equações diferenciais parciais
Transformadas de Fourier discretas são freqüentemente usados para resolver equações diferenciais parciais , onde novamente o DFT é usado como uma aproximação para a Séries de Fourier (que é recuperado no limite de infinito N). A vantagem dessa abordagem é que ela amplia o sinal em exponenciais complexas e inx, que são funções próprias de diferenciação: d / dx e inx = in e inx. Assim, na representação de Fourier, a diferenciação é simples: nós simplesmente multiplicar por dentro. A equação diferencial linear com coeficientes constantes é transformado em uma equação algébrica facilmente solucionáveis. Um em seguida, usa o DFT inversa para transformar o resultado de volta para a representação espacial comum. Este tipo de abordagem chama-se método espectral.
Multiplicação polinomial
Suponhamos que deseja calcular o produto polinomial c (x) = a (x) · b (x). O produto de expressão comum para os coeficientes de c envolve uma convolução linear (acíclico), onde os índices não "embrulhar ao redor." Isto pode ser escrito como uma convolução cíclico tomando os vectores de coeficiente para um (x) e b (x) com o termo constante em primeiro lugar, em seguida, adicionando os zeros de modo a que o coeficiente de vectores resultante e b têm uma dimensão d> ° (a (x) ) + ° (b (x)). Em seguida,
Em que C é o vector dos coeficientes de C (x), e o operador de convolução 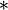 é definido assim
é definido assim
Mas convolução torna-se sob a multiplicação DFT:
Aqui, o produto é tomado vector de elemento a elemento. Assim, os coeficientes do polinómio produto c (X) são apenas os termos 0, ..., ° (a (x)) + ° (b (x)) do vector de coeficiente
Com um Transformada Rápida de Fourier, o algoritmo resultante leva O (N log N) operações aritméticas. Devido à sua simplicidade e rapidez, o Cooley-Tukey algoritmo FFT, que é limitado a tamanhos compósitos, é muitas vezes escolhida para a operação de transformação. Neste caso, d deve ser escolhido como o menor número inteiro maior do que a soma dos graus de entrada polinomiais que é factorizar em pequenos factores primos (por exemplo, 2, 3, e 5, dependendo da implementação de FFT).
Multiplicação de inteiros grandes
O mais rápido conhecido os algoritmos para a multiplicação de grandes números inteiros usar o método de multiplicação polinomial descrito acima. Os inteiros podem ser tratados como o valor de um polinómio avaliado especificamente na base número, com os coeficientes do polinómio correspondente aos dígitos em que a base. Depois de multiplicação polinomial, uma relativamente baixa complexidade passo carry-propagação completa a multiplicação.
Transformação de Fourier discreta Alguns pares
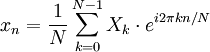 | 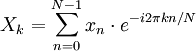 | Nota |
|---|---|---|
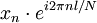 | 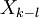 | Mudança teorema |
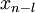 | 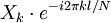 | |
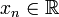 | 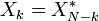 | DFT real |
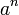 | 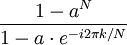 | |
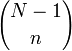 | 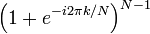 |
Derivação como séries de Fourier
O DFT pode ser derivada como um truncamento da Séries de Fourier de uma sequência periódica de impulsos.
TFD sobre os outros do que os números complexos campos
Muitas das propriedades do DFT depende apenas do facto 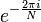 é um raiz primitiva da unidade, às vezes denotado
é um raiz primitiva da unidade, às vezes denotado 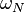 ou
ou 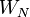 (De modo que
(De modo que 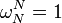 ). Essas propriedades incluem a integralidade, ortogonalidade, Plancherel / Parseval, periodicidade, deslocamento, convolução, e propriedades unitariedade acima, bem como muitos algoritmos FFT. Por esta razão, a transformada de Fourier discreta pode ser definida usando raízes da unidade em outros do que os números complexos campos; Para obter mais informações, consulte Transformada de Fourier discreta (geral).
). Essas propriedades incluem a integralidade, ortogonalidade, Plancherel / Parseval, periodicidade, deslocamento, convolução, e propriedades unitariedade acima, bem como muitos algoritmos FFT. Por esta razão, a transformada de Fourier discreta pode ser definida usando raízes da unidade em outros do que os números complexos campos; Para obter mais informações, consulte Transformada de Fourier discreta (geral).