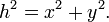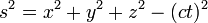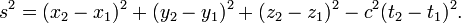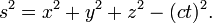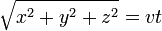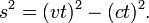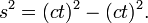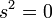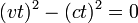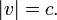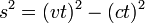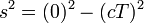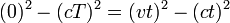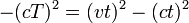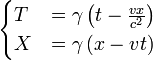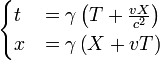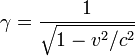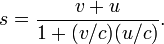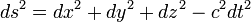Introdução à relatividade especial

Albert Einstein, durante uma palestra em Viena em 1921

Em física , a relatividade especial é um direito fundamental teoria relativa espaço e tempo , desenvolvida por Albert Einstein em 1905 como uma modificação do Relatividade de Galileu. (Veja " História da relatividade especial "para uma conta detalhada e as contribuições de Hendrik Lorentz e Henri Poincaré.) A teoria foi capaz de explicar alguns prensagem teóricas e experimentais em questões da física do tempo envolvendo luz e electrodinâmica, tais como a falha de 1887 Experiência de Michelson-Morley, que teve como objetivo medir diferenças na velocidade relativa de luz, devido à O movimento da Terra através do hipotético, e agora desacreditada, éter luminífero . O éter foi então considerado como o meio de propagação de ondas electromagnéticas , tais como a luz.

Einstein postulou que a velocidade da luz no espaço livre é o mesmo para todos observadores, independentemente de seu movimento em relação à fonte de luz, onde podemos pensar de um observador como uma entidade imaginária com um sofisticado conjunto de dispositivos de medição, em repouso com relação a si mesmo, que perfeitamente gravar as posições e os tempos de todos os eventos no espaço e tempo. Este postulado partia do pressuposto de que as equações de Maxwell do eletromagnetismo , que prever uma velocidade específica de luz no vácuo, segure em qualquer sistema de referência inercial e não, como se acreditava anteriormente, apenas no quadro do éter. Essa previsão contradizia as leis da mecânica clássica , que tinham sido aceites por séculos, com o argumento de que o tempo eo espaço não são fixos e em mudança fato de manter uma velocidade constante da luz, independentemente dos movimentos relativos de fontes e observadores. Abordagem de Einstein baseou-se experiências de pensamento, cálculos, eo princípio da relatividade, que é a noção de que todas as leis físicas deve aparecer o mesmo (isto é, assumir a mesma forma básica) para todos os observadores inerciais. Hoje, os cientistas são tão confortáveis com a idéia de que a velocidade da luz é sempre o mesmo que o medidor é agora definido como "o comprimento do trajecto percorrido pela luz no vácuo durante um intervalo de tempo de 1/299 792 458 de um segundo." Isto significa que a velocidade da luz é, por convenção 299 792 458 m / s (cerca de 1079 milhões quilômetros por hora, ou 671.000 mil milhas por hora).

As previsões da relatividade especial são quase idênticos aos da relatividade de Galileu para a maioria dos fenômenos cotidianos, nas quais velocidades são muito mais baixos do que a velocidade da luz, mas faz previsões diferentes, não-óbvios para objectos em movimento em velocidades muito altas. Estas previsões foram testadas experimentalmente em várias ocasiões desde o início da teoria e foram confirmadas por essas experiências. As principais previsões da relatividade especial são:

• Relatividade de simultaneidade: observadores que estão em movimento em relação ao outro podem desacordo sobre se dois eventos ocorreram ao mesmo tempo ou uma ocorreu antes do outro.
• Tempo dilatação (Um observador assistindo dois relógios idênticos, um movimento e um em repouso, vai medir o relógio movendo-se para assinalar mais lentamente)
• Contracção Comprimento (ao longo da direcção de movimento, uma haste móvel em relação a um observador será medido para ser mais curto do que uma haste idêntica em repouso), e
• O equivalência de massa e energia (escrita como E = mc ^2).

A relatividade especial prevê uma não linear Além fórmula velocidade que impede velocidades maiores do que a da luz de ser observada. Em 1908, Hermann Minkowski reformulou a teoria com base em diferentes postulados de natureza mais geométrica. Esta abordagem considera espaço e tempo como sendo diferentes componentes de uma única entidade, o espaço-tempo, que é "dividido" em maneiras diferentes por observadores em movimento relativo. Da mesma forma, a energia e quantidade de movimento são os componentes do quatro momentum, ea elétrica e campo magnético são os componentes do tensor eletromagnética.

Como relatividade de Galileu é considerado agora uma aproximação da relatividade especial válido para baixas velocidades, a relatividade especial é considerada uma aproximação da teoria da relatividade geral válido para fraco campos gravitacionais. A relatividade geral postula que as leis físicas devem aparecer a mesma para todos os observadores (uma aceleração quadro de referência sendo equivalente a um em que um gravitacionais atos de campo), e que a gravitação é o efeito da curvatura do espaço-tempo causada por energia (incluindo massa).

A física clássica e eletromagnetismo

Através da era entre Newton e em torno do início do século 20, o desenvolvimento da física clássica tinha feito grandes progressos. Aplicação de Newton lei do inverso do quadrado para a gravidade era a chave para desbloquear uma grande variedade de eventos físicos, de calor para luz , e cálculo feito o cálculo direto destes efeitos tratável. Com o tempo, novas técnicas matemáticas, nomeadamente a Lagrangian, muito simplificada a aplicação destas leis físicas para os problemas mais complexos.

Como a eletricidade eo magnetismo foram mais bem explorado, tornou-se claro que os dois conceitos foram relacionados. Ao longo do tempo, este trabalho culminou com as equações de Maxwell , um conjunto de quatro equações que podem ser utilizados para calcular a totalidade do electromagnetismo. Um dos resultados mais interessantes da aplicação destas equações é que era possível construir uma onda de auto-sustentação de campos eléctricos e magnéticos, que poderia propagam através do espaço. Quando reduzida, a matemática demonstraram que a velocidade de propagação foi dependente de duas constantes universais, e a sua razão foi a velocidade da luz . Luz era uma onda eletromagnética.

Segundo o modelo clássico, ondas são deslocamentos dentro de um médio. No caso da luz, as ondas foram pensados para ser deslocamentos de um meio especial conhecido como o éter luminífero , que se estendeu por todo o espaço. Sendo este o caso, a luz viaja em seu próprio quadro de referência, a estrutura do éter. De acordo com o Galileu transformar, devemos ser capazes de medir a diferença de velocidades entre a armação do éter e qualquer outro - um quadro universal no passado.

Projetar uma experiência para realmente realizar essa medição se revelado muito difícil, no entanto, como as velocidades e tempo envolvidos feita uma medição precisa difícil. O problema da medida acabou por ser resolvido com a Experiência de Michelson-Morley. Para surpresa de todos, nenhum movimento relativo foi visto. Ou o éter estava viajando na mesma velocidade que a Terra, difícil de imaginar dado movimento complexo da Terra, ou não havia éter. Experimentos de acompanhamento testou várias possibilidades, e pelo início do século 20 foi se tornando cada vez mais difícil escapar à conclusão de que não existia o éter.

Estas experiências mostraram que todos os luz simplesmente não seguiu a transformação de Galileu. E, no entanto, ficou claro que os objetos físicos a luz emitida, o que levou a problemas não resolvidos. Se fosse para realizar a experiência no trem por "lançar luz" em vez de bolas, se a luz não segue a transformação de Galileu, em seguida, os observadores não devem concordar com os resultados. No entanto, era evidente que o universo discordou; sistemas físicos conhecidos por serem em grandes velocidades, como estrelas distantes, tiveram física que eram tão semelhante ao nosso, como medições permitido. Algum tipo de transformação teve de ser agindo em luz, ou melhor, uma única transformação para ambos luz e matéria.

O desenvolvimento de uma transformação adequada para substituir a transformação de Galileu é a base da relatividade especial.

Invariância de comprimento: a imagem euclidiana

Teorema de Pitágoras

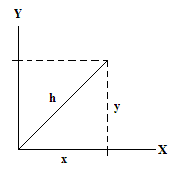
Na relatividade especial, o espaço eo tempo são unidos em um continuum quadridimensional chamado unificada espaço-tempo. Para ganhar uma sensação de que o espaço-tempo é como, devemos primeiro olhar para o espaço euclidiano da física newtoniana clássica. Esta abordagem para explicar a teoria da relatividade especial começa com o conceito de " comprimento ".

Na experiência cotidiana, parece que o comprimento de objetos continua a ser o mesmo, não importa como eles são rodados ou movidos de um lugar para outro; como resultado, o comprimento de um objecto simples não parece alterar ou é invariante. No entanto, como é mostrado nas figuras que se seguem, o que está realmente a ser sugerido é que o comprimento parece ser invariante em um sistema de coordenadas tridimensional.

O comprimento de uma linha num bidimensional sistema de coordenadas cartesianas, é dada pelo teorema de Pitágoras :

Um dos teoremas básicos de álgebra vectorial é que o comprimento de um vector não muda quando ele é rodado. No entanto, uma inspeção mais minuciosa nos diz que isto só é verdade se considerarmos rotações confinados ao plano. Se introduzirmos rotação na terceira dimensão, então podemos inclinar a linha para fora do avião. Neste caso, a projecção da linha no plano terá mais curto. Será que isso significa mudanças de comprimento da linha? - Obviamente, não. O mundo é tridimensional e num sistema Cartesiano de coordenadas 3D o comprimento é determinado pela versão tridimensional do teorema de Pitágoras:

Este é invariante sob todas as rotações. A aparente violação da invariância de comprimento só aconteceu porque estávamos "em falta" uma dimensão. Parece que, desde todas as direções em que um objeto pode ser inclinado ou arranjados são representados dentro de um sistema de coordenadas, o comprimento de um objeto não muda sob rotações. Com o tempo e espaço considerado fora do âmbito da própria física, sob a mecânica clássica de um sistema 3-dimensional de coordenadas é suficiente para descrever o mundo.

Note-se que a invariância de comprimento não é normalmente considerado um princípio ou lei, nem mesmo um teorema. É simplesmente uma declaração sobre a natureza fundamental do próprio espaço. O espaço como nós normalmente concebê-lo é chamado de tridimensional espaço euclidiano , pois sua estrutura geométrica é descrito pelos princípios da geometria euclidiana . A fórmula para a distância entre dois pontos é uma propriedade fundamental de um espaço euclidiano, ele é chamado o tensor métrico euclidiana (ou simplesmente a métrica euclidiana). Em geral, fórmulas de distância são chamados tensores métricos.

Note-se que as rotações são fundamentalmente relacionado com o conceito de comprimento. Na verdade, pode-se definir o comprimento ou a distância a ser aquilo que permanece o mesmo (é invariável) sob rotações, ou definir rotações para ser aquilo que manter o comprimento invariável. Dado qualquer um, é possível encontrar o outro. Se sabemos que a fórmula de distância, podemos descobrir a fórmula para transformar coordenadas em uma rotação. Se, por outro lado, temos a fórmula para rotações, então nós podemos descobrir a fórmula de distância.

A formulação de Minkowski: introdução de espaço-tempo

Depois de Einstein derivado relatividade especial formalmente a partir da (à primeira vista contra-intuitivo) suposição de que a velocidade da luz é a mesma para todos os observadores, Hermann Minkowski construído em abordagens matemáticas utilizadas na geometria não-euclidiana e sobre o trabalho matemático de Lorentz e Poincaré. Minkowski mostraram em 1908 que a nova teoria de Einstein também pode ser explicada através da substituição do conceito de um espaço de tempo e separada com um continuum quadridimensional chamado espaço-tempo. Este era um conceito inovador, e Roger Penrose disse que a relatividade não era verdadeiramente completo até que Minkowski reformulou o trabalho de Einstein.

O conceito de um espaço de quatro dimensões é difícil de visualizar. Ela pode ajudar no início de pensar simplesmente em termos de coordenadas. No espaço tridimensional, é necessário três números reais para se referir a um ponto. No Espaço de Minkowski, é preciso quatro números reais (três coordenadas espaciais e uma temporal de coordenadas) para se referir a um ponto em um instante de tempo. Neste ponto, indicada pelas quatro coordenadas, é chamado um evento. A distância entre dois eventos diferentes é chamado de intervalo de tempo-espaço.

Um caminho através do espaço-tempo de quatro dimensões (geralmente conhecida como espaço de Minkowski) é chamado de linha do mundo. Desde que especifica tanto a posição e tempo, uma partícula com uma linha de mundo conhecido tem uma trajetória completamente determinada e velocidade. Este é apenas como um gráfico do deslocamento de uma partícula que se move em linha reta contra o tempo decorrido. A curva contém a informação motional completa da partícula.

Da mesma maneira como a medição de distância no espaço 3D necessários todos os três coordenadas, que deve incluir o tempo, bem como os três coordenadas espaciais ao calcular a distância no espaço de Minkowski (daqui em diante chamado H). Num certo sentido, o intervalo de espaço-tempo fornece uma estimativa combinada da distância em dois eventos ocorrem no espaço, bem como o tempo que decorre entre a sua ocorrência.

Mas há um problema; tempo está relacionada com as coordenadas espaciais, mas elas não são equivalentes. Teorema de Pitágoras trata todas as coordenadas em pé de igualdade (ver espaço euclidiano para mais detalhes). Podemos trocar duas coordenadas espaciais sem alterar o comprimento, mas não podemos simplesmente trocar coordenar um espaço com o tempo - eles são fundamentalmente diferentes. É uma coisa totalmente diferente para dois eventos a serem separadas no espaço e para ser separados no tempo. Minkowski propôs que a fórmula para a distância necessária uma mudança. Ele descobriu que a fórmula correta era realmente muito simples, diferindo apenas por um sinal do teorema de Pitágoras:

onde C é uma constante e t é o tempo de coordenadas. A multiplicação por C, que tem a dimensões G T ^-1, converte o tempo para unidades de comprimento e esta constante tem o mesmo valor que a velocidade da luz . Assim, o intervalo de espaço-tempo entre dois acontecimentos distintos é dada pela

Há dois pontos importantes a serem observados. Em primeiro lugar, o tempo está a ser medida nas mesmas unidades como o comprimento multiplicando-o por um factor de conversão constante. Em segundo lugar, e mais importante, o tempo de coordenada tem um sinal diferente do que as coordenadas espaciais. Isto significa que, no espaço-tempo de quatro dimensões, uma coordenada é diferente dos outros e influencia a distância diferente. Este novo "distância" pode ser zero ou mesmo negativo. Esta nova fórmula de distância, o chamado métrica do espaço-tempo, está no coração da relatividade. Esta fórmula de distância é denominada tensor métrica de M. Este sinal negativo significa que um monte de nossa intuição sobre distâncias não podem ser levados diretamente por cima em intervalos de espaço-tempo. Por exemplo, o intervalo de espaço-tempo entre dois eventos separados no tempo e no espaço pode ser igual a zero (ver abaixo). A partir de agora, a fórmula termos distância e tensor métrico serão usados como sinônimos, como serão os termos de intervalo métrica e espaço-tempo de Minkowski.

Em Minkowski espaço-tempo a intervalo de tempo-espaço é o comprimento invariante, o comprimento 3D normal não seja necessário para ser invariante. O intervalo de espaço-tempo deve permanecer o mesmo sob rotações, mas comprimentos comuns podem mudar. Assim como antes, nos faltava uma dimensão. Note-se que tudo o que até agora é meramente definições. Definimos uma construção matemática de quatro dimensões, que tem uma fórmula especial para a distância, em que a distância que significa que se mantém as mesmas rotações sob (alternativamente, pode-se definir uma rotação para o que mantém o afastamento inalterado).

Agora vem a parte física. Rotações no espaço Minkowski tem uma interpretação diferente do que rotações comuns. Estas rotações correspondem às transformações de quadros de referência. Passando de um quadro de referência para outra corresponde ao rodar o espaço Minkowski. Uma justificação intuitiva para isso é dado abaixo, mas matematicamente este é um postulado dinâmico como supondo que as leis físicas devem permanecer o mesmo sob transformações galileanas (o que parece tão intuitivo que nós não costumamos reconhecê-lo para ser um postulado).

Desde rotações por definição deve manter a distância mesmo, passando para um quadro de referência diferente deve manter o intervalo de espaço-tempo entre dois eventos inalteradas. Esta exigência pode ser usado para derivar uma forma matemática explícita para a transformação que deve ser aplicado às leis da física (compare com a aplicação de transformações galileanas a leis clássicas) quando mudar quadros de referência. Estas transformações são chamados a Transformações de Lorentz. Assim como o Transformações de Galileu são o enunciado matemático do princípio da relatividade de Galileu na mecânica clássica, as transformações de Lorentz são a forma matemática do princípio da relatividade de Einstein. Leis da física deve permanecer o mesmo sob transformações de Lorentz. equações de Maxwell e A equação de Dirac satisfazer essa propriedade, e, portanto, eles são relativisticamente leis corretas (mas classicamente incorreta, uma vez que não transformar corretamente sob transformações galileanas).

Com a declaração da métrica Minkowski, o nome comum para a fórmula de distância dado acima, o fundamento teórico da relatividade especial está completa. Toda a base para a relatividade especial pode ser resumida pela declaração geométrica "mudanças de quadro de referência correspondem a rotações no espaço-tempo 4D Minkowski, que é definido para ter a fórmula de distância dada acima". As previsões dinâmicas únicas de haste SR partir desta propriedade geométrica do espaço-tempo. A relatividade especial pode ser dito para ser a física do espaço-tempo de Minkowski. Neste caso de espaço-tempo, existem seis rotações a serem considerados independentes. Três deles são as rotações padrão sobre um plano em duas direcções do espaço. Os outros três são rotações num plano de espaço e no tempo: Estas rotações corresponde a uma mudança de velocidade , e o Minkowski diagramas elaborados por ele descrever tais rotações.

Como já foi mencionado anteriormente, pode-se substituir fórmulas de distância com fórmulas de rotação. Em vez de começar com a invariância da métrica Minkowski como a propriedade fundamental do espaço-tempo, pode-se afirmar (como foi feito na física clássica com relatividade de Galileu), a forma matemática das transformações de Lorentz e exigem que as leis físicas ser invariante sob essas transformações. Isto não faz qualquer referência à geometria do espaço-tempo, mas irá produzir o mesmo resultado. Esta foi, de facto, a abordagem tradicional de SR, usado originalmente pelo próprio Einstein. No entanto, esta abordagem é muitas vezes considerado a oferecer uma visão menos e ser mais pesado do que o formalismo mais natural Minkowski.

Postulado de Einstein: a constância da velocidade da luz

Postulado de Einstein que a velocidade da luz é constante surge como uma consequência natural da formulação Minkowski.

Proposição 1:

Quando um objecto se desloca em C em um certo quadro de referência, o intervalo de espaço-tempo é zero.

Prova:

O intervalo de tempo-espaço entre a origem de eventos (0,0,0,0), e um evento (x, y, z, t) é

A distância percorrida por um objeto em movimento em velocidade v para t segundos é:

dando

Uma vez que a velocidade é igual a v c temos

Por isso, o intervalo de espaço-tempo entre os eventos de partida e de chegada é dada por

Proposição 2:

Um objeto que viaja na c em um quadro de referência está viajando em c em todos os referenciais.

Prova:

Deixe o objeto se mover com velocidade v quando observado a partir de um quadro de referência diferente. Uma mudança na estrutura de referência corresponde a uma rotação em M. Uma vez que o intervalo de espaço-tempo deve ser conservado sob rotação, o intervalo de espaço-tempo deve ser o mesmo em todos os quadros de referência. Em uma proposição que mostrou ser um zero no quadro de referência, pelo que deve ser igual a zero em todos os outros quadros de referência. Nós obtemos esse

o que implica

Os caminhos dos raios de luz têm um intervalo de zero espaço-tempo, e, portanto, todos os observadores irão obter o mesmo valor para a velocidade da luz. Por conseguinte, quando se assume que o universo tem quatro dimensões que estão relacionados pela fórmula de Minkowski, a velocidade da luz aparece como uma constante, e não necessita de ser assumida (postulado) ser constante como na abordagem original de Einstein a relatividade especial.

Relógio atrasos e haste: contrações mais sobre transformações de Lorentz

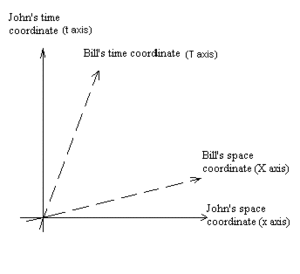
Outra consequência da invariância do intervalo de espaço-tempo é que os relógios aparece para ir mais lento em objetos que estão se movendo em relação ao observador. Isto é muito semelhante à forma como a projecção 2D de uma linha de rodado para a terceira dimensão parece ficam mais curtos. O comprimento não é conservada, simplesmente porque estamos ignorando uma das dimensões. Voltemos ao exemplo de John e Bill.

John observa o comprimento do intervalo de espaço-tempo de Bill como:

Considerando que Bill não acho que ele tenha viajado no espaço, assim escreve:

O intervalo de espaço-tempo, s ^2, é invariante. Ele tem o mesmo valor para todos os observadores, não importa quem as medidas que ou como eles estão se movendo em uma linha reta. Isto significa que o espaço-tempo intervalo de Bill é igual a observação de João de intervalo de espaço-tempo de Bill assim:

e

daqui

.

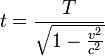Então, se João vê um relógio que está em repouso no registro quadro um segundo de Bill, John vai descobrir que suas próprias medidas de clock entre esses mesmos carrapatos um intervalo t, chamado coordenar o tempo, que é maior do que um segundo. Diz-se que os relógios em movimento lento, em relação aos observadores em repouso. Isto é conhecido como "relativista dilatação do tempo de um relógio em movimento ". O tempo que é medido no quadro resto do relógio (no quadro do Bill) é chamado de tempo adequado do relógio.

Na relatividade especial, portanto, mudanças na estrutura de referência afetar o tempo também. O tempo já não é absoluta. Não há relógio universalmente correta; o tempo corre em taxas diferentes para diferentes observadores.

Da mesma forma pode-se mostrar que John também vai observar medindo varas em repouso no planeta de Bill para ser mais curto na direção de movimento do que suas próprias varas de medição. Esta é uma predição conhecido como "relativista contração do comprimento de uma haste em movimento ". Se o comprimento de uma haste em repouso no planeta de Bill é X, então nós chamamos essa quantidade a comprimento adequado da haste. O x comprimento dessa mesma vara, medida no planeta de João, é chamado de comprimento de coordenadas, e dada por

.

Como coordenadas de Bill parecem John no instante em que eles passam um pelo outro

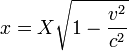Estas duas equações podem ser combinados para se obter a forma geral da transformação de Lorentz em uma dimensão espacial:

ou de modo equivalente:

onde o Fator de Lorentz é dada por

As fórmulas acima dos atrasos de clock e contrações de comprimento são casos especiais de transformação geral.

Alternativamente, essas equações para a dilatação do tempo ea contração do comprimento (aqui obtidos a partir da invariância do intervalo de espaço-tempo), podem ser obtidos diretamente a partir da transformação de Lorentz, definindo X = 0 para a dilatação do tempo, o que significa que o relógio está em repouso no frame de Bill, ou definindo T = 0 para comprimento de contracção, o que significa que deve John medir as distâncias para os pontos de extremidade da haste móvel, ao mesmo tempo.

Uma conseqüência das transformações de Lorentz é modificado fórmula da velocidade de adição:

Simultaneidade e relógio dessincronização

A última consequência do espaço-tempo de Minkowski é que os relógios aparece a ficar fora de fase uns com os outros ao longo do comprimento de um objecto em movimento. Isto significa que se um observador estabelece uma linha de relógios que são todos sincronizados para que todos eles ler ao mesmo tempo, em seguida, outro observador que está se movendo ao longo da linha em alta velocidade vai ver os relógios todos os tempos de leitura diferentes. Isto significa que os observadores que estão se movendo em relação ao outro ver os eventos diferentes como simultânea. Este efeito é conhecido como "Fase Relativistic" ou a "relatividade da simultaneidade". Relativistic fase é muitas vezes esquecido pelos alunos da relatividade especial, mas se for entendido, então fenômenos como o paradoxo dos gêmeos são mais fáceis de entender.

O "plano de simultaneidade" ou "superfície de simultaneidade" contém todos os acontecimentos que ocorrem no mesmo instante para um determinado observador. Os eventos que são simultâneos para um observador não são simultâneos para outro observador em movimento relativo.

Os observadores têm um conjunto de eventos simultâneos em torno deles que eles consideram como compor o instante presente. A relatividade da simultaneidade resultados em observadores que estão se movendo em relação à outra com diferentes conjuntos de eventos em seu instante presente.

O efeito líquido do universo de quatro dimensões é que os observadores que estão em movimento em relação a você parece ter coordenadas de tempo que se inclinam sobre na direção do movimento, e considerar as coisas para ser simultâneos que não são simultâneos para você. Comprimentos espaciais na direcção da viagem são encurtados, porque a ponta para cima e para baixo, em relação ao eixo do tempo na direcção da viagem, semelhante a uma inclinação ou de cisalhamento do espaço tridimensional.

Grande cuidado é necessário ao interpretar diagramas de espaço-tempo. Diagramas presentes dados em duas dimensões, e não pode mostrar fielmente como, por exemplo, um intervalo de espaço-tempo comprimento zero aparece.

A relatividade geral: uma olhada para a frente

Ao contrário de leis do movimento de Newton, a relatividade não é baseada em postulados dinâmicos. Ele não assume nada sobre o movimento ou forças. Em vez disso, ele lida com a natureza fundamental do espaço-tempo. Ele refere-se a descrever a geometria do fundo sobre o qual todos os fenómenos dinâmicos ter lugar. Em certo sentido, portanto, é uma meta-teoria, uma teoria que estabelece uma estrutura que todas as outras teorias deve seguir. Na verdade, a relatividade especial é apenas um caso especial. Assume-se que o espaço-tempo é plano. Ou seja, ele assume que a estrutura do espaço Minkowski eo tensor métrico Minkowski é constante por toda parte. Na relatividade geral , Einstein mostrou que isso não é verdade. A estrutura de espaço-tempo é modificado pela presença da matéria. Especificamente, a fórmula de distância dada acima não é mais válido geralmente exceto em espaço livre de massa. No entanto, apenas como uma superfície curva pode ser considerada plana no limite infinitesimal de cálculo, um espaço-tempo curvo pode ser considerado estável em pequena escala. Isto significa que a métrica de Minkowski escrito na forma diferencial é geralmente válido.

Diz-se que a métrica de Minkowski é válido localmente, mas ele não consegue dar uma medida de distância em longas distâncias. Não é válida a nível mundial. De facto, em geral, a relatividade si métrica global se torna dependente da distribuição de massa e varia no espaço. O problema central da relatividade geral é a de resolver o famoso Equações de campo de Einstein para uma determinada distribuição de massa e encontrar a fórmula de distância que se aplica nesse caso particular. Formulação espaço-tempo de Minkowski foi o trampolim conceitual para a relatividade geral. Sua fundamentalmente nova perspectiva permitiu não só o desenvolvimento da relatividade geral, mas também, em certa medida as teorias quânticas de campo .

Equivalência massa-energia: luz solar e bombas atômicas

Einstein mostrou que a massa é simplesmente uma outra forma de energia. A energia equivalente a restante massa m é mc ^2. Esta equivalência significa que a massa deve ser interconversíveis com outras formas de energia. Este é o princípio básico por trás de bombas atômicas e de produção de energia em reatores e as estrelas (como o Sol) nucleares.

Aplicações

Há uma percepção comum de que a física relativista não é necessária para fins práticos ou na vida cotidiana. Isso não é verdade. Sem os efeitos relativísticos, ouro olharia prateado, em vez de amarelo. Muitas tecnologias estão criticamente dependente física relativista:

• Tubos de raios catódicos,
• Os aceleradores de partículas,
• Sistema de Posicionamento Global (GPS) - embora isso realmente exige a teoria completa da relatividade geral

Os postulados da relatividade especial

Einstein desenvolveu a relatividade especial, com base em dois postulados:

• Primeiro postulado - Especial princípio da relatividade - As leis da física são as mesmas em todos sistemas de referência inerciais. Em outras palavras, não há referenciais inerciais privilegiados de referência.
• Segundo postulado - Invariance de c - A velocidade da luz em um vácuo é independente do movimento da luz da fonte.

A relatividade especial pode ser obtido a partir destes postulados, como foi feito por Einstein em 1905. postulados de Einstein ainda são aplicáveis na teoria moderna, mas a origem dos postulados é mais explícita. Foi mostrado acima que a existência de uma velocidade constante universal (à velocidade da luz) é uma consequência de modelar o universo como um espaço de quatro dimensões particular tendo certas propriedades específicas. O princípio de relatividade é um resultado da estrutura Minkowski ser preservada sob transformações de Lorentz, que são postulados para ser as transformações físicas de referenciais inerciais.