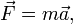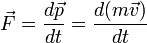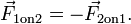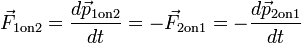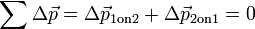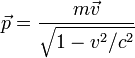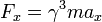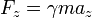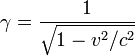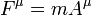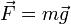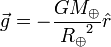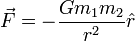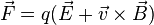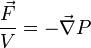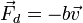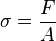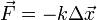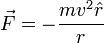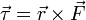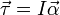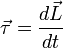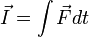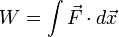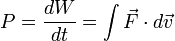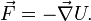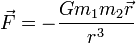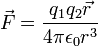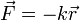Vigor
Informações de fundo
Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Patrocinar uma criança para fazer uma diferença real.
| Procurar vigor em Wiktionary, o dicionário livre. |
Em física , força é o que faz com que uma massa para acelerar e é experimentado como um empurrão ou um puxão. O vector soma de todas as forças que actuam sobre um corpo (conhecido como o força líquida ou força resultante) é proporcional à aceleração e a massa do corpo. Em um corpo estendido, força também pode causar rotação, deformação, ou uma mudança na pressão. Efeitos rotacionais são determinados pela binários, enquanto que a pressão de deformação e são determinados pela salienta que as forças de criar.
Força resultante é matematicamente idêntico ao momento taxa de variação da quantidade de movimento do corpo sobre a qual actua. Uma vez que o impulso é um vector quantidade (isto é, que tem tanto uma e magnitude direcção), a força também é uma grandeza vectorial.
O conceito de força tem sido utilizado em estática e dinâmica desde os tempos antigos. O que se sabe sobre as contribuições antigos até estática é geralmente dito que culminou com a obra de Arquimedes na Terceiro século antes de Cristo, que ainda faz parte da física moderna. Em contraste, de Aristóteles dinâmica incorporada mal-entendidos intuitivos do papel da força que acabaram por ser corrigidos no século 17 que culminou com a obra de Isaac Newton . Seguindo o desenvolvimento da mecânica quântica eo modelo padrão da física de partículas , é agora entendido que as forças associadas com as mudanças na dinâmica de partículas são a consequência de interações fundamentais que acompanham a emissão ou absorção de bósons. Em grandes escalas, as forças são percebidos de forma mais precisa atribuível ao curvatura espaço-tempo como explicada em Einstein 's Teoria da Relatividade Geral . Em a física moderna, apenas quatro interações fundamentais são conhecidos; por ordem decrescente de força, são eles: [força forte | forte]], eletromagnética , fraco, e gravitacional. física de partículas de alta energia observações em 1970 e 1980 confirmou que as forças fraca e eletromagnética são expressões de um sistema unificado interação eletrofraca.
Conceitos pré-newtonianos

Desde a antiguidade, o conceito de força foi reconhecido como parte integrante do funcionamento de cada um dos máquinas simples. O vantagem mecânica dada por uma máquina simples permitiu menos força para ser usado em troca de que a força que actua sobre uma distância maior. Análise das características de forças, como tal, em última análise, culminou com a obra de Arquimedes que era especialmente famoso para a formulação de um tratamento de forças flutuantes inerentes fluidos.
Philosophical desenvolvimento do conceito de uma força procedeu através do trabalho de Aristóteles . Em Cosmologia Aristotleian, o mundo natural realizada quatro elementos que existiam em "estado natural". Aristóteles acreditava que era o estado natural de objetos maciços em terra , como os elementos água e terra, para serem imóvel no chão e que tendeu para que estado se deixado sozinho. Ele distingue entre a tendência inata de objetos para encontrar o seu "lugar natural" (por exemplo, para os corpos pesados para cair), que levam a "movimento natural", eo movimento não natural ou forçada, o que exigiu a aplicação continuada de uma força. Esta teoria, com base na experiência cotidiana de como os objetos se movem, como a aplicação constante de uma força necessária para manter um carro em movimento, teve dificuldade conceitual representando o comportamento de projéteis, tais como o vôo de flechas.
Estas carências não seria totalmente explicado e corrigido até que o trabalho do século XVII de Galileo Galilei , que foi influenciado pela ideia medieval de que objetos em movimento forçado realizada uma força inata de ímpeto. Galileu construiu um experimento no qual as pedras e balas de canhão foram ambos rolaram uma inclinação para contestar a Teoria aristotélica de movimento no início do século 17 . Ele mostrou que os corpos foram aceleradas pela gravidade de uma forma que era independente de sua massa e argumentou que os objetos mantêm a sua velocidade a menos que actuado por uma força, por exemplo atrito.
Mecânica newtoniana
Isaac Newton é reconhecida como a primeira pessoa a argumentar explicitamente que uma força constante faz com que uma taxa constante de mudança ( derivada temporal) de impulso. Em essência, ele deu a primeira ea única definição, matemático da força - como o tempo derivado do momento: 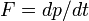 . Em 1687, Newton passou a publicar seu Philosophiae Naturalis Principia Mathematica , que utilizou conceitos de inércia, força e conservação para descrever o movimento de todos os objectos.
. Em 1687, Newton passou a publicar seu Philosophiae Naturalis Principia Mathematica , que utilizou conceitos de inércia, força e conservação para descrever o movimento de todos os objectos.

Em Principia Mathematica , Newton estabeleceu três leis de movimento que têm relevância direta para a forma como as forças são descritos na física.
A primeira lei de Newton
Primeira lei do movimento de Newton estabelece as condições necessárias para o equilíbrio e define o inércia relacionada com a massa de um objecto. No lugar da idéia aristotélica de "estados naturais", Newton propôs que ele foi a falta de força líquida que era o "estado natural" fundamental. Isto implica directamente que a condição de velocidade constante, seja zero ou diferente de zero, é o "estado natural" de todos os objectos em massa. Objetos continuam a mover-se em um estado de velocidade constante, a menos que influenciado por uma força externa desequilibrado. Como uma extensão do trabalho de Galileu, o conceito de inércia é inexoravelmente ligado ao conceito de velocidades relativas. Especificamente, em sistemas de dois corpos, é impossível determinar a qual o objecto é "em marcha" e que é objecto "em repouso"; é equivalente a alternar entre o que é chamado em física "inercial quadros de referência ".
O conceito de inércia pode ser mais generalizado para explicar a tendência de objectos para continuar em muitas formas diferentes de movimento constante, mesmo aqueles que não são estritamente velocidade constante. O momento de inércia do planeta Terra é o que fixa a constância do comprimento de um dia e o comprimento de um ano. Albert Einstein estendeu o princípio da inércia ainda mais quando ele explicou que os quadros de referência sujeitos a aceleração constante, tais como aqueles em queda livre em direção a um objeto gravitando, eram fisicamente equivalente a referenciais inerciais. É por isso que, por exemplo, os astronautas experiência ausência de peso quando em órbita de queda livre em torno da Terra, e por que as leis do movimento de Newton são mais facilmente discerníveis em tais ambientes. Se um astronauta coloca um objeto massivo no ar ao lado de si mesma, ela permanecerá estacionário em relação ao astronauta devido à sua inércia. Esta é a mesma coisa que ocorreria se o astronauta eo objeto maciço estavam no espaço intergaláctico com nenhuma força resultante da gravidade agindo em seu quadro de referência compartilhado. Este princípio da equivalência foi uma das bases fundamentais para o desenvolvimento de sua teoria da relatividade geral .
A segunda lei de Newton
A força é muitas vezes definida usando a segunda lei de Newton , que o produto de massa 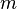 multiplicado pela aceleração
multiplicado pela aceleração 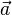 :
:
às vezes chamado de "segunda fórmula mais famosa da física". Newton nunca afirmou explicitamente o F = ma fórmula para o qual ele é muitas vezes creditado. A segunda lei de Newton é descrita em seu Principia Mathematica como um vector equação diferencial :
onde 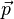 é a dinâmica do sistema. A força é a taxa de variação da quantidade de movimento ao longo do tempo. A aceleração é a taxa de variação da velocidade ao longo do tempo. Este resultado, que segue como uma consequência directa da ressalva na Primeira Lei de Newton, mostra que a crença aristotélica intuitiva que é necessária uma força resultante para manter um objeto em movimento com velocidade constante (portanto aceleração zero) é objetivamente errado e não apenas uma consequência de uma má escolha de definição.
é a dinâmica do sistema. A força é a taxa de variação da quantidade de movimento ao longo do tempo. A aceleração é a taxa de variação da velocidade ao longo do tempo. Este resultado, que segue como uma consequência directa da ressalva na Primeira Lei de Newton, mostra que a crença aristotélica intuitiva que é necessária uma força resultante para manter um objeto em movimento com velocidade constante (portanto aceleração zero) é objetivamente errado e não apenas uma consequência de uma má escolha de definição.
A utilização da segunda lei de Newton, em qualquer uma destas formas como uma definição da força tem sido menosprezado em alguns dos livros mais rigorosos, porque este remove todo o conteúdo empírica da lei. Na verdade, o 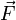 nesta equação representa a força líquida (soma vetorial); em equilíbrio este é zero por definição, mas as forças (equilibradas) estão presentes, no entanto. Em vez disso, a segunda lei de Newton afirma apenas a proporcionalidade de aceleração e de massa para forçar, cada um dos quais pode ser definida sem referência explícita às forças. Acelerações pode ser definido por meio de medições cinemáticas enquanto massa pode ser determinada através de, por exemplo, contando átomos. No entanto, enquanto a cinemática está bem descrita através análise referencial em física avançada, ainda existem questões profundas que permanecem, como o que é a definição adequada de massa. A relatividade geral oferece uma equivalência entre espaço-tempo e massa, mas falta uma teoria coerente de gravidade quântica, não está claro como ou se essa conexão é relevante em microscales. Com um pouco mais justificação, a segunda lei de Newton pode ser tomado como uma definição quantitativa de massa escrevendo a lei como uma igualdade, são fixadas as unidades relativas de força e de massa.
nesta equação representa a força líquida (soma vetorial); em equilíbrio este é zero por definição, mas as forças (equilibradas) estão presentes, no entanto. Em vez disso, a segunda lei de Newton afirma apenas a proporcionalidade de aceleração e de massa para forçar, cada um dos quais pode ser definida sem referência explícita às forças. Acelerações pode ser definido por meio de medições cinemáticas enquanto massa pode ser determinada através de, por exemplo, contando átomos. No entanto, enquanto a cinemática está bem descrita através análise referencial em física avançada, ainda existem questões profundas que permanecem, como o que é a definição adequada de massa. A relatividade geral oferece uma equivalência entre espaço-tempo e massa, mas falta uma teoria coerente de gravidade quântica, não está claro como ou se essa conexão é relevante em microscales. Com um pouco mais justificação, a segunda lei de Newton pode ser tomado como uma definição quantitativa de massa escrevendo a lei como uma igualdade, são fixadas as unidades relativas de força e de massa.
A definição de força é por vezes considerado como problemático, uma vez que deve, ou em última análise, ser encaminhado para a nossa compreensão intuitiva de nossas percepções diretas, ou ser definido implicitamente através de um conjunto de fórmulas matemáticas auto-consistente. Notáveis físicos, filósofos e matemáticos que têm procurado uma definição mais explícita incluem Ernst Mach, Clifford Truesdell e Walter Noll.
Dado o sucesso empírico da lei de Newton, muitas vezes é utilizada para medir a força de forças (por exemplo, usando órbitas astronômicas para determinar forças gravitacionais). No entanto, a força e as quantidades utilizadas para medi-lo permanecer conceitos distintos.
'Quando uma resultante actua sobre um objecto de uma massa constante, uma aceleração irá resultar com o produto da sua massa e aceleração igual à força resultante, a direcção da aceleração estar na mesma direcção que a força resultante. F = ma '
A terceira lei de Newton
A terceira lei de Newton é um resultado da aplicação de simetria para situações em que as forças podem ser atribuídos à presença de diferentes objectos. Para quaisquer dois objetos (chamá-los 1 e 2), a terceira lei de Newton afirma que
Esta lei implica que as forças ocorrem sempre em pares ação-reação. Qualquer força que é aplicada para se opor 1, devido à acção do objecto 2 é automaticamente acompanhada por uma força aplicada ao objecto 2, devido à acção do objecto 1. Se um objecto e objecto 2 são consideradas estar no mesmo sistema, em seguida, o força total no sistema devido às interações entre objetos 1 e 2 é zero desde
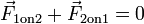 .
.
Isto significa que não é possível criar sistemas forças internas que são desequilibradas. No entanto, se os objectos 1 e 2 são considerados em sistemas separados, em seguida, os dois sistemas de cada vai experimentar uma força assimétrica e acelerar em relação um ao outro de acordo com a segunda lei de Newton.
Combinando segunda e terceira lei de Newton, é possível demonstrar que a quantidade de movimento linear de um sistema é conservada . Uso
e integrar com respeito ao tempo, a equação:
é obtido. Para um sistema que inclui objetos 1 e 2,
que é a conservação do momento linear. Generalizando este para um sistema de um número arbitrário de partículas é simples. Isto mostra que a troca dinâmica entre objectos constituintes não irá afectar a quantidade de movimento de um sistema líquido. Em geral, desde que todas as forças são devidas à interacção dos objectos em massa, é possível definir um sistema de impulso de modo a que líquido não se perde nem adquirida.
'Se o corpo A exerce uma força F no corpo B, em seguida, o corpo B exerce uma força de -F (de igual tamanho, mas no sentido oposto) no corpo A.'
Descrições
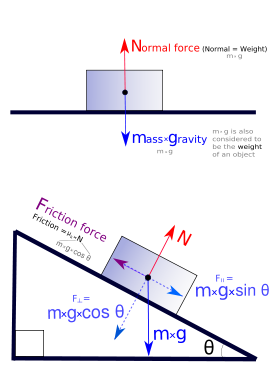
Forças pode ser directamente percebido como empurra ou puxa; isso pode fornecer um quadro intuitivo para descrever forças. Tal como acontece com outros conceitos físicos (por exemplo, temperatura ), a noção intuitiva é quantificado usando definições operacionais que são consistentes com a percepção direta, mas são mais precisos (ver a seção sobre a mecânica newtoniana para como isso é feito ). Historicamente, as forças foram quantitativamente primeiro investigada em condições de equilíbrio estático onde várias forças anulam-se mutuamente. Tais experiências provam as propriedades cruciais que as forças são aditivos vetor quantidades: eles têm e magnitude direção. Quando duas forças atuam sobre um objeto, a força resultante, a resultante, é a soma vetorial das forças originais. Isso é chamado de princípio da superposição. A magnitude da resultante varia a partir da diferença das magnitudes das duas forças a sua soma, dependendo do ângulo entre as suas linhas de acção. A força resultante pode ser determinada seguindo o regra paralelogramo de adição de vectores: a adição de dois vectores representados por lados de um paralelogramo, dá um vector resultante equivalente, que é igual em magnitude e direcção transversal à do paralelogramo.
Diagramas de corpo livre pode ser utilizado como um meio conveniente para manter o controle das forças que actuam no sistema. Idealmente, estes diagramas são desenhados com os ângulos e as magnitudes relativas dos vectores de força de conservas, de modo que a adição de vectores gráfica pode ser feito para determinar a resultante.
Para além de serem adicionadas, as forças podem também ser resolvidos em componentes independentes na ângulos rectos entre si. A nordeste força horizontal apontando, portanto, pode ser dividida em duas forças, uma norte apontando, e um apontador leste. Resumindo estas forças componentes utilizando a adição de vectores produz a força inicial. Resolvendo vetores de força em componentes de um conjunto de vetores de base é muitas vezes uma forma mais limpa matematicamente para descrever as forças que usando magnitudes e direções. Isto porque, para componentes ortogonais, os componentes do vector soma são determinados exclusivamente pela adição escalar dos componentes dos vectores individuais. Componentes ortogonais são independentes um do outro; forças que actuam em noventa graus entre si não têm qualquer efeito um sobre o outro. A escolha de um conjunto de vectores de base ortogonais é muitas vezes feito considerando-se que conjunto de vetores de base vai fazer a matemática mais conveniente. A escolha de um vector base que é na mesma direcção que uma das forças é desejável, uma vez que a força teria então apenas um componente não zero. Vectores de força podem também ser tridimensional, com o terceiro componente em ângulo recto com os dois outros componentes.
Equilíbrios
O equilíbrio ocorre quando a força resultante actuando sobre um objecto é igual a zero (isto é, o vector soma de todas as forças é zero). Existem dois tipos de equilíbrio: equilíbrio estático e equilíbrio dinâmico.
Equilíbrio estático
Equilíbrio estático foi entendido bem antes da invenção da mecânica clássica. Objetos que estão em repouso tem força resultante nula agindo sobre eles.
O caso mais simples de equilíbrio estático ocorre quando duas forças são iguais em grandeza, mas opostas em sentido. Por exemplo, qualquer objeto em uma superfície plana é puxado (atraiu) para baixo em direção ao centro da Terra pela força da gravidade. Ao mesmo tempo, as forças de superfície resistir à força descendente com igual força para cima (o chamado força normal) e resultar no objecto tendo uma diferente de zero peso. A situação é um zero força líquida e sem aceleração.
Empurrando contra um objeto em uma superfície de atrito pode resultar em uma situação em que o objeto não se move porque a força aplicada é a oposição de fricção estática, gerada entre o objecto e a superfície da mesa. Para uma situação sem movimento, a força de atrito estático equilibra exactamente a força aplicada que resulta em ausência de aceleração. Os aumentos de atrito estático ou diminui em resposta à força aplicada, até um limite superior determinado pelas características do contacto entre a superfície e o objecto.
Um equilíbrio estático entre duas forças é a forma mais habitual de forças de medição, utilizando dispositivos simples tais como balanças e saldos da mola. Por exemplo, um objecto suspenso num verticais balança de mola experimenta a força da gravidade que actua sobre o objecto equilibrada por uma força aplicada pelo "força de reacção da mola", que é igual ao peso do objecto. Usando essas ferramentas, algumas leis de força quantitativos foram descobertas: que a força da gravidade é proporcional ao volume de objetos de constante densidade (amplamente exploradas por milênios para definir pesos padrão); «Princípio de flutuabilidade; Archimedes Archimedes 'análise da alavanca; A lei de Boyle por pressão do gás; e A lei de Hooke de molas. Estes foram todos formulada e experimentalmente verificada antes de Isaac Newton expôs suas três leis do movimento .
Equilíbrio dinâmico

Equilíbrio dinâmico foi primeiramente descrita por Galileu , que notou que certos pressupostos da física aristotélica foram contraditas por observações e lógica . Galileu percebeu que Além velocidade simples exige que o conceito de uma "absoluta "não existia. Galileo concluiu que o movimento em uma constante quadro resto velocidade estava completamente equivalente ao resto. Este era contrário à noção de um de Aristóteles "estado natural" de descanso que objetos massivos naturalmente abordado. experimentos simples mostraram que a compreensão de Galileo da equivalência de velocidade constante e descanso para ser correto. Por exemplo, se um marinheiro caiu uma bala de canhão do ninho do corvo de um navio em movimento a uma velocidade constante, física aristotélica teria a bala de canhão cair em linha reta, enquanto o navio se moveu sob ele. Assim, um universo aristotélico, a bala de canhão caindo iria pousar atrás do pé do mastro de um navio em movimento. No entanto, quando esta experiência é realmente realizado, a bala de canhão sempre cai no pé do mastro, como se a bala de canhão sabe para viajar com o navio apesar de ser separado dela. Uma vez que não existe qualquer força horizontal para a frente a ser aplicada sobre a bala à medida que cai, a única conclusão que resta é o potente continua a mover-se com a mesma velocidade que o barco enquanto cai. Assim, nenhuma força é necessária para manter o canhão movendo-se a velocidade de deslocamento constante.
Além disso, qualquer objeto que viaja a uma velocidade constante devem ser sujeitos a zero força líquida (força resultante). Esta é a definição de equilíbrio dinâmico: quando todas as forças numa balança objecto mas ainda se move a uma velocidade constante.
Um exemplo simples de equilíbrio dinâmico ocorre no movimento de velocidade constante através de uma superfície com atrito cinético. Em tal situação, é aplicada uma força na direcção de movimento, a força de atrito cinética exactamente opõe à força aplicada. Isto resulta numa força líquida de zero, mas uma vez que o objecto iniciado com uma velocidade diferente de zero, que continua a mover-se com uma velocidade diferente de zero. Aristóteles mal interpretado este movimento como sendo causada pela força aplicada. No entanto, quando a fricção cinética é tomada em consideração, é claro que não existe qualquer força resultante causando movimento de velocidade constante.
Diagramas de Feynman
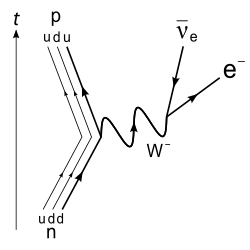
Forças e a aceleração de partículas em modernas física de partículas acontecer durante a troca de bósons. Com o desenvolvimento da teoria quântica de campos e relatividade geral , percebeu-se que "força" é um conceito redundante decorrentes da conservação do momento ( 4-momentum na relatividade e dinâmica do em partículas virtuais Eletrodinâmica Quântica). A conservação do momento, desde Teorema de Noether, pode ser derivada diretamente da de simetria espacial e por isso é geralmente considerada mais fundamental que o conceito de uma força. Assim, o actualmente conhecido forças fundamentais são considerados mais exacta para ser " interações fundamentais ". Enquanto as descrições matemáticas sofisticadas são necessários para prever, em pormenor, a natureza de tais interacções, não há uma maneira conceptualmente simples para descrever estas interacções através da utilização de diagramas de Feynman. Em um diagrama de Feynman, cada partícula de matéria é representado como uma linha reta (ver linha do mundo) viajando através do tempo que normalmente aumenta para cima ou para a direita no diagrama. Matéria e anti-matéria partículas são idênticas exceto quanto ao sentido da propagação através do diagrama de Feynman. Linhas mundo das partículas se cruzam em vértices de interacção, e o diagrama de Feynman representa qualquer força resultante de uma interacção como ocorrendo no vértice com uma mudança instantânea associado na direcção das linhas de mundo partículas. Bósons são emitidos para longe a partir do vértice como linhas onduladas (semelhantes às ondas) e, no caso de troca virtual de partículas, são absorvidos por um vértice adjacente. Quando os bósons são representados em um diagrama de Feynman como existente entre duas partículas que interagem, isso representa uma força repulsiva. Quando os bósons são representados em um diagrama de Feynman como existente em torno das duas partículas que interagem, isso representa uma força atrativa.
O utilitário de diagramas de Feynman é que outros tipos de fenômenos físicos que fazem parte do quadro geral de interações fundamentais, mas são conceitualmente separado de forças também pode ser descrito usando as mesmas regras. Por exemplo, um diagrama de Feynman pode descrever em detalhes sucinta como um nêutron decai em um elétron , protão , e neutrino: uma interacção mediada pela mesma Higgs calibre que é responsável pela força nuclear fraca. Embora o diagrama de Feynman para esta interacção tem características semelhantes a uma interacção repulsiva, o decaimento é mais complicado do que uma "força de repulsa" simples.
A relatividade especial
Na teoria de relatividade especial de massa e energia são equivalentes (tal como pode ser visto através do cálculo do trabalho necessário para acelerar um corpo). Quando a velocidade de um objeto aumenta o mesmo acontece com a sua energia e, consequentemente, o seu equivalente em massa (inércia). Exige, portanto, mais força para acelerá-lo a mesma quantidade do que ele fez a uma velocidade mais baixa. A definição 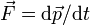 permanece válida. Mas, para ser conservado, o momento deve ser redefinido como:
permanece válida. Mas, para ser conservado, o momento deve ser redefinido como:
onde
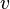 é a velocidade e
é a velocidade e
 é a velocidade da luz .
é a velocidade da luz .
A expressão relativista relativa força e aceleração de uma partícula não-zero massa de repouso 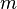 movendo-se no
movendo-se no 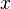 direção é:
direção é:
onde o Fator de Lorentz
Aqui uma força constante não produz uma aceleração constante, mas uma aceleração sempre diminuindo à medida que o objecto se aproxima da velocidade da luz. Note que 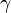 é indefinido para um objecto com um diferente de zero descansar em massa na velocidade da luz, ea teoria produz nenhuma previsão a essa velocidade.
é indefinido para um objecto com um diferente de zero descansar em massa na velocidade da luz, ea teoria produz nenhuma previsão a essa velocidade.
No entanto pode-se restaurar a forma de
para uso na relatividade através da utilização de quatro vectores. Esta relação é correta quando na relatividade 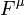 é o quatro força, m é a massa invariante, e
é o quatro força, m é a massa invariante, e  é o quatro aceleração.
é o quatro aceleração.
Modelos Fundamentais
Todas as forças do Universo são todos baseados em quatro forças fundamentais. As forças fortes e fracos agir apenas em distâncias muito curtas, e são responsáveis por manter determinados nucleons e compostos núcleos juntos. A força eletromagnética atua entre cargas elétricas ea força gravitacional actua entre massas . Todas as outras forças são baseados na existência de quatro interacções fundamentais. Por exemplo, o atrito é uma manifestação da força electromagnética que actua entre os átomos de dois superfícies, bem como a exclusão Pauli, que não permite átomos de passar através de cada outro. As forças em modelada por molas A lei de Hooke também são o resultado de forças eletromagnéticas eo princípio de exclusão agindo em conjunto para voltar o objeto à sua posição de equilíbrio. Forças centrífugas são as forças de aceleração que surgem simplesmente da aceleração da rotação quadros de referência.
O moderno vista da mecânica quântica dos primeiros três forças fundamentais (todos, exceto gravidade) é que partículas de matéria ( férmions) não interagem diretamente uns com os outros, mas sim pela troca de partículas virtuais chamados bósons.
É um equívoco comum atribuir a dureza e rigidez de matéria sólida para a repulsão de cargas como, sob a influência da força electromagnética. No entanto, estas características realmente resultam da Exclusão de Pauli Princípio. Desde elétrons são fermiones, que não pode ocupar a mesma estado da mecânica quântica como outros elétrons. Quando os elétrons em um material são densamente juntos, não há o suficiente menor energia estados quânticos para todos eles, por isso alguns deles devem estar em estados de energia mais altos. Isso significa que é preciso energia para embalá-los juntos. Embora este efeito manifesta-se macroscopicamente como uma "força" estrutural, é tecnicamente apenas o resultado da existência de um conjunto finito de estados de electrões.
Gravidade
O que hoje chamamos gravidade não foi identificada como uma força universal até que o trabalho de Isaac Newton. Antes de Newton, a tendência para os objectos a cair em direção a Terra não era entendido como estar relacionado com os movimentos de objetos celestiais. Galileo foi fundamental para descrever as características de queda de objectos, determinando que a aceleração de cada corpo em de queda livre foi constante e independente da massa do objecto. Hoje em dia, este aceleração devida à gravidade na superfície da Terra é geralmente designado como 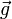 e tem uma magnitude de cerca de 9,81 metros por segundo quadrado (esta medição é feita a partir do nível do mar, e podem variar dependendo da localização), e aponta para o centro da Terra. Essa observação significa que a força da gravidade sobre um objecto na superfície da Terra é directamente proporcional à massa do objecto. Assim, um objecto que tem uma massa de
e tem uma magnitude de cerca de 9,81 metros por segundo quadrado (esta medição é feita a partir do nível do mar, e podem variar dependendo da localização), e aponta para o centro da Terra. Essa observação significa que a força da gravidade sobre um objecto na superfície da Terra é directamente proporcional à massa do objecto. Assim, um objecto que tem uma massa de 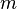 experimentará uma força:
experimentará uma força:
Em queda livre, esta força é sem oposição e, portanto, a força resultante sobre o objeto é a força da gravidade. Para objetos não em queda livre, a força da gravidade é a oposição do peso do objecto. Por exemplo, uma pessoa em pé no chão experimenta força líquida igual a zero, uma vez que a força da gravidade é em relação ao peso da pessoa que se manifesta por uma força normal exercida sobre a pessoa pelo solo.
A contribuição de Newton à teoria gravitacional era unificar os movimentos dos corpos celestes, que Aristóteles tinha assumido estavam em um estado natural de movimento constante, com movimento de queda observada na Terra. Ele propôs uma lei da gravidade que poderia explicar os movimentos celestes que haviam sido descritos anteriormente usando leis de Kepler do movimento planetário .
Newton percebeu que os efeitos da gravidade pode ser observada em diferentes formas em distâncias maiores. Em particular, Newton determinou que a aceleração da Lua em torno da Terra pode ser atribuído à mesma força de gravidade se a aceleração devida à gravidade diminuiu como um lei do inverso do quadrado. Além disso, Newton percebeu que a massa do objeto gravitando afetou diretamente a aceleração da gravidade. Combinando estas ideias dá uma fórmula que relaciona a massa da Terra ( 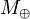 ), O raio da Terra (
), O raio da Terra ( 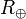 ) Para a aceleração devida à gravidade:
) Para a aceleração devida à gravidade:
em que o vector de direcção é dada pela 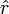 o qual é a unidade vector dirigido para fora a partir do centro da Terra.
o qual é a unidade vector dirigido para fora a partir do centro da Terra.
Nesta equação, uma constante dimensional 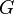 é usado para descrever a força relativa da gravidade. Esta constante tem vindo a ser conhecido como Gravitação Universal de Newton constante, embora fosse de um valor desconhecido na vida de Newton. Não até 1798 era Henry Cavendish capaz de fazer a primeira medição de
é usado para descrever a força relativa da gravidade. Esta constante tem vindo a ser conhecido como Gravitação Universal de Newton constante, embora fosse de um valor desconhecido na vida de Newton. Não até 1798 era Henry Cavendish capaz de fazer a primeira medição de 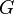 usando um balança de torção; este foi amplamente divulgado na imprensa como uma medida da massa da Terra, uma vez sabendo o
usando um balança de torção; este foi amplamente divulgado na imprensa como uma medida da massa da Terra, uma vez sabendo o 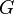 pode permitir uma para resolver para a massa da Terra dada a equação acima. Newton, no entanto, percebeu que desde que todos os corpos celestes seguiram as mesmas leis do movimento , sua lei da gravidade tinha de ser universal. Sucintamente, Lei de Newton da Gravitação entre dois corpos maciços é
pode permitir uma para resolver para a massa da Terra dada a equação acima. Newton, no entanto, percebeu que desde que todos os corpos celestes seguiram as mesmas leis do movimento , sua lei da gravidade tinha de ser universal. Sucintamente, Lei de Newton da Gravitação entre dois corpos maciços é
onde 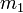 é a massa do primeiro objecto e
é a massa do primeiro objecto e 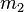 é a massa do segundo objecto.
é a massa do segundo objecto.
Esta fórmula foi poderoso o suficiente para ficar como a base para todas as descrições subsequentes de movimento dentro do sistema solar até o século XX. Durante esse tempo, métodos sofisticados de análise de perturbação foram inventados para calcular os desvios de órbitas devido à influência de vários corpos em um planeta , lua , cometa ou asteróide . Estas técnicas são tão poderosa que pode ser utilizada para prever com precisão o movimento dos corpos celestes para uma precisão arbitrária, em qualquer comprimento de tempo no futuro. O formalismo foi exacta suficiente para permitir matemáticos para prever a existência do planeta Neptuno antes de ter sido observada.
Foi apenas a órbita do planeta Mercúrio que a Lei da Gravitação de Newton parecia não explicar totalmente. Alguns astrofísicos previu a existência de outro planeta ( Vulcan) que explicaria as discrepâncias; No entanto, apesar de algumas indicações iniciais, tal planeta poderia ser encontrado. Quando Albert Einstein finalmente formulou sua teoria da relatividade geral (GR), ele voltou sua atenção para o problema da órbita de Mercúrio e descobriram que sua teoria acrescentado uma correção que poderia explicar a discrepância. Esta foi a primeira vez que a teoria da gravidade de Newton tinha sido mostrado para ser menos do que uma alternativa correcta.
Desde então, e até agora, a relatividade geral tem sido reconhecida como a teoria que melhor explica a gravidade. No GR, a gravitação não é visto como uma força, mas sim, objetos que se movem livremente em campos gravitacionais viajar sob a sua própria inércia em linhas retas através curvado espaço-tempo - definidos como o caminho mais curto espaço de tempo entre dois eventos espaço-tempo. Do ponto de vista do objeto, todo o movimento ocorre como se não houvesse gravidade que seja. É só quando observando o movimento em um sentido global que a curvatura do espaço-tempo pode ser observado e a força é inferida a partir trajetória curva do objeto. Assim, o caminho de linha recta no espaço-tempo é visto como uma linha curva no espaço, e chama-se a balístico trajectória do objecto. Por exemplo, um basquete jogado a partir do solo se move em um parábola, como é num campo gravitacional uniforme. Sua trajetória espaço-tempo (quando a dimensão ct extra é adicionado) é quase uma linha reta, ligeiramente curvo (com a raio de curvatura da ordem de alguns anos-luz). A derivada temporal do momento em mudança do corpo é o que nós rotulamos como "força gravitacional".
Forças eletromagnéticas
Em 1784 Charles Coulomb descobriu a lei do inverso do quadrado da interação entre cargas elétricas utilizando uma balança de torção; esta foi a segunda força fundamental. As forças fracas e fortes foram descobertos no século 20 através do desenvolvimento de física nuclear .
A força eletrostática foi descrita pela primeira vez em 1784 por Coulomb como uma força que existia intrinsecamente entre duas acusações . As propriedades da força electrostática que eram variados como uma lei inversa da raiz quadrada dirigida na direcção radial , foi atraente e repulsivo (houve intrínseca polaridade), foi independente da massa dos objetos carregados, e seguido o direito de sobreposição. Unificando todas essas observações em uma declaração sucinta ficou conhecida como a Lei de Coulomb .
Matemáticos posteriores e físicos encontraram a construção do campo eléctrico a ser útil para determinar a força electrostática sobre uma carga eléctrica em qualquer ponto no espaço. Com base na Lei de Coulomb, conhecendo as características do campo elétrico em um determinado espaço é equivalente a saber o que a força eletrostática aplicada em uma " carga de teste "é.
Enquanto isso, o conhecimento foi desenvolvido da força de Lorentz de magnetismo , a força que existe entre dois correntes elétricas. Ele tem o mesmo caráter matemático como a Lei de Coulomb com a ressalva de que, como correntes de atrair e repelir ao contrário de correntes. Semelhante ao campo eléctrico, o campo magnético pode ser utilizado para determinar a força magnética sobre uma corrente eléctrica em qualquer ponto no espaço. Combinando a definição de corrente eléctrica como a taxa de tempo de mudança de carga eléctrica produz uma lei de multiplicação vector chamado Lei de Lorentz, que determina a força sobre uma carga em movimento num campo magnético.
Assim, uma teoria completa da força electromagnética com uma carga pode ser escrito como uma soma da força electrostática (devido ao campo eléctrico) e a força magnética (devido ao campo magnético). Totalmente afirmou, esta é a lei:
onde 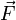 é a força electromagnética,
é a força electromagnética,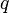 é a magnitude da carga da partícula,
é a magnitude da carga da partícula,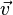 é avelocidadeda partícula,
é avelocidadeda partícula,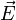 é o do campo eléctrico, e
é o do campo eléctrico, e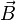 é o campo magnético.
é o campo magnético.
A origem de campos elétricos e magnéticos não seria totalmente explicado até 1864, quando James Clerk Maxwell unificou uma série de teorias anteriores em um conjunto sucinto de quatro equações. Estes " Equações de Maxwell "descrito plenamente as fontes de campos como sendo estacionário e cargas em movimento, e as interações dos próprios campos. Isto levou Maxwell para descobrir que os campos eléctricos e magnéticos pode ser "auto-geração" através de uma onda que viajava a uma velocidade que ele calculada como sendo a velocidade da luz . Essa percepção uniu os campos emergentes da teoria eletromagnética com óptica e levou diretamente para uma descrição completa do espectro eletromagnético.
No entanto, a tentativa de conciliar a teoria eletromagnética com duas observações, o efeito fotoelétrico, e a inexistência da catástrofe ultravioleta, mostrou-se problemático. Através do trabalho de físicos teóricos principais, uma nova teoria do eletromagnetismo foi desenvolvida utilizando a mecânica quântica . Esta modificação final a teoria eletromagnética levou a eletrodinâmica quântica (QED ou), que descreve totalmente todos os fenômenos eletromagnéticos como sendo mediada por partículas onda conhecidas como fótons . Em QED, os fótons são a partícula de troca fundamental que descreve todas as interações relacionadas ao eletromagnetismo, incluindo a força eletromagnética.
As forças nucleares
Há duas "forças nucleares", que hoje são geralmente descritos como interações que ocorrem em teorias quânticas dafísica de partículas. O força nuclear forte é a força responsável pela integridade estrutural denúcleos atômicos, enquanto aforça nuclear fraca é responsável pela deterioração de certosnucleons emléptons e outros tipos dehádrons.
A força forte é entendida hoje para representar as interações entre quarks e glúons, conforme detalhado pela teoria da cromodinâmica quântica (QCD). A força forte é a força fundamental mediada por glúons, agindo sobre quarks , antiquarks e os próprios glúons. A interação forte é a mais poderosa das quatro forças fundamentais.
A força forte só age diretamente sobre partículas elementares. No entanto, um residual da força é observada entre hádrons (o exemplo mais conhecido sendo a força que age entre nucleons em núcleos atômicos) como as força nuclear. Aqui as fortes força atua indiretamente, transmitida como glúons que fazem parte do pi virtuais e de Rho mésons que classicamente transmitem a força nuclear (ver este tópico para mais). O fracasso de muitas pesquisas para quarks livres mostrou que as partículas elementares não são afetadas diretamente observáveis. Este fenômeno é chamado cor confinamento.
A força fraca é devido à troca dos pesados bósons W e Z. Seu efeito mais conhecido é decaimento beta (de nêutrons em núcleos atômicos ) e do associado radioactividade. A palavra "fraco" deriva do fato de que a força do campo é cerca de 10 13 vezes menor do que a da força forte. Ainda assim, é mais forte do que a gravidade em distâncias curtas. Um consistente teoria eletrofraco também tem sido desenvolvida, que mostra que as forças electromagnéticas e a força fraca são indistinguíveis a temperaturas em excesso de cerca de 10 15 Kelvin . Tais temperaturas foram sondados em modernos aceleradores de partículas e mostrar as condições do universo nos primeiros momentos do Big Bang .
Modelos não-fundamentais
Algumas forças podem ser modelados, fazendo simplificadoras suposições sobre as condições físicas. Em tais situações, modelos idealizados pode ser utilizado para obter uma visão física.
Força normal

A força normal é a força que actua superfície normal à superfície de interface entre dois objectos. A força normal, por exemplo, é responsável pela integridade estrutural das tabelas e pisos, bem como sendo a força que responde sempre que uma força externa empurra sobre um objecto sólido. Um exemplo da força normal de acção é a força de impacto de um objecto colidir com uma superfície imóvel. Esta força é proporcional ao quadrado da velocidade desse objeto devido à conservação de energia e do teorema de energia trabalho quando aplicado a completamente colisões inelásticas.
Fricção
O atrito é uma força de superfície que se opõe ao movimento. A força de atrito está diretamente relacionada com a força normal que atua para manter dois objetos sólidos separados no ponto de contato. Existem duas grandes classificações das forças de atrito: atrito estático e atrito cinético.
A força de atrito estático (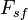 ) vai opor-se exactamente as forças aplicadas a um corpo paralelo a uma superfície de contacto até ao limite indicado pelocoeficiente de atrito estático (
) vai opor-se exactamente as forças aplicadas a um corpo paralelo a uma superfície de contacto até ao limite indicado pelocoeficiente de atrito estático (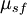 ) multiplicada pela força normal (
) multiplicada pela força normal (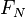 ).Por outras palavras, a magnitude da força de atrito estático da satisfaz desigualdade:
).Por outras palavras, a magnitude da força de atrito estático da satisfaz desigualdade:
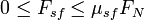 .
.
A força de atrito cinético ( 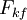 ) é independente de ambas as forças aplicadas e o movimento do objecto. Deste modo, a magnitude da força é igual
) é independente de ambas as forças aplicadas e o movimento do objecto. Deste modo, a magnitude da força é igual
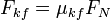 ,
,
onde 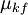 é o coeficiente de atrito cinético. Para a maioria das interfaces de superfície, o coeficiente de atrito cinético é menor do que o coeficiente de atrito estático.
é o coeficiente de atrito cinético. Para a maioria das interfaces de superfície, o coeficiente de atrito cinético é menor do que o coeficiente de atrito estático.
Mecânica do contínuo
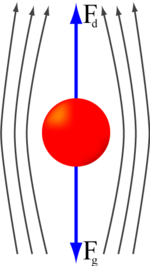
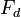 ) associada com a resistência do ar torna-se igual em magnitude ao da força da gravidade sobre um objecto em queda (
) associada com a resistência do ar torna-se igual em magnitude ao da força da gravidade sobre um objecto em queda ( ), o objectivo atinge um estado deequilíbrio dinâmicoàvelocidade terminal.
), o objectivo atinge um estado deequilíbrio dinâmicoàvelocidade terminal.Em estendidosfluidos, as diferenças depressão em resultado forças ser dirigida ao longo da pressão dosgradientes da seguinte forma:
onde 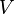 é o volume do objecto, em que o fluido e
é o volume do objecto, em que o fluido e 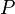 é o função escalar que descreve a pressão em todos os locais no espaço. Gradientes de pressão e diferenciais resultar na força de empuxo para fluidos suspensas em campos gravitacionais, ventos em ciência atmosférica, eo elevador associada a aerodinâmica e voo.
é o função escalar que descreve a pressão em todos os locais no espaço. Gradientes de pressão e diferenciais resultar na força de empuxo para fluidos suspensas em campos gravitacionais, ventos em ciência atmosférica, eo elevador associada a aerodinâmica e voo.
Um exemplo específico de um tal força que está associado coma pressão dinâmica é a resistência do fluido: uma força corpo que resiste ao movimento de um objecto por meio de um fluido, devido à viscosidade.Para o chamado "arrasto de Stokes "a força é aproximadamente proporcional à velocidade, mas em direção oposta:
onde:
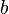 é uma constante que depende das propriedades do fluido e as dimensões do objecto (normalmente aárea de secção transversal), e
é uma constante que depende das propriedades do fluido e as dimensões do objecto (normalmente aárea de secção transversal), e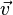 representa a velocidade do objecto.
representa a velocidade do objecto.
Mais formalmente, as forças emmecânica do contínuo estão totalmente desribed por umestressetensor com termos que são definidos como rougly
onde 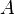 é a área da secção transversal relevante para o volume para o qual a tensão tensor está a ser calculado. Este formalismo inclui termos de pressão associadas às forças que agem normais para a área de corte transversal (as diagonais da matriz do tensor), bem como condições de corte associadas às forças que actuam paralelamente à área de secção transversal (os elementos fora da diagonal). O tensor de estresse é responsável por forças que causam todos deformações incluindo também tensões de tração e compressão.
é a área da secção transversal relevante para o volume para o qual a tensão tensor está a ser calculado. Este formalismo inclui termos de pressão associadas às forças que agem normais para a área de corte transversal (as diagonais da matriz do tensor), bem como condições de corte associadas às forças que actuam paralelamente à área de secção transversal (os elementos fora da diagonal). O tensor de estresse é responsável por forças que causam todos deformações incluindo também tensões de tração e compressão.
Tensão
Forças de tensão pode ser idealizada usando cordas que são ideais sem massa, sem atrito, inquebrável, e não extensível. Eles podem ser combinados com ideais roldanas que permitem cordas ideais para mudar direção física. Cordas ideais transmitir forças de tensão instantaneamente em pares ação-reação para que se dois objetos são conectados por uma corda ideal, qualquer força direcionada ao longo da cadeia, o primeiro objeto é acompanhado por uma força dirigida ao longo da corda na direção oposta pelo segundo objeto . Ao ligar a mesma cadeia várias vezes para o mesmo objecto, através da utilização de uma configuração que utiliza roldanas móveis, a força de tensão sobre uma carga pode ser multiplicado. Para cada cadeia que atua sobre uma carga, um outro fator da força de tensão na corda age sobre a carga. No entanto, apesar de tais máquinas para permitir um aumento da força, existe um aumento correspondente no comprimento de cadeia que tem de ser deslocado, a fim de mover a carga. Estes efeitos em tandem resultar em última análise, na conservação da energia mecânica desde o trabalho realizado sobre a carga é o mesmo, não importa o quão complicado a máquina.
Força elástica

Uma força elástica atua para retornar uma mola para seu comprimento natural. Um mola ideal é tida como sem massa, sem atrito, inquebrável, e infinitamente elástica. Tais molas exercem forças que empurram quando contratada, ou puxar quando estendida, em proporção ao deslocamento da primavera de sua posição de equilíbrio. Esta relação linear foi descrito por Robert Hooke, em 1676, para o qual . A lei de Hooke é nomeado Se 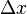 é o deslocamento, a força exercida por uma mola ideal é igual a:
é o deslocamento, a força exercida por uma mola ideal é igual a:
onde 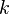 é a constante da mola (força ou constante), que é específica da mola. O sinal negativo contribui para a tendência de a força elástica para actuar em oposição à carga aplicada.
é a constante da mola (força ou constante), que é específica da mola. O sinal negativo contribui para a tendência de a força elástica para actuar em oposição à carga aplicada.
Força centrípeta
Para acelerar um objecto em movimento circular, a força desequilibrada agindo sobre o objecto é igual
onde 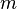 é a massa do objecto,
é a massa do objecto, 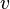 é a velocidade do objecto e
é a velocidade do objecto e  é a distância ao centro da trajectória circular e
é a distância ao centro da trajectória circular e 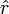 é o unidade vector que aponta no sentido radial para fora a partir do centro. Isto significa que a força centrípeta desequilibrada sentida por qualquer objecto é sempre dirigida para o centro da trajectória curva. Tais forças actuam perpendicularmente ao vector de velocidade associados com o movimento de um objecto, e, portanto, não alteram a velocidade do objecto (magnitude da velocidade), mas apenas a direcção do vector de velocidade. A força desequilibrada que acelera um objecto pode ser resolvido em um componente que é perpendicular ao percurso, e uma que é tangente ao caminho. Isso produz tanto a força tangencial que acelera o objeto por qualquer diminuir a velocidade ou a acelerar ea força radial (centrípeta), que muda sua direção.
é o unidade vector que aponta no sentido radial para fora a partir do centro. Isto significa que a força centrípeta desequilibrada sentida por qualquer objecto é sempre dirigida para o centro da trajectória curva. Tais forças actuam perpendicularmente ao vector de velocidade associados com o movimento de um objecto, e, portanto, não alteram a velocidade do objecto (magnitude da velocidade), mas apenas a direcção do vector de velocidade. A força desequilibrada que acelera um objecto pode ser resolvido em um componente que é perpendicular ao percurso, e uma que é tangente ao caminho. Isso produz tanto a força tangencial que acelera o objeto por qualquer diminuir a velocidade ou a acelerar ea força radial (centrípeta), que muda sua direção.
Forças fictícias
Há forças que estão dependentes quadro, o que significa que eles aparecem devido à adoção de não-newtoniano (isto é, não-inercial) quadros de referência. Tais forças incluem a força centrífuga e da força de Coriolis. Estas forças são considerados fictícios porque eles não existem em quadros de referência que não estão acelerando. Na relatividade geral , a gravidade se torna uma força fictícia que se coloca em situações onde o espaço-tempo se desvia de uma geometria plana. Como uma extensão, Kaluza-Klein teoria ea teoria das cordas atribuem eletromagnetismo e as outras forças fundamentais, respectivamente, para a curvatura de dimensões diferentemente-escalados, o que, em última análise implica que todas as forças são fictícios.
Rotações e torque de
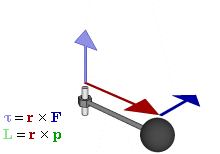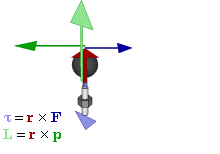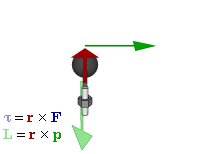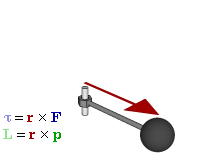
Forças que causam objetos estendidos para rodar estão associados com torques. Matematicamente, o binário sobre uma partícula é definido como o produto cruzado :
onde
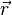 é da partículavector posição em relação a umpivot
é da partículavector posição em relação a umpivot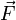 é a força que actua na partícula.
é a força que actua na partícula.
O binário é o equivalente da força de rotação da mesma maneira que o ângulo de rotação é o equivalente de posição, velocidade angular para a velocidade , e o momento angular de impulso . Todos os tratamentos formais das leis de Newton que se aplicavam às forças equivalentemente aplica aos torques. Assim, como consequência da primeira lei do movimento de Newton, existe inércia de rotação que assegura que todos os organismos mantenham seu momento angular, a menos que influenciado por uma de torque desequilibrado. Da mesma forma, segunda lei do movimento de Newton pode ser utilizado para obter uma definição alternativa de torque:
onde
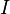 é o momento de inércia da partícula
é o momento de inércia da partícula é a aceleração angular da partícula.
é a aceleração angular da partícula.
Isso proporciona uma definição para o momento de inércia que é o equivalente de rotação para a massa . Em tratamentos mais avançada da mecânica, o momento de inércia actua como um tensor que, quando analisados correctamente, determina completamente as características de rotações incluindo precessão e nutation.
Equivalentemente, a forma diferencial da Segunda Lei de Newton fornece uma definição alternativa de torque:
onde 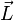 é o momento angular da partícula.
é o momento angular da partícula.
Terceira Lei do Movimento de Newton requer que todos os objetos exercendo torques-se experimentar torques iguais e opostas, e por isso também implica diretamente aconservação do momento angularpara sistemas fechados que experimentam rotações erevoluçõesatravés da ação de torques internos.
Integrais cinemáticas
Forças pode ser utilizado para definir uma série de conceitos físicos por integração no que diz respeito a variáveis cinemáticas . Por exemplo, integrar com respeito ao tempo fornece a definição de impulso:
que, pela segunda lei de Newton, deve ser equivalente à mudança de impulso (obtendo-se oteorema de impulso do impulso).
Da mesma forma, a integração com relação à posição dá uma definição para otrabalho realizadopor uma força:
que, num sistema em que todas as forças são conservadoras ( ver abaixo ) é equivalente a alterações na cinética e potencial de energia (produzindo o teorema de energia de trabalho ). A derivada temporal da definição de trabalho dá uma definição para poder em termos de força e da velocidade ( 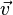 ):
):
Energia potencial
Em vez de uma força, o conceito matematicamente equivalente a um campo de energia potencial pode ser usada por conveniência. Por exemplo, a força da gravidade actua sobre um corpo pode ser visto como a acção do campo gravitacional, que está presente no local do corpo. Restating matematicamente a definição de energia (por definição de trabalho ), um potencial de campo escalar  é definido como aquele campo cuja inclinação é igual e oposta à força produzida em cada ponto:
é definido como aquele campo cuja inclinação é igual e oposta à força produzida em cada ponto:
Forças pode ser classificado como conservador ou não conservativa. As forças conservadoras são equivalentes para o gradiente de um potencial enquanto as forças não conservativas não são.
As forças conservadoras
A força conservadora que atua em um sistema fechado tem um trabalho mecânico associado que permite a energia para converter apenas entre cinéticos ou formas possíveis. Isto significa que, para um sistema fechado, o líquido é conservado a energia mecânica sempre que uma força conservadora actua sobre o sistema. A força, por conseguinte, está directamente relacionada com a diferença em energia potencial entre dois locais diferentes no espaço, e pode ser considerado como sendo um artefato do campo potencial da mesma maneira que a direcção e quantidade de um fluxo de água pode ser considerada ser um artefacto do mapa de contorno da elevação de uma área.
As forças conservadoras incluem a gravidade , a eletromagnética força, ea força da mola. Cada uma destas forças têm modelos que são dependentes de uma posição dada frequentemente como um vector radial 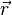 que emana de potenciais esfericamente simétricas. Exemplos deste segue:
que emana de potenciais esfericamente simétricas. Exemplos deste segue:
Para gravidade:
onde 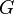 é o constante gravitacional, e
é o constante gravitacional, e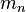 é a massa do objeton.
é a massa do objeton.
Para forças electrostáticas:
onde 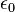 é permissividade elétrica de espaço livre, e
é permissividade elétrica de espaço livre, e é acarga elétricade objeton.
é acarga elétricade objeton.
Para forças de mola:
onde 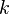 é o constante da mola.
é o constante da mola.
Forças não
Para alguns cenários físicos, é impossível para modelar forças como sendo devido a gradiente de potencial. Este é muitas vezes devido a considerações macrofísicas que as forças de rendimento como resultante de uma média estatística macroscópica de micro. Por exemplo, atrito é causada por os gradientes de numerosos potenciais electrostáticas entre os átomos , mas manifesta-se como um modelo de força que é independente de qualquer vector posição macroescala. Outros do que forças não fricção incluir outras forças de contato, tensão, compressão, e arraste. No entanto, para qualquer descrição suficientemente detalhada, todas essas forças são os resultados de os conservadores desde cada uma dessas forças macroscópicas são os resultados líquidos dos gradientes de potenciais microscópicas.
A conexão entre as forças não-conservadoras macroscópicas e microscópicas forças conservadoras é descrito por tratamento detalhado com mecânica estatística . Em sistemas fechados macroscópicas, forças não actuar para alterar as energias internos do sistema, e são frequentemente associadas com a transferência de calor . De acordo com a Segunda Lei da Termodinâmica , forças não necessariamente resultar em transformações de energia dentro de sistemas fechados de ordenou a condições mais aleatórias como entropia aumenta.
Unidades de medida
O Unidade SI de força é o Newton (símbolo N), que é a força necessária para acelerar uma massa de um quilograma, a uma taxa de um metro por segundo quadrado, ou kg • • m s -2 . O correspondente é a unidade CGS dina, a força necessária para fazer acelerar uma massa de um grama por um centímetro por segundo ao quadrado, ou g • cm • s -2 . 1 newton é, portanto, igual a 100.000 dine.
O foot-pound-segunda unidade imperial da força é a libra-força (lbf), definida como a força exercida pela gravidade sobre uma libra-massa no campo gravitacional padrão de 9,80665 m • s -2 . A força-pound fornece uma unidade alternativa de massa: uma lesma é a massa que vai acelerar por um pé por segundo ao quadrado quando agiu em por um libra-força. Uma unidade alternativa de força no mesmo sistema é o poundal, definida como a força necessária para acelerar uma massa de uma libra de uma taxa de um pé quadrado por segundo. As unidades de lesma e poundal são projetados para evitar uma constante de proporcionalidade na Segunda Lei de Newton .
A força da libra tem uma contrapartida métrica, menos utilizados do que o newton: o quilograma-força (kgf) (às vezes kilopond), é a força exercida pela gravidade padrão em um quilograma de massa. A força-quilograma leva a uma alternativa, mas raramente utilizada unidade de massa: a lesma métrica (às vezes caneca ou H.) é que a massa que acelera a 1 m • s -2 quando submetidos a uma força de 1 kgf. A força-quilograma não é uma parte do moderno sistema SI, e é geralmente obsoleta; no entanto, ele ainda vê usar para algumas finalidades como expressar jet impulso, bicicleta falou tensão, as configurações da chave de torque e torque de saída do motor. Outras unidades arcanas de força incluem o sthène que é equivalente a 1000 N e a Kip que é equivalente a 1000 lbf.
| newton ( Unidade SI) | dina | quilograma-força, kilopond | libra-força | poundal | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg · m / s² | = 105dyn | ≈ 0,10197 mf | ≈ 0,22481lbF | ≈ 7,2330 pdl |
| 1 dyn | = 10-5N | ≡ 1 g · cm / s² | ≈ 1,0197 × 10-6mf | ≈ 2,2481 × 10-6 lbF | ≈ 7,2330 × 10-5pdl |
| 1 mf | = 9,80665 N | = 980.665 dyn | ≡gn· (1 kg) | ≈ 2,2046lbF | ≈ 70,932 pdl |
| 1lbF | ≈ 4.448222 N | ≈ 444.822 dyn | ≈ 0,45359 mf | ≡gn· (1 libra) | ≈ 32,174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 dyn | ≈ 0.014098 mf | ≈ 0.031081lbF | ≡ £ 1 ·ft / s² |
| O valor de gntal como utilizado na definição oficial da quilograma-força é usada aqui para todas as unidades gravitacionais. | |||||